Промер и расчет порошковых рентгенограмм

Промер рентгенограмм может производиться с погрешностью до 0,2 мм с помощью хорошей масштабной линейки. Перед промером линии рентгенограммы нумеруют (чернилами). Цифры следует ставить на краях рентгенограммы, следя за тем, чтобы они соответствовали симметричным по отношению к отверстию линиям. Промер линий должен проходить строго по середине рентгенограммы.

При асимметричной съемке следует сначала найти линии, отвечающие малым и большим углам θ. Линии с малыми углами θ (передние линии) обычно имеют меньшую ширину, чем линии с большими углами θ (задние линии). Для промера цифру 10 на масштабной линейке помещают около отверстия при θ = 0^o и добиваются, чтобы линии с номером 1 рентгенограммы располагались симметрично справа и слева на равном расстоянии от указанного деления. Рентгенограмму закрепляют в этом положении и ведут промер в правую сторону, определяя величины l_изм , а не 2l_изм , как это делается в случае симметричной рентгенограммы.

Более точный промер (с погрешностью до 0,01 мм) может производиться с помощью специального измерительного микроскопа (компаратора). Увеличение этого микроскопа должно быть небольшим (не больше четырехкратного). Пленку по длине располагают параллельно направлению перемещения микроскопа. Визирный крест компаратора должен перемещаться по средней линии рентгенограммы. Отсчеты для данной линии следует делать, приближаясь к ней с обеих сторон.

Порядок расчета рентгенограмм следующий.

1. При симметричной съемке из значений 2l_изм находят угол Вульфа–Брэгга θ по формуле

θ^o = (l_изм/2R)∙57,29.

2. Вносят поправку на поглощение в образце. Положение дифракционных линий на рентгенограмме зависит от прозрачности образца по отношению к падающему пучку рентгеновских лучей.

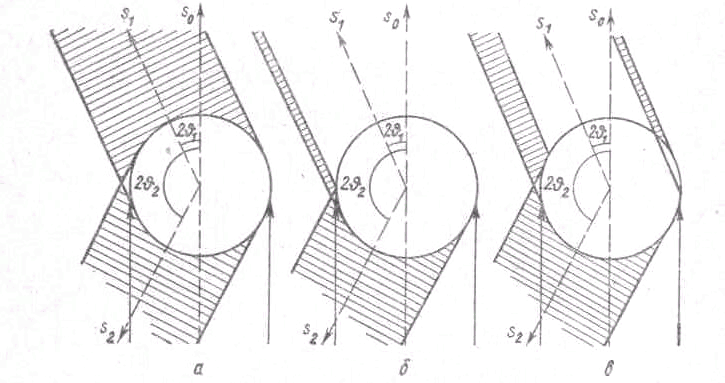
Рис. 5. Ширина линий на рентгенограммах:

а – абсолютно прозрачный образец; б – абсолютно непрозрачный образец;

в – полупрозрачный образец

Если падающий пучок параллелен, а образец абсолютно прозрачен по отношению к нему, то дифракционные линии, как это видно на рис. 5 а, имеют одинаковую ширину при всех углах θ, равную диаметру цилиндрического образца. Если образец абсолютно непрозрачен, то при тех же условиях линии будут иметь различную ширину, уменьшающуюся с уменьшением угла θ (рис. 5 б). Для полупрозрачного образца наблюдается раздвоение линий под небольшими углами θ (рис. 5 в).

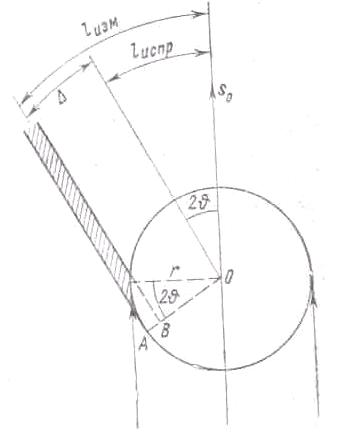
Рис. 6. К выводу поправки на поглощение

Распределение плотности почернения по ширине линии неоднородно, оно зависит от поглощения в образце, его радиуса и брэгговского угла.

Промер расстояний целесообразно проводить между серединами линий, так как они лучше определяются, чем их края. Из-за поглощения середины линий смещаются к большим углам θ, и поэтому из результатов измерений надо вычесть поправку на поглощение Δ:

2l_испр = 2l_изм – 2Δ. (5)

Значение Δ можно найти геометрически, предполагая, что образец абсолютно непрозрачен, а первичный пучок строго параллелен. Из рис. 6 следует, что

Δ = ВО + (АВ/2), ВО = r cos 2θ, AB = AO – BO,

где АО = r (r – радиус образца). Тогда

Δ= ВО + (АО – ВО)/2 = (ВО + А0)/2 = (r/2) (1 + cos2θ) = rcos²θ.

Подставляя значение Δ в выражение (5), получаем

2l_испр = 2l_изм – 2r cos²θ. (6)

Значение Δ, как видно из соотношения (6), уменьшается с увеличением угла θ. Поэтому поправку на поглощение следует учитывать до тех пор, пока она превосходит погрешность измерения. Указанная поправка получена при больших упрощениях, и поэтому ее используют при расчетах рентгенограмм, не связанных с особо точными определениями периодов решетки.

3. Определяют межплоскостные расстояния по формуле

d/n = λ/(2 sinθ). (7)

Если при съемке рентгенограммы применялось неотфильтрованное характеристическое излучение, то предварительно определяют длину волны, относящуюся к данной линии. Для этой цели используют соотношения nλ_α = 2dsinθ_α , nλ_β = 2dsinθ_β.

Отсюда

sinθ_α / sinθ_β = λ_α / λ_β (8)

Кроме того, следует учитывать, что θ_β < θ_α и I_α = 5,5 I_β, где I_α и I_β – интенсивности соответствующих линий характеристического спектра.

После разделения линий на β и α производят расчет межплоскостных расстояний по формулам

d/n = λ_β/sinθ_β , d/n = λ_α/sinθ_α .

Контролем правильности расчета служит попарное совпадение результатов, полученных для линий, обусловленных K_α- и K_β- излучениями.

Часто расчет рентгенограммы (например, при фазовом анализе) заканчивают на этом этапе. Если же стоит задача определения периодов решетки, то рентгенограмма должна быть проиндицирована, т. е. должны быть определены индексы интерференции всех линий, полученных на рентгенограмме.