2.6. Тензор скорости деформации

Деформации линейные и сдвиговые изменяются во времени и для них, как и для любого процесса можно ввести понятие скорости.

Скорости деформации . Здесь - приращение деформации за малый промежуток времени 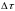. Размерность скорости деформации .

Компоненты тензора скорости деформации можно получить дифференцируя по времени компоненты тензора деформаций . Тензор скорости деформации будем обозначать . Тогда можно записать:

;

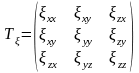. (2.10)

На главной диагонали стоят скорости линейных деформаций - , , . Компоненты характеризуют скорости сдвиговой деформаций ( , , ), то есть скорости изменения углов между материальными волокнами. Тензор симметричный, то есть .

Тензор скорости деформации как любой симметричный тензор имеет главные скорости относительных удлинений , , , а также три взаимно перпендикулярных вектора, называемых направлениями главных скоростей удлинений.

Индексация главных скоростей удлинений (главных скоростей деформации) принята такой, что .

Тензор скоростей деформаций в главных скоростях деформации:

.

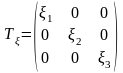Эта запись означает, что деформацию материала в любой точке в единицу времени можно представить удлинением или укорочением по трем взаимно перпендикулярным направлениям главных скоростей деформации. На рис. 2.8 показан элементарный параллелепипед, ребра которого совпадают с направлениями главный скоростей деформаций.

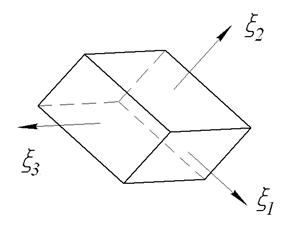
Рис. 2.8. Элементарный параллелепипед, ребра которого совпадают с

направлениями главный скоростей деформаций

Порядок определения главных скоростей деформаций и их направлений аналогичен описанному ранее для напряжений и деформаций: по матрице (2.10) составляют инварианты

Инварианты являются коэффициентами характеристического уравнения:

.

Максимальный из корней уравнения будет , минимальный , средний - . Для определения направлений главных скоростей необходимо решить систему:

.

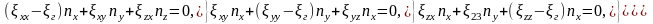Подставив вместо значение , определим направляющие косинусы ^{, определяющие положение главной оси 1. Подставив вместо} значение , определим 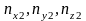и т. д.

2.7. Разложение тензора скорости деформации на шаровой тензор и девиатор

Тензор скоростей деформаций можно разложить на 2 тензора: шаровой тензор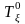 и девиатор [4]:

;

.

Компоненты девиатора скорости деформации можно записать в виде:

.

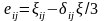Тогда компоненты тензора скорости деформации :

.

Шаровой тензор характеризует скорость изменения объема, а девиатор - скорость изменения формы.

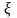- скорость относительного изменения объема:

.

- скалярная характеристика скорости деформации в точке.

Для несжимаемого материала:

.

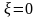Тогда компоненты тензора скорости деформации и девиатора совпадают, то есть:

.

Известным образом можно записать инварианты : ; ; . Важной скалярной характеристикой скорости деформации в точке является интенсивность скоростей деформации сдвига:

;

.

В тензорной записи: .

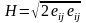Если тензор задан в главных направлениях:

.

Тогда: .

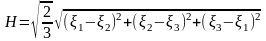Приращение деформации сдвига на малом этапе деформации за малый промежуток времени ( <0,1 c):

. (2.11)

Нас интересует вся пластическая деформация, накопленная материальной частицей, то есть степень деформации сдвига:

,

где n – количество этапов деформации.

При предельном переходе (при n→ ) с учетом (2.11) получим:

. (2.12)

Формула (2.12) позволяет определить всю накопленную материальной частицей деформацию за время деформирования . Интеграл в (2.12) вычисляется вдоль траектории движения материальной частицы. На малом этапе деформации .