
- •2. Теория деформаций
- •2.1. Определение линейной и сдвиговой деформации. Различные меры линейной деформации
- •2.2. Деформированное состояние точки. Тензор малых деформаций
- •2.3. Главные оси тензора деформаций. Главные деформации
- •3.4. Шаровой тензор и девиатор деформаций
- •2.5. Связь между перемещениями и малыми деформациями (геометрические уравнения)
- •2.6. Тензор скорости деформации
- •2.7. Разложение тензора скорости деформации на шаровой тензор и девиатор
- •2.8. Кинематические уравнения
- •2.9. Кинематически возможное поле скоростей в трубе, находящейся под действием внутренним давления
2. Теория деформаций
2.1. Определение линейной и сдвиговой деформации. Различные меры линейной деформации
Деформация – это изменение размеров тела. Если под действием сил произошло изменение хотя бы одного размера, то произошла деформация.
Если в деформируемом
теле имеется материальное волокно до
деформации длиной
 ,
то после деформации оно будет иметь
длину
,
то после деформации оно будет иметь
длину
 (рис. 2.1).
(рис. 2.1).

а) б)
Рис. 2.1. Материальное волокно до (а) и после (б) деформации
Абсолютная
линейная деформация – это величина,
определяемая по формуле:
 .
.
Линейная деформация характеризует только изменение размера одного волокна и не описывает изменение положения волокна.
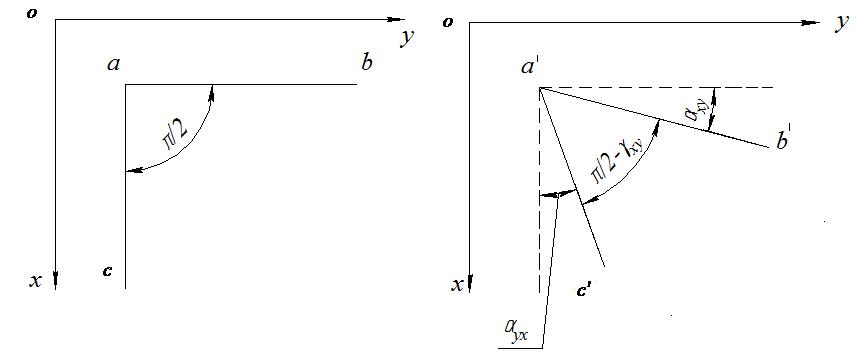
В качестве меры линейной деформации используют относительную деформацию:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ,
,
где
 и
и
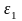 -
относительная деформация;
-
относительная деформация;
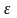 - истинная или логарифмическая
деформация.
- истинная или логарифмическая
деформация.
Связь между различными мерами деформации:
 ;
;
 ;
;
 ;
;
 .
.
Для малых деформаций (меньших 0,1) безразлично, какой выбирается мера.
Логарифмическая мера деформации обладает свойством аддитивности [5]. То есть если деформацию разбить на этапы, то деформацию на этапах можно складывать:
 .
.
Для других мер деформации:
 .
.
Покажем это,
рассмотрев три этапа деформации
материального волокна, с исходной длиной
 :
:
 .
.
Мера – логарифмическая деформация (или истинная):
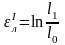 ;
;
 ;
;
 ;
;
 .
.
 .
.
Мера – относительная деформация:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Сдвиговая деформация (деформация сдвига) характеризует изменение положения двух пересекающихся волокон. Пусть два волокна до деформации взаимно перпендикулярны, а после деформации угол стал тупым (рис. 2.2).
Мера сдвиговой
деформации – изменение угла между
волокнами (угол
 на рис. 2.2).
на рис. 2.2).
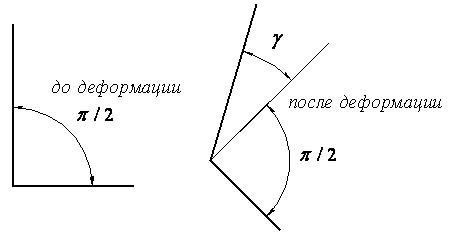
Рис. 2.2. Сдвиговая деформация
2.2. Деформированное состояние точки. Тензор малых деформаций
Деформированное состояние в точке характеризуется линейными деформациями всех волокон и сдвигами во всех плоскостях, проходящих через данную точку.
Для задания деформированного состояния в точке достаточно задать линейную деформацию трех волокон и сдвиги в трех плоскостях, проходящих через данную точку.
Для удобства выберем линейные деформации трех волокон, совпадающих с координатными осями x, y, z и сдвиги в трех координатных плоскостях xoy, xoz и yoz (рис. 2.3).
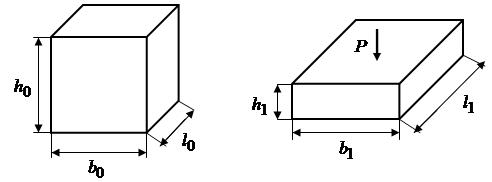
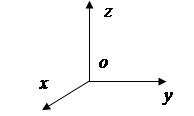
а)
б) в)
Рис. 2.3. Принятая система координат (а) и схема деформирования материальной частицы (б и в – частица соответственно до и после деформации)
Показанная на рис.
2.3 частица деформируется таким образом,
что углы между ребрами не изменяются,
а изменяются только длины ребер. В этом
случае линейные деформации
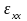 ,
,
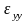 ,
,
 можно
рассчитать по формулам
можно
рассчитать по формулам
 ,
,
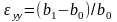 ,
,
 ,
,
а сдвиговые
деформации будут равны нулю. Отметим,
что условие сохранения объема частицы
выражается равенством
 .
.
Сдвиги
 будем обозначать двумя индексами,
указывающими в какую координатную
плоскость проецируется искаженный
деформацией угол. На рис. 2.4 показаны
волокна до (ac и ab)
после (
будем обозначать двумя индексами,
указывающими в какую координатную
плоскость проецируется искаженный
деформацией угол. На рис. 2.4 показаны
волокна до (ac и ab)
после ( и
и
 )
деформации. В этом случае сдвиговая
деформация рассчитывается по формуле
)
деформации. В этом случае сдвиговая
деформация рассчитывается по формуле
 ,
,
где
 и
и
 - углы в радианах.
- углы в радианах.
а) б)
Рис. 2.4. Положение волокон до (а) и после деформации (б)
При определении
деформации безразлично какими будут
относительные значения углов
и
,
лишь бы их сумма была
 .
Это дает возможность каждую компоненту
сдвиговой деформации представить в
виде суммы двух углов и рассматривать
половины значений
.
Таким образом, будем брать
.
Это дает возможность каждую компоненту
сдвиговой деформации представить в
виде суммы двух углов и рассматривать
половины значений
.
Таким образом, будем брать
 ,
,
 ,
,
 .
Индексация
будет
совпадать с индексацией касательных
напряжений
.
Индексация
будет
совпадать с индексацией касательных
напряжений
 .
.
Деформированное состояние в точке характеризует таблица:
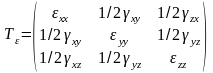 ,
,
называемая тензором малых деформаций. Другое обозначение:
 .
.
