22. Теорема о среднем.

Теорема 8. Пусть f : X → , X €Rⁿ, где X - область. Пусть отрезок [x; x + h] с концами x,x + h содержится в X. Если функция f непрерывна в точках отрезка [x; x + h] и дифференцируема в точках интервала (x; x + h), то найдется такая точка 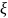€ (x; x + h), что имеет место равенство f (x + h) — f (x) = f '( )h.

Доказательство. Рассмотрим вспомогательную функцию F(t) = f (x + ht), определенную на отрезке 0 <=t <=0 Функция F удовлетворяет всем условиям теоремы Лагранжа: она непрерывна на [0; 1], как композиция непрерывных отображений, и дифференцируема в интервале (0; 1) , как композиция дифференцируемых отображений. Следовательно, найдется точка в 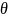€ (0; 1), такая, что F(1) — F(0) = F'( ) 1. Но F(1) = f (x + h), F(0) = f (x), F'( ) = f'(x + h)h, что и означает справедливость теоремы.□ Из теоремы 8 вытекает Следствие 1. Если функция f : X → , X € ⁿ дифференцируема в области X, и в любой точке x € X ее диффе­ренциал равен нулю, то f постоянна в области X.

23.Формула Тейлора для функций многих переменных.

Введем обозначения .

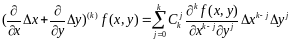Теорема1.Пусть ф-ция z=f(x,y) непрерывна вместе со своими частными производными до n-го порядка включ. в некот. 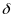окрестности 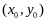, тогда для 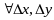удовлетворяющих условию 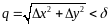сущ. такое 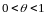, что 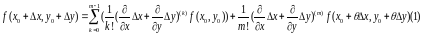Эта фор-ла назыв. формулой Тейлора с остаточным членом в форме Лагранжа.

Замечание: в условии Т1 имеет место ф-ла

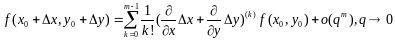
Эта ф-ла Тейлора с остаточным членом в форме Пеано. Замечание: в случае m=1 , ф-ла (1) имеет вид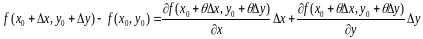 и назыв. конечным приращением Лагранжа для ф-ции 2-ух переменных. Аналогично опред. ф-ла Тейлора для функций многих переменных.

24. Необходимые условия экстремума.

Определение 1. Пусть функция f(x) определена на множестве X С Rⁿ. Точка a € X называется точкой локального максимума (минимума) функции f, если существует окрестность V(a) такая, что для всех x € V(a) выполняется неравенство f (x) <=f (a) (f (x) >= f (a)).

Если для x € V(a) имеет место неравенство f(x) < f(a)( f (x) > f(a)), то точка a называется точкой строгого локального максимума (минимума) функции f.

Определение 2. Точки локального максимума и минимума функции f называются точками локального экстремума функции f, а значения функции в этих точках называются локальными экстремума функции.

Теорема 10. Пусть функция f определена в окрестности V(a) С Rⁿ точки a, имеет в точке a частные производ­ные по каждой из переменных x ₁, . . . , x_n. Тогда для того, чтобы функция f имела в точке a локальный экстремум, необходимо, чтобы в этой точке были выполнены равенства 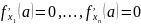.(6.24)

Точки, в которых выполнены условия (6.24), называются стационарными точками функции f.

Следовательно, если функция f имеет в точке a локальный экстремум, то точка a является стационарной точкой функции f или функция f в этой точке не дифференцируема.

25. Достаточные условия локального экстремума.

При формулировки достаточного условия играет важную роль второй дифференциал в точке 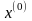. Квадратичная форма A(x) = , , 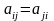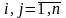(1)

Квадратичная форма называется положительно (отрицательно) определенной, если для любого 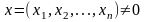выполняется неравенство: ( ).

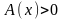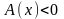Положительно и отрицательно определенные квадратичные формы наз. знакоопределенными.

Квадратичные формы принимающие как положительные, так и отрицательные значения наз. знаконеопределенными (знакопеременными).

Т1(Достат. условие экстремума.): Пусть функция 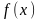, где 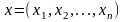дважды дифференцируема в окрестности своей критической точки 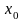. Тогда если второй дифференциал : 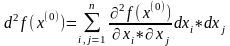является положит(отриц) квадратичной формой, то точка является точкой строгого минимума(максимума). Если второй диффер знакоперем квадрат форма, то в т. экстремума нет.

Замечание: Для установления знакоопред квадр формы сущ критерий Сильвестра, а именно для того, чтобы квадр форма (1) была положит опред необх и дост, чтобы:

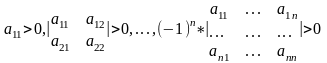
а для того, чтобы квадр форма (1) был отр опред необх и дост, чтобы знаки чередовались:

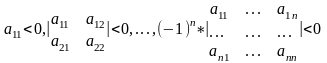
Сформ Т1 для случая двух переменных.

Т2: Пусть ф-ция 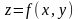опред и имеет непрер частные произв 2-ого порядка в некототой окрестн т. 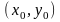, каторая явл критическо для ф-ций . Т.е. в ней .

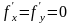Тогда если в т. 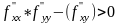, она явл точкой строгого экстрем, а именно строгого максим, если 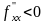( 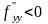) и миним, если 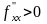( 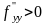). Если же в т. 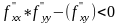, то экстрем в ней нет.

Если 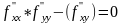, то может случится, что экстрем есть или нету.