
- •1.Несобственные интегралы и их свойства.
- •2. Критерий Коши сходимости несобственных интегралов.
- •5. Неравенство Коши.
- •6. Метрическое пространство .
- •7.Евклидово пространство .
- •8. Последовательности точек пространства .
- •9. Предел отображения.
- •10. Предел по направлению. Повторные пределы.
- •11. Непрерывность отображения в точке.
- •12.Глобальные свойства непрерывных отображений.
- •13. Линейные отображения.
- •14. Дифференцируемые отображения.
- •15. Дифференциал и частные производные функции многих переменных.
- •16. Координатное представление дифференциала отображения. Матрица Якоби.
- •18 Достаточное условие дифференцируемости функций многих переменных.
- •19.Производная по направлению. Градиент.
- •20. Частные производные высших порядков.
- •22. Теорема о среднем.
- •23.Формула Тейлора для функций многих переменных.
- •24. Необходимые условия экстремума.
- •25. Достаточные условия локального экстремума.
- •26. Неявные функции.
- •27. Обратное отображение.
- •28. Необходимые условия зависимости функций.
- •29. Достаточные условия зависимости функций.
- •31. Метод множителей Лагранжа.
- •32. Достаточный признак условного экстремума.
- •33. Абсолютный экстремум.
- •34. Понятие числового ряда и свойства сходящихся рядов.
- •35. Признаки сравнения сходимости числовых рядов.
- •36. Признаки Даламбера и Коши сходимости рядов.
- •37. Интегральный признак сходимости ряда.
- •38. Знакочередующиеся ряды.
- •39.Абсолютно и условно сходящиеся ряды.
- •40. Признак Абеля и Дирихле.
- •41. Перемножение абсолютно сходящихся числовых рядов.
- •42. Бесконечные произведения.
8. Последовательности точек пространства .
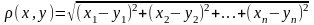 -расст.
м/д x
и y.
Опр1.Пусть
х€Rn
, ε>0.
Совокупность всех таких точек у€Rn
, что ρ(х,у)<
ε наз. n-мерным
открытым шаром, радиуса ε, с центром в
точке х или ε -окрестностью(сферической
или шаровой) в т. х пр-ва Rn
и обознач-ся
U(x,
ε).
-расст.
м/д x
и y.
Опр1.Пусть
х€Rn
, ε>0.
Совокупность всех таких точек у€Rn
, что ρ(х,у)<
ε наз. n-мерным
открытым шаром, радиуса ε, с центром в
точке х или ε -окрестностью(сферической
или шаровой) в т. х пр-ва Rn
и обознач-ся
U(x,
ε).
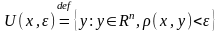
Опр2.
Мн-во P(x,δ1,…,
δn
)={y=(
y1
, y2
,…, yn):
|xi
–yi
|<δi
 i=1,2,…n}
наз. прямоугольной
окр-стью т.х.
i=1,2,…n}
наз. прямоугольной
окр-стью т.х.
В частности, если δ1 =δ2 =…=δn =δ , то мн-во Р(х, δ)=def= P(x,δ,…, δ ) наз. кубической окрестностью т.х.
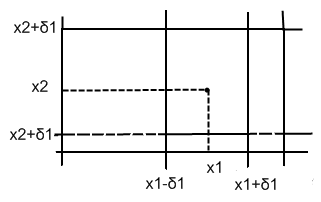 Очевидно,
что если δ0
=min
(δ1,…,
δn
), a
δ
=max
(δ1,…,
δn
), то
P(x,δ0)
Очевидно,
что если δ0
=min
(δ1,…,
δn
), a
δ
=max
(δ1,…,
δn
), то
P(x,δ0)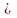 P(x,δ1,…,
δn
)
P(x,δ).
P(x,δ1,…,
δn
)
P(x,δ).
Лемма. Любая сферич. окр-сть т-ки пр-ва Rn содержит прямоуг. окр-сть и содержится в прямоуг. окр-сти этой точки.И наоборот, любая прямоуг. окр-сть т-ки содержит сферич. окр-сть и содержится в сферич.
Если из некот. членов посл-ти { x(n)} сост. новая посл-ть {x(mk) },в кот. порядок следования её членов совпадает с порядком след-ния их в исх. посл-ти, то посл-ть {x(mk) } наз. подпоследовательностью п-сти {x(n)}.
Опр3.
х€Rn
наз. пределом
посл-ти x(m)
€Rn
, если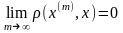 .
В этом случае пишут
.
В этом случае пишут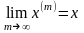 :
и говорят, что посл-ть {x(m)}
сходится в т. х. Посл-ть, которая сходится
к нек-ой т-ке наз. сходящ-ся.
:
и говорят, что посл-ть {x(m)}
сходится в т. х. Посл-ть, которая сходится
к нек-ой т-ке наз. сходящ-ся.
Теорема1. Для того чтобы посл-ть x(m) = (x1(m) , x2(m) ,…, xn(m) ) имела своим пределом т.х=(x1 , x2 ,…, xn ) необх. и дост. чтобы limm→∞ xi(m) = xi , i=1,2…n.
Док-во:
Это утвержд.
сразу след. из нер-ва
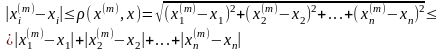
Из т1 след., что если послед имеет предел, то он единственный.
Всякая подпосл. сход-ся к тому же пределу, что и исх. послед.
Опр4.
Послед. {x(m)},
x(m)
€R
называется фундамент-ой, если
ε>0
 m0€N
такой, что
m>m0
и
p€N
выполн.
m0€N
такой, что
m>m0
и
p€N
выполн.
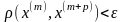 . Следов, чтобы послед. была сход., необх.
и дост. чтобы она была фундамент.(Критерий
Коши)
. Следов, чтобы послед. была сход., необх.
и дост. чтобы она была фундамент.(Критерий
Коши)
Опр5. Мн-во в n-мерном пр-ве наз. ограниченным, если оно сод-ся в некотором n-мерном кубе.
Опр6. Послед. точек пр-ва Rn назыв. огран., если мн-во их значений ограничено.
Теорема2. Из любой огран. посл-ти точек n-мерного пр-ва можно выделить сход-ся подпосл-ти.
Опр7. ε-окр-стью бескон. удалённой т-ки, т.е. U(∞, ε), наз. мн-во сост. из всех таких точек х, что ρ(х,0)> 1/ ε и беск. удал. т-ки.
Опр8. Посл-ть {x(m)} наз. посл-стью стремящейся к ∞, если limm→∞ ρ(x(m) ,0)=+∞.
9. Предел отображения.
Будем рассматривать отображение f : X — Rm, где X € Rn. Возможны случаи: Если m = п =1, то f — функция одной переменной; Если m = 1,п > 1, то f — функция многих переменных; Если m > 1 , п = 1 , то f — вектор функция;
Если m > 1 , п > 1 , то f — отображение
Запись
y
=
f
(x)
—
подразумевает,
x
=
(x1
,
x2,
.
.
.
,
xn),
y
=
(y1
,
y2,
.
.
.
,
ym),
f
= (f1
,
f2,
.
.
.
,
fm).
Отметим,
что функции yi
= fi(x),
i
=
1,m
от
п
переменных
называют координатными функциями
отображения f.
Расстояния в метрических пространствах
Rn
и
Rm,
будем
обозначать соответственно:
pn(x,
a)
=
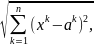 pm(y,b)
=
pm(y,b)
=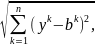
где x, a €Rn, y, b €Rm.
Отображение f : X — Rm, где X € Rn называется ограниченным на X, если f (X) € Rm ограниченно в Rm. Пусть f : X — Rm, где X € Rn, a — предельная точка множества X.
Определение
1.
Точка
b
€Rm
называется
пределом отображения f
в
точке a,
если для любого
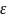 > 0 существует
> 0 существует
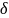 > 0 такое,
что для любого x
€
X
и
0
< pn(x,a)
<
следует, что pm
(f
(x),
b|
<
.
При
этом пишут lim
f
(x)
= b.(x→a).
> 0 такое,
что для любого x
€
X
и
0
< pn(x,a)
<
следует, что pm
(f
(x),
b|
<
.
При
этом пишут lim
f
(x)
= b.(x→a).
Определение 2. Точка b € Rm называется пределом отображения f в точке a, если для любой окрестности U(b) существует V(a) такая, что если x €V(a) ∩X, то f (x) €U(b).
Определение 3. Точка b G Rm называется пределом отображения f в точке a, если для любой последовательности x(k) € X\{a}, k = 1, 2,... сходящейся к точке a, последовательность {f (x(k))} сходится к точке b.
Эквивалентность определений 1 и 2 доказывается аналогично случаю функции одной переменной.
Теорема 3. Точка b = (b1, .. ., bm) является пределом отображения f : X — Rm, X € Rn при x → a тогда и только тогда, когда lim fi(x) = bi, i = 1,m.(x—>a)
Теорема 4. Отображение f : X →Rm, X С Rn имеет предел в точке a тогда и только тогда, когда
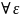 >
0
>
0
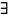 V(a)
:
х',
x"
€
V(a)→
pm
(f(x1),
f (x")) <
.
V(a)
:
х',
x"
€
V(a)→
pm
(f(x1),
f (x")) <
.
Теорема 5. Если отображение f : X — Rm, где X € Rn имеет предел в точке a, то:
предел единственный;
отображение f ограниченно в некоторой проколотой окрестности V(a) точки a в множестве X.
Теорема 6. Пусть f : X → Rm, g : X → Rm, где X € Rn, и существуют пределы lim f (x) = b(x→a), lim g(x) = c(x→a). Тогда существуют пределы:
1) lim (f (x) ± g(x))= b ± c; (x→a)
2) lim f(x) . g(x) = b . c, (x→a)
где f ± g, b ± c — есть сумма и разность векторов; f • g, b • c — скалярное произведение векторов.
Теорема 7. Пусть f : X — R, g : X — R, X € Rn, и существуют пределы lim f(x) = A(x→a), lim g(x) = B. (x→a) Тогда существуют пределы:
1) lim( f (x) ± g(x)) = A ± B,
x— a
2) lim f(x)g(x) = A • B,
x— a
3) если
g(x)
≠
0,
x
€ V(a)
и
B
≠
0,
то
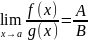 .
.
Замечание 1 . Заметим, что вначале мы говорим, что существуют пределы отображений f и g, а только после этого можем говорить о существовании предела f ± g и f • g.
Замечание 2. Для пределов функций многих переменных справедливы и другие свойства аналогичные свойствам функций одной переменной, при этом формулировки теорем и их доказательства по существу остаются теме же самыми.
