1.Несобственные интегралы и их свойства.

Опр.: Пусть ф-ция определена на промежутке и интегрируема на любом отрезке содержащемся в этом промежутке. Величина называется несобственным интегралом Римана от ф-ции по промежутку (НИ-1)

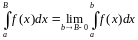Опр.: Пусть ф-ция определена на промежутке и интегрируема на любом отрезке . Величина называется несобственным интегралом от ф-ции по промежутку (НИ-2)

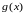Теорема 1: Пусть и функции определенные на промежутке , интегрируемы на любом отрезке , и для них определены несобственные интегралы .

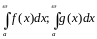Тогда 1) Если и , то значения интеграла понимаемого как в несобственном, так и в собственном смысле, совпадают.

2)При любых функция интегрируема в несобственном смысле на и справедливо равенство

3) Если 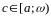, то

4) Если - гладкое, строго монотонное отображение, причем и при , то несобств. интеграл от функции существет и справедливо равенство

Теорема 2. Если f,g €Cⁱ[a; w) и существует предел lim(f(x)•g(x))(x→w), то функции f•g' и f'•g одновременно интегрируемы или не интегрируемы в несобственном смысле на [a; w) и в случае интегрируемости справедливо равенство

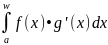^{= f (x)•g(x)|wa - ,} где f(x) • g(x)|^w_a = lim f (x)•g(x) - f(a)•g(a) (x→w).

2. Критерий Коши сходимости несобственных интегралов.

Сходимость несобственного интеграла равносильна существованию предела функции

при

Теорема: Если функция определена на промежутке и интегрируема на любом отрезке , то интеграл сходится тогда и только тогда, когда для любого 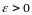можно указать так, что при любых таких, что 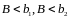, имеет место соотношение

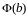Д оказательство: Поскольку , то выписанное условие есть критерий Коши существования предела функции при

3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости НИ. Опр.: Несобственный интеграл (1) называется абсолютно сходящимся, если сходится интеграл (2). Функции, для которых интеграл абсолютно сходится, называются абсолютно интегрируемыми на промежутке с концами

Теорема: Абсолютно сходящийся несобственный интеграл является сходящимся.

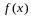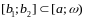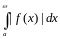Доказательство. Ввиду того, что задан несобственный интеграл (1), сужение функции интегрируемо по Риману на любом отрезке . Отсюда по св-ву модуля определенного интеграла устанавливаем, что . Несобственный интеграл сходится. Тогда по критерию Коши сходимости несобственного интеграла

Из приведенных выше соотношений по критерию Коши следует, что несобственный интеграл сходится.

Следствие 1: Если НИ (1) расходится, то расх и НИ (2).

Опр: Если НИ (1) сходится, а НИ (2) расх, то НИ (1) наз-ся условно сходящимся.

Теорема 5. Если функция f (x) определена на [a;w), интегрируема на каждом отрезке [a; b] €[a; w) и f (x)>=0 на [a;w), то несобственный интеграл (1) сходится тогда и только тогда, когда функция ограничена [a; w).

Доказательство. Действительно, если f (x) >= 0 на [a; w), то функция неубывающая на [a; w) и потому она имеет предел при b → w, b € [a; w) если и только если она ограничена. □

Теорема 6 (признак сравнения). Пусть функции f (x), g(x) определены на промежутке [a; w), неотрицательны и интегрируемы на любом отрезке [a; b] € [a; w). Если функция f(x) ограничена по сравнению с функцией g(x) при x → w, то:

а) из сходимости интеграла (3)следует сходимость интеграла 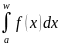(4);

б) из расходимости интеграла следует расходимость интеграла .

Следствие 2 (предельный признак сравнения). Пусть функции f(x), g(x) неотрицательны на полуинтервале [a; w), g(x) ≠ 0 для любого x€[a; w) и существует

Тогда:

а) если интеграл (3)сходится и 0<= к < +oo, то интеграл (4) также сходится;

б) если интеграл (3) расходится и 0 < к <= +oo, то интеграл (4) также расходится.

В частности, если f (x) и g(x) эквивалентные при x → w функции, то интегралы (3) и (4) сходятся или расходятся одновременно.

4. Достаточное условие сходимости.

Признак Дирихле.

Теорема: Пусть:

1. функция непр. и имеет ограниченную первообразную 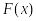при ;

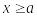2. функция непр. дифференцируема и убывает при ;

3. 

Тогда сходится интеграл

Доказательство: Заметим, что ф-ция непрерывна, а значит и интегрируема по Риману на любом отрезке .

Проинтегрировав по частям произведение на [a;b], получим (1)

Исследуем правую часть при 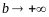. В силу ограниченности функции M=sup|F(x)|< . Из условий 2 и 3 следует, что функция не отрицательна для всех _{, в частности , поэтому , кроме того в силу условия 3, . Далее из убывания ф-ции} следует, что при _{, поэтому}

Таким образом, интегралы ограничены в совокупности при всех , поэтому интеграл сходится абсолютно, а значит и просто сходится, т.е. существет конечный предел Итак, доказали, что в правой части рав-ва (1) оба слагаемых при имеют конечный предел, значит предел левой части тоже конечен.

Признак Абеля

Теорма: Если на

1. Ф-ция непрерывна и сходится интеграл

2. функция непрерывно дифференцируема, ограничена и монотонна, то интеграл сходится.

Доказательство: Отметим, что интегралы и сходятся и расходятся одновременно и что в силу монотонности одна из функций или убывает.

Пусть для определенности, убывает функция . В силу ее ограниченности и монотонности, существует конечный предел

, а т.к. ф-ция убывает, то при 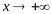, убывая стремится к нулю и разность 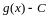. Представим произведение в виде В силу сходимости , интеграл также сходится. Из этого условия следует, что интегралы , ограничены. В самом деле, из существования конечного предела следует ограниченность ф-ции 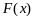в некот. окресности 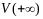. На отр-ке ф-ция огр., т.к. она непрерывна. В рез-те ограничена на всей полупрямой 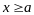. Ф-ция явл. первообразной ф-ции , тем самым ф-ция имеет первообразную при

Значит интеграл сходится.