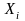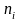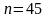- •Глава 14 Расчётное задание по тв и мс
- •14.1 Варианты расчётного задания
- •Вопросы к экзамену
- •Задачи для подготовки к экзамену
- •Приложения Приложение а. Буквы греческого алфавита
- •Приложение б. Основные законы распределения
- •Приложение в. Таблицы математической статистики
- •Приложение г. Набор данных
Глава 14 Расчётное задание по тв и мс
14.1 Варианты расчётного задания
Расчётное задание состоит из 4 задач.
Условия задач 1 – 2 указаны в каждом варианте. Задания предлагаются по следующим темам.
Исследовать дискретную выборочную совокупность.
Исследовать непрерывную выборочную совокупность.
Условие задачи 4 общее для всех, отличаются лишь экспериментальные данные.
На основании таблицы значений располагаемого личного дохода (Х) населения США и текущих расходов (Y) (в каждом варианте указана статья расходов) за 25-летний период с 1959 по 1983 гг. найти:
а) выборочные средние для Х и Y;
б) выборочную ковариацию между Х и Y;
в) выборочные дисперсии для Х и Y;
г) выборочный коэффициент линейной корреляции между Х и Y и пояснить полученное значение;
д) уравнение линейной регрессии Y на X;
е) коэффициент детерминации и объяснить его смысл;
построить:
а) корреляционное поле;
б) график линейной регрессии Y на X (на одном графике с корреляционным полем).
Вариант 1
Имеются данные 70 обследований о производстве стали за месяц на одном из заводов (т):
850,880,910,920,950,920,910,850,920,860,910,950,960,920,850,880,850,920,910,920,860,910,950,920,880,920,880,910,910,920,950,880,850,870,910,880,950,920,850,870,950,860,910,850,860,910,880,850,920,850,880,910,920,950,920,910,920,950,880,850,860,870,910,880,950,920,850,880,910,920.
Сгруппировать выборку, построить полигон частот. Найти моду, медиану, выборочную среднюю и выборочную дисперсию. Определить процент, какой составляют: а) 850 т стали; б) 920-960 т стали среди данных обследования.
Имеются следующие данные о распределении рабочих по стажу работы:
Стаж работы в годах |
До 1 |
1-3 |
3-5 |
5-10 |
более 10 |
Итого |
Число рабочих |
10 |
40 |
80 |
100 |
20 |
250 |
Построить гистограмму частот. Какая часть рабочих предприятия имеет стаж: а) не более 3-х лет; б) свыше пяти лет. Выразить в процентах. Найти моду и медиану.
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на лекарства за 25-летний период с 1959 по 1983 гг.
Вариант 2
Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:
5,1,4,5,4,3,5,5,2,5,6,6,4,3,1,5,2,5,5,5,3,3,3,6,6,5,6,5,3,4,5,4,6,6,5,2,1,5,4,5,5,3,6,4,5,5,4,3,5,5,5,4,5,6,1,5,2,6,4,4,3,5,6,3,5,6,2,5,4,5,5,4,6,5,2,5,3,4,5,6,5,5,3,5,4,6,6,5,5,4,5,5,6,5,6,5,5,6,5,5.
Определить процент рабочих, имеющих: а) 4-ый разряд; б) 5-ый разряд. Сгруппировать выборку, построить полигон частот. Найти моду, медиану и выборочную среднюю.
Обследование электрических лампочек по сроку их службы на повышенном напряжении представлено таблицей.
-
Срок службы (в час.)
Число лампочек, перегоревших в течение данного срока
0 – 50
50 – 100
100 – 150
150 – 200
200 – 250
250 - 300
2
20
48
60
42
28
Итого
200
Построить гистограмму частот. Найти выборочную дисперсию и выборочное среднее квадратичное отклонение, взяв в качестве вариант середины интервалов. Найти моду и медиану.
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на местный транспорт за 25-летний период с 1959 по 1983 гг.
Вариант 3
На городской телефонной станции провели 50 наблюдений средней продолжительности одного телефонного разговора (мин):
3,4,5,3,3,5,2,6,4,7,10,5,3,3,2,4,3,2,4,5,16, 10,12,13,3,4,13,10,6,4,5,2,7,10,15,3,3,4,2,5,7, 10,5,10,3,4,5,10,15,10.
Сгруппировать выборку, построить полигон частот. Найти моду, медиану, выборочную среднюю и выборочную дисперсию. Определить процент продолжительности одного телефонного разговора (мин): а) менее 3 мин; б) больше 5 мин.
Через каждый час измерялось напряжение тока в цепи. При этом были получены следующие значения (в вольтах):
-
227
229
215
230
232
219
222
221
227
226
220
216
220
221
224
223
220
218
222
226
209
212
207
219
220
211
215
218
219
220
Построить интервальный вариационный ряд (первый интервал [210;215). Построить гистограмму частот, найти выборочную среднюю, взяв в качестве вариант середину интервала. Насколько часто напряжение тока в цепи было в пределах от 216 до 220 вольт (выразить в процентах)? Найти моду и медиану
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на одежду за 25-летний период с 1959 по 1983 гг.
Вариант 4
Построить дискретный вариационный ряд и начертить полигон распределения 60 абитуриентов по числу баллов, полученных ими на приемных экзаменах:
-
20
19
22
24
21
18
21
24
21
18
23
21
17
22
20
16
22
18
20
21
18
22
23
21
21
19
22
21
19
20
23
17
20
16
15
23
19
20
24
21
20
18
20
17
21
17
19
20
25
23
20
19
24
23
22
25
21
23
21
24
Найти средний балл при поступлении. Чему равны мода и медиана? Сколько абитуриентов (в процентах) получили не менее 20 баллов на экзамене?
Имеются данные обследования 200 проб нитей на их крепость:
Крепость нити (г) |
120-130 |
130-140 |
140-150 |
150-160 |
160-170 |
170-180 |
180-190 |
190-200 |
Итого |
Число проб |
1 |
8 |
27 |
58 |
56 |
34 |
14 |
2 |
200 |
Построить гистограмму частот. Найти среднюю крепость нити, взяв в качестве вариант середины интервалов. Найти выборочную дисперсию и выборочное среднее квадратичное отклонение, моду и медиану.
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на воздушный транспорт за 25-летний период с 1959 по 1983 гг.
Вариант 5
Обследовано 110 семей сотрудников института, причём зарегистрировано следующее количество детей в семьях:
1,2,2,2,0,1,2,2,1,1,1,0,0,0,1,1,2,2,1,1,1,1,1,1, 2,1,1,2,3,3,1,3,1,0,0,1,1,0,1,1,0,3,0,1,3,1,1,2, 1,1,3,2,2,2,2,2,2,2,2,2,2,2,0,2,1,2,0,2,2,3,3,2, 2,2,0,1,3,2,2,1,2,2,2,1,3,1,2,1,2,2,3,2,0,1,2,1, 0,2,1,1,1,0,1,2,1,0,0,1,1,0.
Сгруппировать выборку, построить полигон частот. Найти моду, медиану и выборочную среднюю и выборочную дисперсию. Определить процент семей, у которых: а) нет детей; б) 3 детей.
Сорок наблюдений за жирностью молока дали такие результаты (%):
3.85 |
4.06 |
3.67 |
3.97 |
3.76 |
3.69 |
3.76 |
3.71 |
3.98 |
3.57 |
3.87 |
4.07 |
3.99 |
4.03 |
4.14 |
3.72 |
3.52 |
3.89 |
4.17 |
3.92 |
4.26 |
4.01 |
3.93 |
3.71 |
3.76 |
4.00 |
3.46 |
4.08 |
3.88 |
3.73 |
3.94 |
3.82 |
4.17 |
3.72 |
4.09 |
3.78 |
4.02 |
4.33 |
4.33 |
3.98 |
3.61 |
3.96 |
4.04 |
3.86 |
3.94 |
4.02 |
3.81 |
4.16 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 3.55-3.65 и т.д.) и начертить гистограмму. Найти среднюю жирность молока по сгруппированной выборке, взяв в качестве вариант середины интервалов. Найти моду и медиану
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на моторное масло за 25-летний период с 1959 по 1983 гг.
Вариант 6
Имеются следующие данные о возрасте студентов (80 чел.) 1-го курса одного из факультетов:
17,19,18,17,17,18,19,24,21,28,20,17,18,18,18, 17,23,24,21,18,22,18,17,24,25,18,18,29,28,17, 18,18,18,19,20,20,18,18,22,21,27,20,18,18,32, 18,17,29,28,18,19,19,29,19,27,19,18,18,20,24, 27,18,19,18,18,20,18,18,25,26,23,18,18,19,17, 18,19,20.
Сгруппировать выборку, построить полигон часто. Найти моду, медиану и выборочную среднюю. Найти выборочную дисперсию и выборочное среднее квадратичное отклонение. Определить процент студентов, которые: а) только окончили школу; б) закончили школу не менее 10 лет назад.
В таблице приведены сведения о зарплате сорока восьми служащих одной фирмы.
1385 |
3200 |
1490 |
2100 |
2500 |
1500 |
1700 |
1250 |
2100 |
2800 |
2500 |
2400 |
1200 |
2000 |
1300 |
2300 |
1400 |
1250 |
2200 |
3000 |
1800 |
1600 |
3100 |
1900 |
2000 |
1500 |
1300 |
1200 |
1750 |
1500 |
2000 |
1750 |
1400 |
1600 |
1800 |
2200 |
2500 |
1300 |
1400 |
2500 |
1700 |
1850 |
2200 |
1400 |
1300 |
1850 |
1500 |
2200 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 1200 -1450 и т.д.) и начертить гистограмму. Найти среднюю зарплату. Найти моду и медиану. Какой процент сотрудников получает зарплату от 1550 до 2800 ден. ед.?
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на кухонное оборудование за 25-летний период с 1959 по 1983 гг.
Вариант 7
90 студентов получили следующее число оценок «хорошо»:
1,1,3,4,2,1,1,3,2,4,5,4,1,1,2,3,0,1,2,2,2,3,5,0, 5,2,2,0,1,1,1,1,4,2,1,1,3,3,0,5,2,2,1,1,2,2,2,3, 3,3,4,4,5,1,0,0,2,3,2,3,1,1,5,5,0,2,1,0,3,2,4,4, 0,0,2,1,2,1,0,1,0,3,0,5,0,5,0,4,4,5.
Сгруппировать выборку, построить полигон частот. Найти моду, медиану и выборочную среднюю. Найти выборочную дисперсию и выборочное среднее квадратичное отклонение. Определить процент студентов, которые: а) не получили оценки «хорошо»; б) получили не менее четырёх четвёрок.
Дана статистическая совокупность, характеризующая затраты (в копейках) на рубль продукции за 1990г. по 50 предприятиям г. Минска:
61.55 |
71.25 |
77.13 |
710.34 |
81.85 |
62.09 |
77.64 |
82.71 |
81.32 |
83.78 |
86.94 |
90.58 |
96.55 |
77.86 |
82.74 |
88.03 |
85.64 |
87.89 |
92.51 |
63.08 |
72.39 |
83.74 |
90.40 |
77.93 |
92.72 |
610.38 |
73.44 |
710.07 |
81.13 |
72.00 |
710.49 |
90.34 |
78.03 |
80.26 |
80.56 |
78.74 |
72.84 |
710.70 |
85.71 |
78.97 |
85.18 |
87.47 |
70.21 |
74.93 |
710.10 |
86.48 |
96.34 |
80.69 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 61.55 – 66.55 и т.д.) и начертить гистограмму. Найти средние затраты, взяв в качестве вариант середины интервалов. Какой процент в выборке составляют затраты от 75 до 85 (копеек на рубль)? Найти моду и медиану.
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на бензин за 25-летний период с 1959 по 1983 гг.
Вариант 8
Имеются данные 50 опытных участков о количестве внесённых удобрений (ц на 1 га):
4,4,2,7,9,10,5,2,9,3,3,4,6,10,9,9,9,5,6,6,5, 2,10,9,9,9,6,3,4,2,5,3,6,6,5,9,4,4,5,5,5,1,1,2,3,3,8,9,1,10
Сгруппировать выборку, построить полигон частот. Найти моду, медиану и выборочную среднюю. Найти выборочную дисперсию и выборочное среднее квадратичное отклонение. Определить процент участков, на которых удобрений внесено: а) менее 3 ц на 1 га; б) 5-7 ц на 1 га.
В таблице приведены результаты 50 пусков ракет в расстояниях (км) до точек падения:
40.26 |
40.37 |
40.33 |
40.28 |
40.29 |
40.40 |
40.44 |
40.38 |
40.35 |
40.35 |
40.41 |
40.30 |
40.33 |
40.33 |
40.32 |
40.37 |
40.44 |
40.44 |
40.35 |
40.40 |
40.31 |
40.37 |
40.34 |
40.37 |
40.35 |
40.35 |
40.30 |
40.36 |
40.33 |
40.34 |
40.39 |
40.42 |
40.39 |
40.30 |
40.36 |
40.31 |
40.38 |
40.34 |
40.39 |
40.35 |
40.41 |
40.35 |
40.28 |
40.29 |
40.27 |
40.31 |
40.37 |
40.31 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 40.26 – 40.30 и т.д.) и начертить гистограмму частот. Найти среднее расстояние, пройденное ракетой до падения, взяв в качестве вариант середины интервалов. Сколько ракет пролетели расстояние от 40,30 до 40,35 км (выразить в процентах)?
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на посуду за 25-летний период с 1959 по 1983 гг.
Вариант 9
Имеются данные 50 опытных участков об урожайности пшеницы (ц с га):
14,14,12,17,19,10,15,20,19,13,13,14,16,10,19,19,19,15,16,16,15,20,10,19,19,19,16,13,14, 20,15,13,16,16,15,19,14,14,15,15,15,11,11,12, 13,13,18,19,12,10.
Сгруппировать выборку, построить полигон частот. Найти моду, медиану и выборочную среднюю. Вычислить выборочную дисперсию и выборочное среднее квадратичное отклонение. Определить процент участков, урожайность которых: а)14 ц с га: б) более 17 ц с га.
Исследователь, изучающий выработку на одного рабочего-станочника механического цеха в отчётном году (в процентах к предыдущему году), получил следующие данные (в целых процентах) по 100 рабочим:
111,85,85,91,101,109,86,102,111,98,105,85,98,112,112,98,112,113,87,109,109,115,99,105,111,94,107,125,89,104,113,96,99,103,107,145,104, 105,88,103,97,115,109,89,108,107,97,106,107, 96,109,116,109,117,108,109,139,116,117,103, 127,119,118,125,105,116,117,106,101,113,107, 105,119,107,119,111,112,129,113,106,104,106,98,123,108,93,105,106,139,108,109,93,107,117,107,118,99,108,108,119,98,108,101,1010.
Построить интервальный вариационный ряд (первый интервал [80;90) ); построить гистограмму частот и найти выборочную среднюю, взяв в качестве вариант середины интервалов. Найти моду и медиану. Определить процент рабочих, у которых выработка: а) повысилась более чем на 10%; б) понизилась более чем на 10%.
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на питание за 25-летний период с 1959 по 1983 гг.
Вариант 10
Имеются данные 50 обследований о поставках сырья за месяц на предприятие (т):
15,17,18,15,12,20,18,19,16,14,15,18,19,21,20, 16,15,15,18,20,21,16,15,18,19,17,17,18,15,16, 20,16,19,20,21,19,19,18,19,15,17,15,17,18,21, 15,17,16,20,14,20.
Сгруппировать выборку, построить полигон частот. Найти моду, медиану и выборочную среднюю. Вычислить выборочную дисперсию и выборочное среднее квадратичное отклонение. Определить процент поставок: а) меньших 16 т; б) больших 18.
Дана статистическая совокупность, характеризующая длину нити в мотке пряжи (в метрах):
51.55 |
61.25 |
67.13 |
610.34 |
71.85 |
72.09 |
67.64 |
72.71 |
71.32 |
73.78 |
76.94 |
80.58 |
86.55 |
67.86 |
72.74 |
78.03 |
75.64 |
77.89 |
82.51 |
73.08 |
62.39 |
73.74 |
80.40 |
87.93 |
82.72 |
710.38 |
63.44 |
610.07 |
71.13 |
62.00 |
610.49 |
68.97 |
68.03 |
70.26 |
70.56 |
68.74 |
62.84 |
610.70 |
75.71 |
70.69 |
75.18 |
77.47 |
60.21 |
64.93 |
610.10 |
76.48 |
86.34 |
73.68 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 51.55 – 56.55 и т.д.) и начертить гистограмму. Найти среднюю длину нити в мотке, взяв в качестве вариант середины интервалов. Сколько мотков имеют длину нити от 70 до 80 метров (в процентах)? Найти моду и медиану
Исследовать зависимость располагаемого личного дохода (Х) населения США и текущих расходов (Y) на частное образование за 25-летний период с 1959 по 1983 гг.
Решение типового варианта
1. а) В ящике 5 красных и 4 белых шара. Наудачу берут 3 шара. Случайная величина Х – число белых шаров среди них. Составить закон распределения Х. Найти: 1) функцию распределения F(x) и построить её график; 2) моду, математическое ожидание MX и дисперсию DX.
Решение. Случайная величина Х распределена по гипергеометрическому закону. Она может принимать значения 0, 1, 2, 3 с вероятностями:
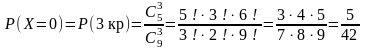 ,
,
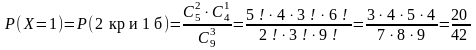 ,
,
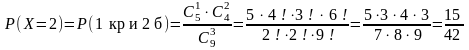 ,
,
 .
.
Запишем закон распределения случайной величины Х в виде таблицы:
-
X
0
1
2
3
Сумма
p
5/42
20/42
15/42
2/42
1
Мода
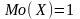 .
.
Функция распределения имеет вид:
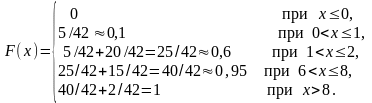
График этой функции изображён на рисунке 14.1.
Математическое ожидание:
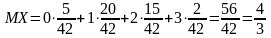 .
.
Дисперсия:
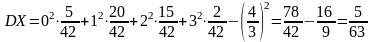 .
.
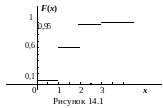
б) Тест состоит из трех вопросов. На каждый вопрос приведено 4 ответа, один из них правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание
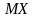 и дисперсию
и дисперсию
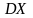 .
.
Решение.
Случайная
величина Х
распределена
по биномиальному закону с параметрами
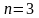 ,
,
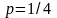 .
Х
может принимать значения 0, 1, 2, 3. Найдём
соответствующие вероятности по формуле
Бернулли
.
Х
может принимать значения 0, 1, 2, 3. Найдём
соответствующие вероятности по формуле
Бернулли
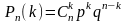 ,
учитывая, что
,
учитывая, что
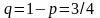 :
:
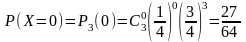 ,
,
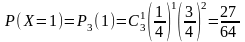 ,
,
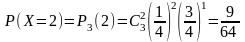 ,
,
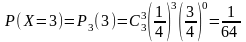 .
.
Запишем закон распределения случайной величины Х в виде таблицы:
-
X
0
1
2
3
Сумма
p
27/64
27/64
9/64
1/64
1
Математическое
ожидание и дисперсия для биномиального
закона находятся по формулам
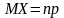 ,
,
 :
:
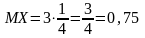 ,
, 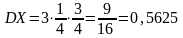 .
.
2. Построить дискретный вариационный ряд и начертить полигон для следующего распределения размеров 45 пар мужской обуви, проданных магазином за день:
-
39
41
40
42
41
40
42
44
40
41
42
39
41
37
43
41
38
43
40
39
41
40
42
40
41
42
38
40
43
42
41
43
39
42
42
39
43
42
41
40
41
38
44
41
41
Найти средний размер проданной обуви. Какой размер самый ходовой? Определить его процентное содержание. Найти выборочную дисперсию и выборочное среднее квадратичное отклонение. Найти моду и медиану.
Решение. Для построения вариационного ряда различные значения признака располагаем в порядке их возрастания и для каждого значения записываем его частоту (таблица 14.3).
Таблица 14.3.
|
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
Итого |
|
1 |
3 |
5 |
8 |
12 |
9 |
5 |
2 |
|
П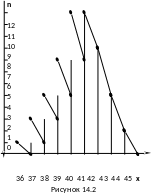 олигон
этого распределения изображен на рисунке
14.2.
олигон
этого распределения изображен на рисунке
14.2.
Средний размер обуви равен выборочной средней:
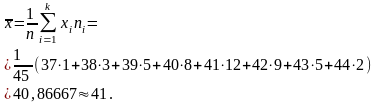
Самым
ходовым является также 41-ый размер, так
как он имеет самую большую частоту,
равную 12, поэтому
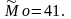 Медиана
Медиана
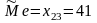 .
.
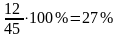 .
Это означает, что 27% проданной за день
обуви составляет обувь 41-го размера.
.
Это означает, что 27% проданной за день
обуви составляет обувь 41-го размера.
Найдём выборочную дисперсию по формуле
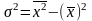 ,
где
,
где
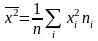 :
:
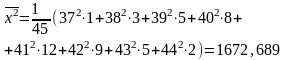
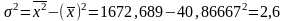 ,
, 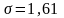 .
.
Наблюдения за толщиной (в мм) 50 слюдяных прокладок дали следующие результаты:
0,021 |
0,030 |
0,039 |
0,031 |
0,042 |
0,030 |
0,033 |
0,024 |
0,031 |
0,040 |
0,031 |
0,045 |
0,031 |
0,034 |
0,027 |
0,030 |
0,033 |
0,046 |
0,043 |
0,030 |
0,031 |
0,036 |
0,051 |
0,034 |
0,031 |
0,034 |
0,036 |
0,030 |
0,028 |
0,030 |
0,031 |
0,033 |
0,031 |
0,027 |
0,039 |
0,030 |
0,048 |
0,030 |
0,028 |
0,031 |
0,033 |
0,028 |
0,031 |
0,027 |
0,042 |
0,036 |
0,034 |
0,037 |
0,028 |
0,037 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 0,020 – 0,024, второй 0,024 – 0,028 и т.д.) и начертить гистограмму. Найти моду и медиану.
Решение. Для построения вариационного ряда построим таблицу, в первом столбце которой расположим в порядке возрастания интервалы, а во втором – соответствующие частоты (таблица 14.4).
Таблица 14.4.
-
Интервал
Частота
Накопленная частота
0,020 – 0,024
0,024 – 0,028
0,028 – 0,032
0,032 – 0,036
0,036 – 0,040
0,040 – 0,044
0,044 – 0,048
0,048 – 0,052
1
4
22
8
7
4
2
2
1
5
27
35
42
46
48
50
Найдём медиану по формуле:
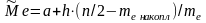 ,
,
где
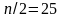 ,
,
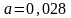 – начало медианного интервала,
– начало медианного интервала,
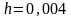 – длина интервала,
– длина интервала,
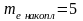 – частота, накопленная к началу медианного
интервала,
– частота, накопленная к началу медианного
интервала,
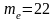 – частота медианного интервала.
– частота медианного интервала.
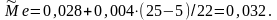
Моду найдём по формуле
 .
.
Модальный
интервал имеет самую большую частоту.
– начало модального интервала,
–
длина интервала,
 – частота интервала перед модальным,
– частота интервала перед модальным,
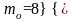 – частота интервала после модального,
– частота интервала после модального,
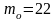 – частота модального интервала.
– частота модального интервала.
Гистограмма этого распределения изображена на рисунке 14.3.
Н
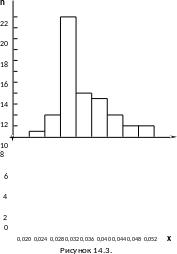 а
основании таблицы значений личного
располагаемого дохода (Х) населения
США и текущих расходов (Y)
на газ за 10-летний период с 1959 по 1983 гг.
(приложение С) найти:
а
основании таблицы значений личного
располагаемого дохода (Х) населения
США и текущих расходов (Y)
на газ за 10-летний период с 1959 по 1983 гг.
(приложение С) найти:
1) выборочные средние для Х и Y;
2) выборочную ковариацию между Х и Y;
3) выборочные дисперсии для Х и Y;
4) выборочный коэффициент линейной корреляции между Х и Y;
5) уравнение линейной регрессии Y на X;
6) коэффициент детерминации;
построить:
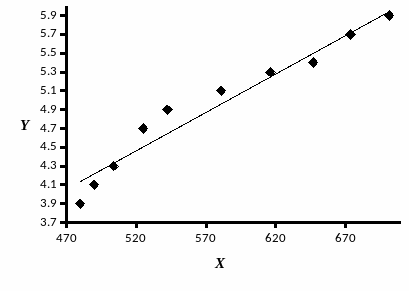
1) корреляционное поле;
2) график линейной регрессии Y на X (на одном графике с корреляционным полем).
Решение. Удобнее задачу решать на компьютере. Внесём данные в таблицу 14.5. и выполним действия, указанные в заголовке.
В клетках (12;2) и (12;3) таблицы вычислены выборочные средние
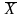 и
и
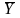 по формуле (12.6).
по формуле (12.6).Выборочные дисперсии
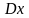 и
и
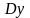 вычислены
в клетках (12.6) и (12;7) таблицы по формуле
(12.6).
вычислены
в клетках (12.6) и (12;7) таблицы по формуле
(12.6).
Выборочная ковариация
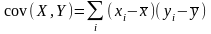 вычислена в клетке (12.8) таблицы.
Ковариация положительна, значит,
зависимость расходов на газ от дохода
прямая.
вычислена в клетке (12.8) таблицы.
Ковариация положительна, значит,
зависимость расходов на газ от дохода
прямая.Выборочный коэффициент линейной корреляции
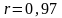 находится
в клетке (17;2) таблицы. Он вычислен по
формуле (13.5). Значение коэффициента
корреляции близко к единице. Это
означает, что связь между величинами
Х
и Y
прямая,
близкая к линейной.
находится
в клетке (17;2) таблицы. Он вычислен по
формуле (13.5). Значение коэффициента
корреляции близко к единице. Это
означает, что связь между величинами
Х
и Y
прямая,
близкая к линейной.Коэффициенты уравнения регрессии
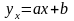 найдены в клетках (18;2) и (19;2) таблицы
соответственно по формулам (13.4) и (13.2).
Уравнение регрессии имеет вид:
найдены в клетках (18;2) и (19;2) таблицы
соответственно по формулам (13.4) и (13.2).
Уравнение регрессии имеет вид:
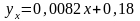 .
.
Коэффициент детерминации
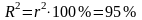 означает, что на 95% расходы на газ
обусловлены доходом, а на 15% зависят от
других факторов.
означает, что на 95% расходы на газ
обусловлены доходом, а на 15% зависят от
других факторов.
Т
123
аблица 14.5а.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||
|
Год |
X |
Y |
X-MX |
Y-MY |
(X-MX)2 |
(Y-MY)2 |
(X-MX)(Y-MY) |
||||
1 |
1959 |
479,70 |
3,90 |
-96,21 |
-1,03 |
9256,36 |
1,06 |
99,10 |
||||
2 |
1960 |
489,70 |
4,10 |
-86,21 |
-0,83 |
7432,16 |
0,69 |
71,55 |
||||
3 |
1961 |
503,80 |
4,30 |
-72,11 |
-0,63 |
5199,85 |
0,40 |
45,43 |
||||
4 |
1962 |
524,90 |
4,70 |
-51,01 |
-0,23 |
2602,02 |
0,05 |
11,73 |
||||
5 |
1963 |
542,30 |
4,90 |
-33,61 |
-0,03 |
1129,63 |
0,00 |
1,01 |
||||
6 |
1964 |
580,80 |
5,10 |
4,89 |
0,17 |
23,91 |
0,03 |
0,83 |
||||
7 |
1965 |
616,30 |
5,30 |
40,39 |
0,37 |
1631,35 |
0,14 |
14,94 |
||||
8 |
1966 |
646,80 |
5,40 |
70,89 |
0,47 |
5025,39 |
0,22 |
33,32 |
||||
9 |
1967 |
673,50 |
5,70 |
97,59 |
0,77 |
9523,81 |
0,59 |
75,14 |
||||
10 |
1968 |
701,30 |
5,90 |
125,39 |
0,97 |
15722,65 |
0,94 |
121,63 |
||||
11 |
10 |
5759,10 |
49,30 |
0,00 |
0,00 |
57547,15 |
4,12 |
474,69 |
||||
12 |
Среднее |
575,91 |
4,93 |
0,00 |
0,00 |
5754,71 |
0,41 |
47,47 |
||||
13 |
D |
5754,71 |
0,41 |
|
|
|
|
|
||||
14 |
cov(X,Y) |
47,47 |
|
|
Уравнение линейной регрессии Y на X |
|||||||
15 |
σв |
75,86 |
0,64195 |
|
Y = 0,0082x + 0,18 |
|||||||
16 |
rв |
0,97 |
|
|
X |
479,7 |
575,91 |
701,3 |
||||
17 |
a |
0,0082 |
|
|
Y |
4,14 |
4,93 |
5,96 |
||||
18 |
b |
0,18 |
|
|
|
|
|
|
||||
19 |
R2 |
0,95 |
|
|
|
|
|
|
||||
Построим корреляционное поле и линию регрессии на одном графике: