
Векторная алгебра. Скалярное произведение векторов.___________________________
Линейные операции над векторами
К линейным операциям над векторами относят сложение векторов, вычитание векторов, умножение вектора на число.
Вектора складываются по правилам треугольника и параллелограмма:
Правило треугольника |
Правило параллелограмма |
b
а
b
Для
того, чтобы вычислить сумму векторов
|
а
Для того, чтобы вычислить сумму векторов и по правилу параллелограмма нужно от начала вектора отложить вектор , достроить до параллелограмма и тогда вектор исходящий из общего начала векторов и и будет суммой этих векторов. |
Разность векторов представляется суммой с противоположным вектором.
В параллелограмме, построенном на двух векторах – одна диагональ является суммой этих векторов (исходящая из общего начала этих векторов), а другая – их разностью (начало которого совпадает с концом вектора вычитаемого, а конец которого совпадает с концом вектора уменьшаемого).
b


 b
b


а
![]()

Разложить вектор через векторы а и b:
M
|
|
B K C
A D
|
B C
|
Определить модули векторов:

 b
bа

Достроим до _________________ АВСD в котором

По теореме _______________ находим
b
а

Достроим до _________________ АВСD в котором
По теореме _______________ находим
 b
bа
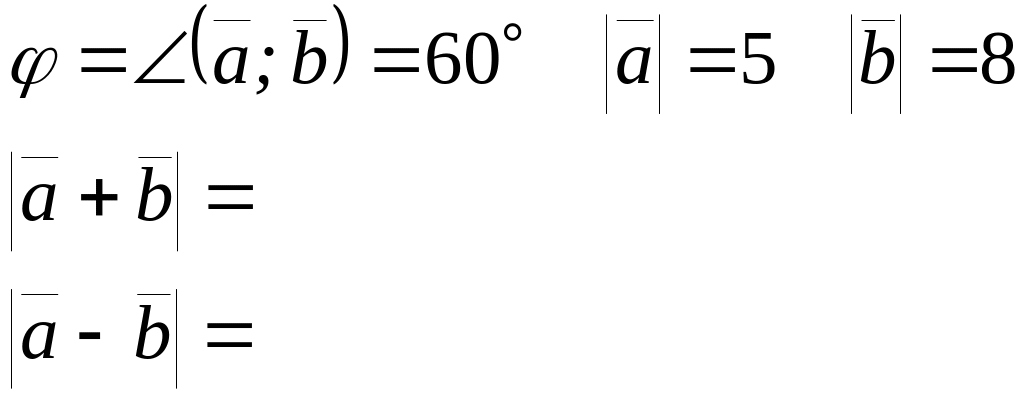
Достроим до _________________ АВСD в котором
По теореме _______________ находим
 b
bа

Достроим до _________________ АВСD в котором
По теореме _______________ находим
Определить модуль вектора:
b а
Достроим до _________________ АВСD в котором По теореме _______________ находим
|
а
Достроим до _________________ АВСD в котором По теореме _______________ находим
|
Пусть
векторы
={ax;
ay;
az}
и
={bx;
by;
bz}
заданы своими проекциями на оси координат
Ох,
Оу
и Oz
или, что то же
![]()
Из
определения векторы
и
называются
коллинеарными,
если
они лежат на одной прямой или на
параллельных прямых; записывают
![]() .
.
Векторы и коллинеарны, тогда и только тогда, когда их координаты пропорциональны, то есть







 b
b
b
b

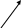
 B
B
 A
C
A
C


 B
B
 M
A1
M
A1


 A
B1
C
A
B1
C


 M
M





 A
A

 O D
O D F
E
F
E
 b
b