10. Расчет плиты на монтажные усилия

Расчетная схема панели при монтаже имеет вид:

q=6,64 кН/м

М онтажные петли располагаются на расстоянии 0,6 м = 60 см от торцов на нем.

Н

а = 0,6

агрузка от собственного веса панели:

q

а = 0,6

= t_red*p*b*k_d*Y_f=0,11*25*1,5*1,4*1,15 = 6,64 кН/м

Т

М=1,2 кН∙м

огда масса её составит: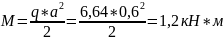

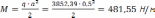
A_s = 12,6*8 = 101 мм²

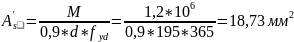
A_s < A^'_s имеющейся арматуры достаточно, следовательно, покрытие выдержит монтажную нагрузку.

Проверяем панель на монтажное усилие. Монтажные петли располагаются на расстоянии 0,6 м = 60 см от торцов на нем.

Расчёт монтажных петель

Определяем нагрузку от собственного веса панели:

p = q * ℓ_k = 6,64 * 6,45 = 42,83 кH

Усилие на одну петлю при условии передачи нагрузки от панели на три петли.

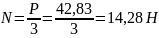
Определяем площадь поперечного сечения одной петли из стали класса S240

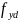( =218 Н/ мм^2-расчётное сопротивление стали класса S240 Ø5,5-40мм)

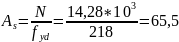мм²

Принимаем петли Ø 10 S240 A_s = 78,3 мм²

5. Расчет балки таврового сечения

1. Определяем нагрузку на 1м.п. ригеля:

От перекрытия

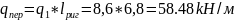
где

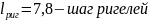
От собственного веса ригеля:

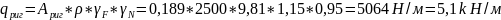
Полная нагрузка на ригель составит:

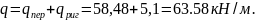
2. Ригель рассчитывается как однопролетная свободнолежащая на опорах балка, загруженная нагрузкой от перекрытия и собственного веса. Расчетное значение изгибающих моментов и поперечных сил определяем по формулам:

308,47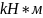

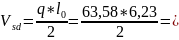198,05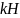

3. Расчет прочности ригеля по нормальным сечениям.

Рабочая высота сечения: d=h-c=450-50=400MM

Определяем значение α_m

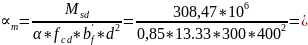0,57 >

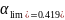
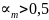=> сечение с двойным армированием.

Определяем площадь сжатой арматуры:

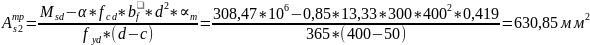
Принимаю 2стержня 22 с A_s2=760

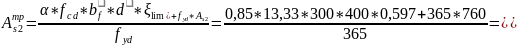2983,88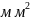

Рабочую арматуру принимаем: 4 стержня 32 S400, A_s1 = 3217мм².

К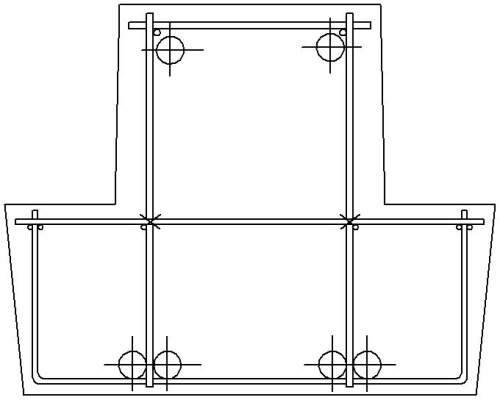 оэффициент армирования:

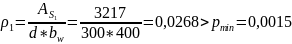
4. Расчёт прочности наклонных сечений на действие поперечной силы.

Необходимо проверить услови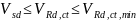е где 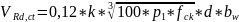, но не мение

где

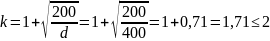
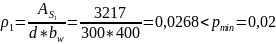
Поперечная сила, воспринимаемая железобетонным элементом без поперечной арматуры:

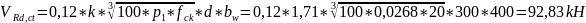
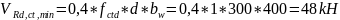
Проверяем условие - условие не соблюдается, требуется расчёт поперечной арматуры.

5. Для поперечного армирования принимаем арматуру 8 класса S400 A_sw1⁼50,3 мм.

Площадь сечения двух стержней: A_sw =2 50,3=100,6 мм².

По конструктивным требованиям принимаем шаг поперечной арматуры:

- на приопорных участках (при высоте h < 450 мм): h=450

S₁= 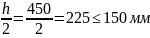, принимаем S₁= 150мм.

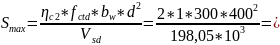484,73 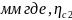=2,0

в середине пролёта (независимо от высоты):

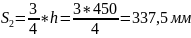< 500мм, принимаем S₂ = 300мм

Проверяем:

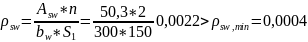
Определяем отношение:

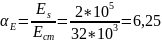
Определяем коэффициент:

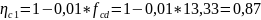
Определяем коэффициент:

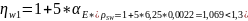
6. Проверяем несущую способность бетона по наклонной полосе между наклонными трещинами на действие главных сжимающих напряжений.

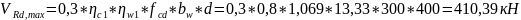
- условие соблюдается, следовательно, прочность бетона по наклонной полосе обеспечена.

7. Погонное усилие, воспринимаемое стержнями на единицу длины:

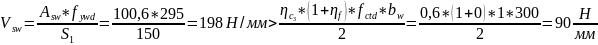
Определяем:

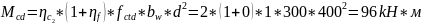
8. Горизонтальная проекция наклонного сечения:

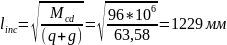
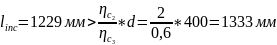
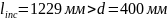
9. Длина проекции опасной наклонной трещины на продольную ось элемента:

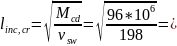696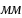

Проверяем:

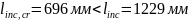
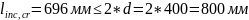
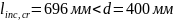
10. 0пределяем величину поперечной силы, воспринимаемой наклонным сечением:

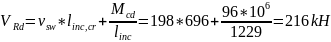
Окончательно принимаем для армирования поперечную арматуру 8 класса S240

A_sw1⁼100,6 мм².

11. Расчет полок ригеля.

На полки ригеля опираются панели перекрытия.

Расчет ведется на 1 м.п. ригеля (за ширину принимают b=1000мм).

Полка армируется сталью класса S240 f_yd=218H/мм².

Определяем опорную реакцию пустотной панели перекрытия шириной

В = 1,5 м на полку ригеля.

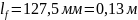
Рабочая высота сечения:

d=h-c=220-15=205мм

Определяем максимальный изгибающий момент:

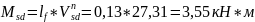
Определяем значение :

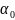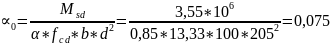
по таблице определяем :

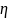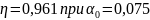
Определяем площадь растянутой арматуры на 1 м длины полки ригеля:

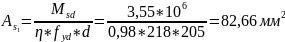
Принимаем шаг стержней 150 мм.

Количество стержней на 1 п.м. полки составит:

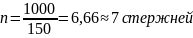
Принимаем 7 стержня 6 S240, A_s = 198 мм²