5. Законы Грассмана

Если на глаз действует смесь излучений, то реакции рецепторов на каждое из них складываются. Смешение окрашенных световых пучков даёт пучок нового цвета. Получение заданного цвета называется его синтезом. Законы синтеза цвета сформулировал Г. Грасман (1853 г.).

Первый закон Грасмана (трехмерности). Любой цвет однозначно выражается тремя, если они линейно независимы.

Линейная независимость заключается в том, что нельзя получить никакой из указанных трех цветов сложением двух остиальных. Закон утверждает возможность описания цвета с помощью цветовых уравнений.

Второй закон Грасмана (непрерывности). При непрерывном изменении излучения цвет изменяется также непрерывно.

Не существует такого цвета, к которому невозможно было бы подобрать бесконечно близкий.

Третий закон Грасмана (аддитивности). Цвет смеси излучений зависит только от их цветов, но не от спектрального состава.

Из этого закона следует факт, имеющий первостепенное значение для теории цвета, - аддитивность цветовых уравнений: если цвета нескольких уравнений описаны цветовыми уравнениями, то цвет выражается суммой этих уравнений.

6. Цветовое пространство Займемся теперь пространственным воображением. Из законов Грассмана (см. врезку) следует, что цвет можно выразить точкой в трехмерном пространстве. Трехмерное пространство для геометрического изображения цвета принято называть цветовым пространством. В нем каждому цвету будет соответствовать определенная точка, а каждой точке пространства - соответствующий цвет. В цветовой системе координат каждый цвет выражается через основные цвета этой системы, причем они должны быть линейно независимы (то есть ни один из них не должен получаться сложением двух других). Положение точки в пространстве, характеризующей тот или иной цвет, задается тремя координатами. Эту же точку можно рассматривать и как конец вектора, проведенного из начала координат (рис.2).

Рис.2.

Положение самого цветового вектора в цветовом пространстве и его длина не зависят от выбора основных, а определяются цветностью и яркостью цвета. Вектор цвета любого излучения можно представить цветовым уравнением. Для начала рассмотрим, что собой представляет цветовое пространство на примере системы RGB. Выразим некоторый цвет Ц в виде цветового уравнения. Цветовым уравнением называется уравнение, показывающее, в каких количествах нужно взять основные, чтобы в результате их смешения получить цвет, зрительно неотличимый от выражаемого уравнением. Пусть в нашем случае Ц - выражаемый уравнением цвет; R, G, B - цветовые координаты цвета Ц в системе основных RGB или, иными словами, количества основных, необходимые для получения цвета Ц; R, G, B - цвета излучений, принятые за основные. Тогда, в нашем случае, цветовое уравнение можно записать следующим образом:

Ц = RR + GG + BB

Сравнив это уравнение с уравнением свободного вектора в пространстве, рассматриваемого в векторной алгебре,

a = xi + yj + zk,

где i, j, k - тройка единичных векторов, легко убедиться, что они практически идентичны. (Мы выбрали колориметрическую систему RGB, но для рассмотрения сути дела могли бы с таким же успехом взять систему XYZ.) В нашем случае координаты цвета RGB будут определять проекции вектора цвета на координатные оси цветового пространства. Направление координатных осей можно выбирать любое, но удобнее принять цветовую координатную систему прямоугольной (рис.3).

Рис.3

На первый взгляд, рассматривать цвет в виде вектора в пространстве представляется бессмысленным. И в самом деле, вопрос о том, куда направлен вектор, например, желтого цвета, выглядит довольно странным. Тем не менее, в рассматриваемом цветовом пространстве RGB этот вектор имеет вполне определенное направление. Если он находится в плоскости GR и лежит ближе к оси G, то имеет зеленый оттенок, а если лежит ближе к оси R - красноватый. Таким образом, можно сказать, что направление вектора зависит от соотношения цветовых координат и характеризует цветность. Длина же самого вектора цвета зависит от суммы цветовых координат и выражает яркость. Вектор Ц соответствует цветам одинаковой цветности, но различной яркости. В цветовом пространстве в виде вектора можно представить и ахроматические цвета. Это возможно, когда координаты цвета (в нашем случае RGB) равны между собой. В этом случае яркость цвета увеличивается по оси ЧБ (рис. 4) от черного цвета через серый к белому. Ось ЧБ называется ахроматической осью. Соответственно, чем больше значения цветовых координат, тем больше яркость цвета. По мере удаления от ахроматической оси увеличивается насыщенность цвета.

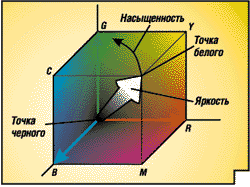
Рис.4

В современных специальных журналах часто используются такие понятия, как треугольник цветности, диаграмма цветности, локус, цветовой охват. Что это такое, как они образуются и для чего нужны, будет рассмотрено далее. А начнем рассмотрение этих понятий с принципа образования плоскости единичных цветов на примере системы RGB. Плоскость единичных цветов (Q) (рис. 5) проходит через отложенные на осях координат яркости единичных значений выбранных основных цветов. Единичным цветом в колориметрии называют цвет, сумма координат которого (или, по другому, модуль цвета m) равна 1. Поэтому можно считать, что плоскость Q, пересекающая оси координат в точках BR (R=1, G=0, B=0), BG (R=0, G=1, B=0) и BB (R=0, G=0, B=1), является единичным местом точек в пространстве RGB (рис. 5). Каждой точке плоскости единичных цветов (Q) соответствует след цветового вектора, пронизывающего плоскость в соответствующей точке с m=1. Следовательно, цветность любого излучения может быть представлена на плоскости единственной точкой. Можно себе представить и точку, соответствующую белому цвету (Б). Она образуется путем пересечения ахроматической оси с плоскостью Q (рис.5). Независимо от выбранной колориметрической системы плоскость единичных цветов, пересекаясь с координатными плоскостями, образует треугольник, называемый цветовым треугольником или треугольником цветности (рис. 5).

Рис.5.

В вершинах треугольника находятся точки основных цветов. Определение точек цветов, получаемых смешением любых трех основных, производится по правилу графического сложения. В колориметрии для описания цветности нет необходимости прибегать к пространственным представлениям. Достаточно использовать плоскость треугольника цветности (рис. 5). В нем положение точки любого цвета может быть задано только двумя координатами. Третью легко найти по двум другим, так как сумма координат цветности (или модуль) всегда равна 1. Поэтому любая пара координат цветности может служить координатами точки в прямоугольной системе координат на плоскости. В дальнейшем для рассуждений будет использована именно эта прямоугольная система. Итак, мы выяснили, что цвет графически можно выразить в виде вектора в пространстве или в виде точки, лежащей внутри треугольника цветности. Диаграмма цветности rg Попытаемся с помощью треугольника цветности rgb определить границы реально наблюдаемых цветов. Поскольку цветов более насыщенных, чем спектральные, не существует, то точки цветов, их выражающие, и будут определять эту границу. Выберем в прямоугольном треугольнике rgb одну из вершин, например b, за начало системы координат (b=0). Величины r=1 и g=1 отложим от начала координат соответственно по горизонтали и вертикали (рис. 6).

Рис. 6. Проецирование треугольника цветности на плоскость RG

Обозначим на треугольнике rgb значения координат цветности, соответствующие спектральным излучениям от 380 до 700 нм. Для этого воспользуемся кривыми сложения или удельными координатами rl, gl, bl, представляющими собой функции распределения по спектру цветовых координат монохроматических излучений мощностью в 1 Вт (рис. 7).

Рис 7

По их данным определим положение точек, соответствующих координатам цветности монохроматических излучений. Соединив эти точки, получим линию спектральных цветов. Кривая получается разомкнутой (рис. 8). Ее граничные точки соответствуют максимально насыщенным красному (l=700 нм) и фиолетовому (l=380 нм) цветам. Замкнув концы граничных точек прямой (на графике пунктирная линия), получим геометрическое место точек максимально насыщенных пурпурных цветов. Поскольку пурпурных цветов в спектре нет (пурпурные цвета представляют собой смесь красных и фиолетовых излучений), то и на пунктирной линии отсутствуют значения длин волн. Линия, являющаяся геометрическим местом точек цветности монохроматических излучений и замкнутая линией пурпурных, называется локусом (от лат. locus - место) (рис. 8). Внутри локуса находятся все реальные цвета. Вне локуса лежат воображаемые (или, как их еще часто называют, нереальные) цвета, более насыщенные, чем спектральные, выраженные в данной колориметрической системе.

Рис 8

Общими свойствами любого локуса, независимо от типа выбранной колориметрической системы, являются: А точка белого цвета имеет координаты (0,33; 0,33); Б насыщенность цветов возрастает от белой точки к локусу; В на прямой, соединяющей белую точку с локусом, лежат цвета одинакового цветового тона, но разной насыщенности. Нанеся на локус сетку прямоугольных координат, получают диаграмму цветности (рис.9). С помощью данной диаграммы можно определять цветовой тон и насыщенность того или иного цвета. Площадь, ограниченная локусом и замыкающей его линией пурпурных цветов, называется полем реальных цветов.

Рис 9

Как видно на рис. 9, цветности большинства излучений характеризуются отрицательной координатой r<0 , а у пурпурных g<0. Это затрудняет расчеты цвета по его спектральному составу. Кроме того, определение яркости цветов в системе RGB связано с расчетом всех трех координат цвета. Эти недостатки и послужили причиной создания системы XYZ. В продолжении темы мы рассмотрим эту систему наряду с равноконтрастными системами CIE, системами спецификации, а также разберемся с понятиями цветового охвата и цв--вого кон-ста DЕ.