Билет №1.
Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.
Вектор перемещения:
.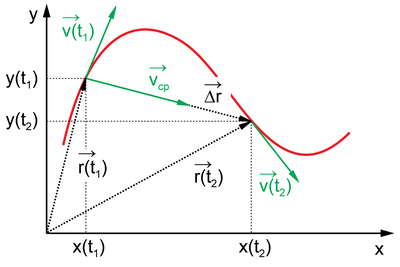
Вектор скорости (v) — это расстояние, которое тело проходит в определенном направлении за единицу времени.
Билет №2.
Координатный способ описания механического движения тела:
Координатный Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени. Движение одного и того же тела относительно разных тел оказывается различным.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда. Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Так можно поступать, например, при изучении движения планет вокруг Солнца. Если все части тела движутся одинаково, то такое движение называется поступательным.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x(t), y = y(t), z = z(t) (координатный способ), либо при помощи зависимости от времени радиус-вектора (векторный способ), проведенного из начала координат до данной точки
Определение скорости и ускорения точки при естественном способе задания движения
Естественные
оси (касательная, главная нормаль,
бинормаль) − это оси подвижной
прямоугольной системы координат с
началом в движущейся точке. Их положение
определяется траекторией движения.
Касательная (с единичным вектором ![]() )
направлена по касательной в положительном
направлении отсчета дуговой координаты
и находится как предельное положение
секущей, проходящей через данную точку
(рис.7.9). Через касательную проходит
соприкасающаяся плоскость (рис. 7.10),
которая находится как предельное
положение плоскости при
стремлении точки M1 к точке M. Нормальная
плоскость перпендикулярна касательной.
Линия пересечения нормальной и
соприкасающейся плоскостей − главная
нормаль. Единичный вектор главной
нормали
)
направлена по касательной в положительном
направлении отсчета дуговой координаты
и находится как предельное положение
секущей, проходящей через данную точку
(рис.7.9). Через касательную проходит
соприкасающаяся плоскость (рис. 7.10),
которая находится как предельное
положение плоскости при
стремлении точки M1 к точке M. Нормальная
плоскость перпендикулярна касательной.
Линия пересечения нормальной и
соприкасающейся плоскостей − главная
нормаль. Единичный вектор главной
нормали ![]() направлен
в сторону вогнутости траектории.
Бинормаль (с единичным вектором
направлен
в сторону вогнутости траектории.
Бинормаль (с единичным вектором ![]() )
направлена
перпендикулярно
касательной и главной нормали так, что
орты
)
направлена
перпендикулярно
касательной и главной нормали так, что
орты ![]() ,
, ![]() и
и ![]() образуют
правую тройку векторов. Координатные
плоскости введенной подвижной системы
координат
(соприкасающаяся, нормальная и спрямляющая) образуют естественный
трехгранник, который перемещается
вместе с движущейся точкой, как твердое
тело. Его движение в пространстве
определяется траекторией и законом
изменения дуговой координаты.
образуют
правую тройку векторов. Координатные
плоскости введенной подвижной системы
координат
(соприкасающаяся, нормальная и спрямляющая) образуют естественный
трехгранник, который перемещается
вместе с движущейся точкой, как твердое
тело. Его движение в пространстве
определяется траекторией и законом
изменения дуговой координаты.
Из
определения скорости точки 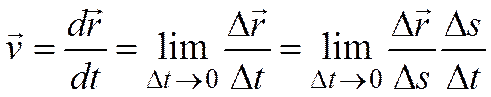 ,
,
где 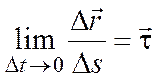 ,
, ![]() −
единичный вектор касательной.
Тогда
−
единичный вектор касательной.
Тогда
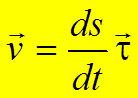 ,
, 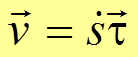 .
.
(симметрия, стремление к упрощению математических выкладок
и т.д.).
Билет №3
Динамика:
Точка, движение которой ничем не ограничено, называется свободной. Свободная точка под действием приложенных сил может двигаться в каком угодно направлении. P = ma.
Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела движутся прямолинейно и равномерно или покоятся
F=ma
1 Закон Ньютона: существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на неё внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.
Принцип относительности Галиллея:. все законы природы одинаковы во всех инерциальных системах отсчёта.
Закон сложения скоростей — абсолютная скорость материальной точки равна векторной сумме переносной и относительной скоростей.
Балет №4:
Масса: одна из важнейших физических величин. Первоначально она характеризовала «количество вещества»
Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей.
2 закон Ньютона: Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: F=ma
3 закон Ньютона: Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. F=-F
Билет №5
Система материальных точек- совокупность материальных точек или материальных тел, объединяемых общими законами взаимодействия(положение или движение каждой из точек зависит от положения и движения всех остальных)
Внутренние силы: Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок
Внешние силы: Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними..
И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
Билет №6
Механическая работа совершаемая силой постоянной F при перемещении тела на величину S равна скалярному произведению векторов силы и перемещения:
A=F*S=F*S*Cos alpha
Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
N=A/t
Билет №7
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек.
E=Mv^2/2
Чтобы у тела изменилась скорость, на тело должна подействовать сила. Но изменение скорости происходит при перемещении тела.
Можно установить прямую связь между силой, действующей на тело, его перемещением и изменением скорости тела на рассматриваемом участке траектории движения
Билет №8
Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и конечного положения тела, называются консервативными.
Консервативные силы: сила тяжести, электростатические силы, силы центрального стационарного поля. Неконсервативные силы: силы трения, силы вихревого электрического поля. Консервативная система – такая, внутренние силы которой только консервативные, внешние – консервативны и стационарны. Пример консервативных сил – гравитационные силы (рис. 5.3).
перемещения. Таким образом, из примера видно, что работа не зависит от формы пути, значит, силы консервативны, а поле этих сил потенциально.
Ek1 + Ep1 = Ek2 + Ep2. |
Закон сохранения механической энергии
Механическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может никуда исчезнуть. Для замкнутой системы физических тел, например, справедливо равенство Ek1 + Ep1 = Ek2 + Ep2, где Ek1, Ep1 — кинетическая и потенциальная энергии системы какого-либо взаимодействия,Ek2, Ep2 — соответствующие энергии после. Закон сохранения энергии — это интегральный закон. Это значит, что он складывается из действия дифференциальных законов и является свойством их совокупного действия.
Формулировка закона сохранения механической энергии.
Полная механическая энергия, т.е. сумма потенциальной и кинетической энергии тела, остается постоянной, если действуют только силы упругости и тяготения и отсутствуют силы трения.
1.20. Закон сохранения механической энергии
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Eр2 – Eр1). |
|
Билет №9
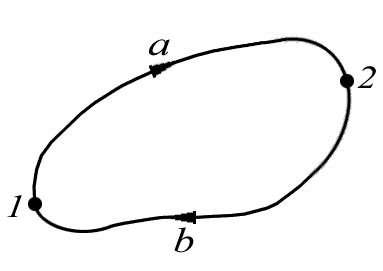
В потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле
|
Рис. 5.5. Работа в потенциальном поле сил |
потенциально,
то, по условию ![]() С
другой стороны, очевидно, что
С
другой стороны, очевидно, что ![]() Поэтому
Поэтому
![]()
Потенциальная энергия определяет силы упругости и силы тяжести, ее используют для определения электрических и магнитных сил, сил ядерного взаимодействия.
для
груза весом G,
поднятого на высоту h,
потенциальная энергия будет
равна:
![]() ;
(1)
для
груза, прикрепленного к
пружине:
;
(1)
для
груза, прикрепленного к
пружине:
![]() ,
(2)
где
,
(2)
где ![]() -
удлинение или сжатие пружины, k –
ее коэффициент жесткости; для двух
частиц с массами
-
удлинение или сжатие пружины, k –
ее коэффициент жесткости; для двух
частиц с массами ![]() и
и ![]() ,
притягивающихся по закону всемирного
тяготения:
,
притягивающихся по закону всемирного
тяготения:
![]() ,
(3)
где f –
гравитационная постоянная, r –
расстояние между частицами; аналогично
потенциальная энергия определяется и
для двух точечных электрических
зарядов
,
(3)
где f –
гравитационная постоянная, r –
расстояние между частицами; аналогично
потенциальная энергия определяется и
для двух точечных электрических
зарядов ![]() и
и ![]() .
.
Билет №10
Полная мех. Энергия-Сумма потенциальной и кинетической
полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы).
Учитывая, что при совершении работы A = Ek и, одновременно, A = - Ep, получим: Ek = - Ep или
(Ek + Ep)=0 - изменение суммы кинетической и потенциальной энергий (т.е. изменение полной механической энергии) системы равно нулю.
Значит, полная энергия системы остается постоянной:
E = Ep + Ek = const. В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется. (Или: полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы).