
4 Приклад роботи програмного комлексу
Розглянемо приклад роботи програмного комплексу на наступних вхідних даних:
ступінь першого багаточлену: 3;
коефіцієнти: 8 16 -2 4;
тобто перший багаточлен має наступний вигляд:
![]()
ступінь другого багаточлену: 2;
коефіцієнти: 4 -2 1;
тобто другий багаточлен має наступний вигляд:
![]()
На рисунку 4.1 показано результат роботи програми, запущеної з вказаними параметрами.
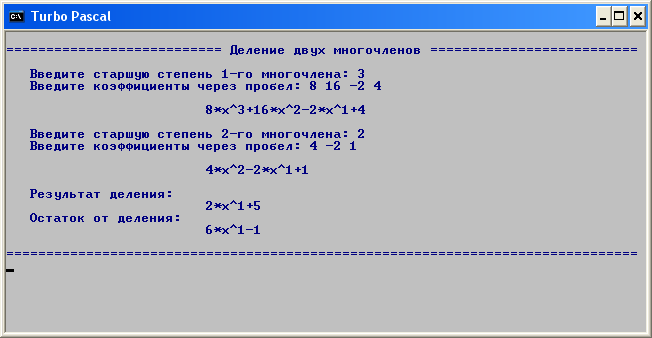
Рис. 4.1 – Результат роботи програми
Результатом роботи програми є вивід двох багаточленів: результату ділення та остатку від ділення. Результатом ділення також може бути багаточлен з нульовими коефіцієнтами, в випадку, якщо ділення неможливе на першому ж кроці.
Виконаємо перевірку отриманих результатів за допомогою середовища Mathcad. Умножимо отриманий результат ділення на дільник і додамо остаток, при цьому при правильних розрахунках повиннен вийти перший багаточлен. Скористаємося функцією Mathcad «expand» для розвернення отриманого виразу в поліном:
![]()
Оскільки отриманий вираз ідентичний першому багаточлену, отримано вірний результат.
Ділення неможливе за визначенням у випадку, якщо введено багаточлени такі, що ступінь другого більша за ступінь першого. В такому випадку програма видає відповідне повідомлення. Вікно з прикладом такого повідомлення показане на рис. 4.2.
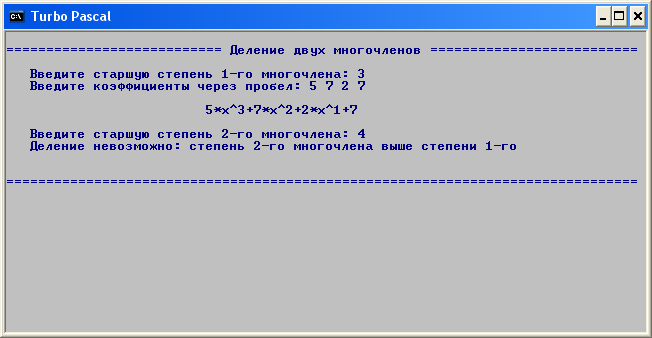
Рис. 4.2 – Вікно програми з повідомленням про неможливість ділення
ВИСНОВКИ
В процесі виконання курсової роботи розглянуті методи виконання цілочисельного ділення з остатком двох багаточленів довільних ступенів.
Розроблено алгоритм для програмної реалізації цілочисельного ділення двох багаточленів, заданих користувачем у вигляді коефіцієнтів при ступенях невідомих.
Створений програмний комплекс дозволяє для довільних двох багаточленів виконувати цілочисельне ділення з остатком, що значно полегшує аналогічні ручні розрахунки та може бути навчальним прикладом для людей, що вивчають правило ділення багаточленів «у стовбчик».
ПЕРЕЛІК ПОСИЛАНЬ
1 Шувалова Э. З., Агафонов Б. Г., Богатырёв Г. И. Повторим математику. М: Высшая школа, 1968г.
2 С. М. Олехник, М. К. Потапов, П.И. Пасиченко Уравнения и неравенства. Нестандартные методы решения: Справочник.
3 Выгодский М.Я. Справочник по элементарной математике. М: Наука, 1976 – 335 с.
RESUME
An object of work is a division two polynomials.
A purpose of work is development of programmatic complex for a division two polynomials, set an user.
A programmatic complex is developed by a programming of Turbo Pascal environment 7.0. He allows for the set coefficients two polynomials of different degrees to execute an operation them integer division from remain.
Work of programmatic complex is successfully tested for a few polynomials with different coefficients and senior degrees.
Work is made to order for the practical use in quality of rapid and comfortable mean for implementation of integer division from remain two polynomials of arbitrary degrees.
PROGRAMMATIC COMPLEX, POLYNOM, DIVISION, DIVIDEND, DIVIZOR, REMAIN, INTEGER DIVISION, DEGREE
ДОДАТОК А. ЛІСТИНГ ПРОГРАМИ
uses crt;
var
i:integer; {счетчик}
n1,n2,nn,ind:integer; {степени многочленов, вспомогательные переменные}
mnog1,mnog2,result:array[1..10] of integer; {массивы коэффициентов}
begin
textbackground(white); {цвет фона}
textcolor(blue); {цвет текста}
repeat
clrscr; {очистка экрана}
writeln;
writeln('=========================== Деление двух многочленов ==========================');
writeln;
write(' Введите старшую степень 1-го многочлена: ');
readln(n1);
write(' Введите коэффициенты через пробел: ');
for i:=1 to n1+1 do read(mnog1[i]);
writeln;
write(' ':25);
for i:=1 to n1+1 do {вывод многочлена в обычном виде, со степенями х}
begin
if (mnog1[i]>=0) and (i<>1) then write('+');
write(mnog1[i]);
if n1-i+1>0 then write('*x^',n1-i+1);
end;
writeln;
writeln;
write(' Введите старшую степень 2-го многочлена: ');
readln(n2);
if n2>n1 then
begin
writeln(' Деление невозможно: степень 2-го многочлена выше степени 1-го');
end
else
begin
write(' Введите коэффициенты через пробел: ');
for i:=1 to n1-n2+1 do mnog2[i]:=0;
for i:=i to n1+1 do read(mnog2[i]);
writeln;
write(' ':25);
for i:=n1-n2+1 to n1+1 do {вывод многочлена в обычном виде, со степенями х}
begin
if (mnog2[i]>=0) and (i<>n1-n2+1) then write('+');
write(mnog2[i]);
if n1+1-i>0 then write('*x^',n1+1-i);
end;
writeln;
writeln;
ind:=0;
nn:=n1;
repeat {цикл, реализующий деление многочленов "в столбик"}
result[n1-(nn-n2)+1]:=(mnog1[n1-nn+1] div mnog2[n1-n2+1]);
for i:=1 to n2+1 do
mnog1[n1-nn+i]:=mnog1[n1-nn+i]-result[n1-(nn-n2)+1]*mnog2[i+n1-n2];
if mnog1[n1-nn+1]<>0 then {если деление невозможно цикл заканчивается}
begin
ind:=nn-1;
break;
end;
nn:=nn-1;
if nn<n2 then break; {если деление завершено цикл заканчивается}
until false;
writeln(' Результат деления: ');
write(' ':25);
for i:=1 to n1-n2+1 do {вывод многочлена-результата деления}
begin
if (result[n2+i]>=0) and (i<>1) then write('+');
write(result[n2+i]);
if n1-n2-i+1>0 then write('*x^',n1-n2-i+1);
end;
writeln;
writeln(' Остаток от деления: ');
write(' ':25);
if ind=0 then {если деление было завершено удачно}
begin
for i:=1 to n1-nn+1 do {вывод многочлена-остатка деления}
begin
if (mnog1[n1-nn+i]>=0) and (i<>1) then write('+');
write(mnog1[n1-nn+i]);
if nn-i+1>0 then write('*x^',nn-i+1);
end;
end
else {иначе если на очередном шаге не удалось произвести деление}
begin
for i:=n1-ind to n1+1 do {вывод оставшейся части делимого многочлена}
begin
if (mnog1[i]>=0) and (i<>n1-ind) then write('+');
write(mnog1[i]);
if n1-i+1>0 then write('*x^',n1-i+1);
end;
end;
end;
writeln;
writeln;
writeln('===============================================================================');
until readkey=#27; {выход из программы при нажатии Esc}
end.
