1.4. Схема замещения для пленочной структуры Ta-Ta2o5-металл
График зависимости от частоты для комбинированной параллельно-последовательной схемы замещения показан на рис. 3, а сама схема изображена на рис. 4.
f
Рис.
3. Частотная характеристика
для комбинированной схемы замещения
R1
R2
C
Рис. 4. Параллельно-последовательная схема замещения
График, представленный на рис. 4, можно объяснить следующим образом. С ростом частоты приложенного напряжения увеличивается проводимость конденсатора и напряжение перераспределяется на R2. Для адекватного отражения физических процессов в диэлектриках необходимо, чтобы соблюдалось условие R1>>R2. Поэтому диэлектрические потери определяются контуром C-R2, т.е линейно увеличивается с ростом частоты. В области низких частот вследствие высокого сопротивления C и R1 напряжение почти целиком падает в параллельном контуре и, следовательно, растет с уменьшением частоты.
Частотная характеристика, показанная на рис. 3, характерна для пленочных структур Ta-Ta2O5-металл. Физическое объяснение этого факта заключается в следующем. Резистор R1 в комбинированной схеме замещения отражает слабые места в оксидной пленке, сквозь которые течет слабый электрический ток, так называемый ток утечки. Резистор R2 является электрическим аналогом высокого сопротивления пленки тантала, на которой сформирован слой диэлектрика.
1.5. Расчетные формулы
Для комбинированной схемы замещения (рис.4) формула для тангенса угла диэлектрических потерь имеет вид:
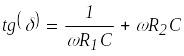(3)
При малых частотах из (3) получаем:
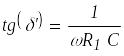(4)
Если
построить график зависимости
от 1/
,
то получится прямая с углом наклона
,
причем
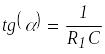(5)
Аналогично при устремлении к бесконечности
(6)
Прямая
на графике зависимости
от
имеет угол наклона
такой, что
(7)
Если
продифференцировать (3) по
,
то для угловой частоты
,
соответствующей минимуму
на рис. 3, можно получить выражение
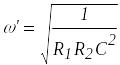(8)
Измерив зависимость от , построив графики от 1/ и от и использовав формулы (5) и (7), можно рассчитать R1•C и
R2 •C.
Формулу (8) можно использовать для проверки результатов. Однако, для того, чтобы вычислить по отдельности R1, R2 и C, необходимо также измерить зависимость емкости от частоты.