
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Филиал государственного образовательного учреждения высшего
профессионального образования «Уфимский государственный нефтяной
технический университет» в г. Салавате
КУРС ЛЕКЦИИ ПО РАЗДЕЛУ МАТЕМАТИКИ
«КОМБИНАТОРИКА И ЭЛЕМЕНТЫ ЛОГИКИ»
Составитель: Хазиев Ф.М., доцент
Салават 2008
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, заведующему учебной частью школы – составить расписание уроков и т.д.
Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.
Комбинаторика возникла в XVI веке. В жизни привилегированных слоёв тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Одним из первых занялся подсчётом числа различных комбинаций при игре в кости итальянский математик Тарталья. Дальнейшее развитие комбинаторики связано с именами Якова Бернулли, Лейбница и Эйлера. За последние годы комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний; для составления планов производства и реализации продукции.
Пусть имеется n предметов, отмеченных числами 1, 2, … , n. Из этих предметов выбираем один, записываем число, на нём изображённое, а сам предмет либо возвращаем назад ( в этом случае говорят о выборе с возвращением ), либо он убирается и больше не может быть выбран ( в этом случае говорят о выборе без возвращения ). Повторяем эту процедуру k раз.
Запись, полученная в результате всех действий, называется выборкой из n элементов по k.
Запись, полученная по схеме выбора с возвращением, называется выборкой с повторениями, а запись, полученная по схеме выбора без возвращений, называется выборкой без повторений.
Общие правила комбинаторики
Комбинаторные задачи бывают самых разных видов. Но большинство задач решается с помощью двух основных правил – правила суммы и правила произведения.
Правило суммы: если некоторый
объект А можно выбрать
 способами, а другой объект В можно
выбрать
способами, а другой объект В можно
выбрать
 способами, то выбор «либо А, либо В»
можно осуществить
способами, то выбор «либо А, либо В»
можно осуществить
 способами.
способами.
При использовании правила суммы в
последней формулировке надо следить,
чтобы ни один из способов выбора объекта
А не совпадал с каким-нибудь способом
выбора объекта В (или, как мы говорим,
чтобы ни одна комбинация не попала сразу
в два класса). Если такие совпадения
есть, правило суммы утрачивает силу, и
мы получим лишь
 способов выбора, где
способов выбора, где
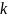 - число совпадений.
- число совпадений.
Правило произведения: если объект
А можно выбрать
способами и если после каждого такого
выбора объект В можно выбрать
способами, то выбор пары (А,В) в указанном
порядке можно осуществить
 способами.
способами.
Задача 1. В магазине лежат 6 экземпляров романа И.С.Тургенева «Рудин», 3 экземпляра его же романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, есть 5 томов, содержащих романы «Рудин» и «Дворянское гнездо» и 7 томов, содержащих романы «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?

Соединения в комбинаторике
Различные группы, составленные из каких-либо предметов и отличающиеся одна от другой или порядком этих предметов, или самими предметами, называются соединениями.
Предметы, из которых составляются
соединения, называются элементами.
Элементы обозначаются буквами
 .
.
Соединения могут быть трёх видов: размещения, перестановки, сочетания без повторений и с повторениями.
Рассмотрим каждый из видов в отдельности.
Размещения без повторений
Определение. Размещениями из
элементов по
называются такие соединения, каждое из
которых содержит
элементов, взятых из данных
элементов, и которые отличаются одно
от другого или элементами, или порядком
элементов и обозначается
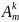 .
.
Другими словами, если две выборки, отличающиеся только порядком записи символов, считают различными, то говорят о размещении из m элементов по k.
Пусть дано
элементов:
 .
Сначала составим из них все размещения
по 1.
.
Сначала составим из них все размещения
по 1.

Их, очевидно, будет
.
Значит,
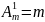 .
.
Теперь составим все размещения по 2. Для
этого к каждому из ранее составленных
размещений по 1 приставим последовательно
все оставшиеся
 элементов по 1. Так, к элементу
элементов по 1. Так, к элементу
 приставим последовательно оставшиеся
элементы:
приставим последовательно оставшиеся
элементы:
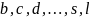 ;
к элементу
;
к элементу
 приставим последовательно оставшиеся
элементы:
приставим последовательно оставшиеся
элементы:
 и т.д. Получим следующие размещения по
2:
и т.д. Получим следующие размещения по
2:
m строк |

Так как всех элементов
,
то из каждого размещения по одному
элементу мы получим
размещений по 2, а всего их будет
 .
Значит,
.
Значит,
 .
.
Чтобы составить размещения по 3, берём
каждое из составленных сейчас размещений
по 2 и приставим к нему последовательно
по одному все
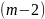 оставшихся элементов. Тогда получим
следующие размещения по 3:
оставшихся элементов. Тогда получим
следующие размещения по 3:
m(m-1) строк |

Так как число всех размещений по 2 равно
m(m-1) и из
каждого получается m-2
размещения по 3, то всех таких размещений
окажется: m(m-1)(m-2).
Таким образом
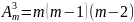 .
Подобно этому получим:
.
Подобно этому получим:

 ,
и вообще:
,
и вообще:

Числитель
и знаменатель умножим на произведение
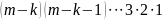

 .
.

Пример 2. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского, на любой другой из этих пяти языков?





