
7.6 Особенности кодирования в реальных каналах
Кодек
помехоустойчивого кода является
составной частью дискретного канала
связи (ДКС). Диаграмма состояний и
переходов для двоичного дискретного
канала связи показана на рис. 7.14, где
 –
элементы алфавита источника;
–
элементы алфавита источника;
 –
элементы алфавита на выходе канала;
–
элементы алфавита на выходе канала;
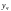 –
символ стирания;
–
символ стирания;
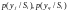 –
переходные вероятности, где
–
переходные вероятности, где
 .
В канале без стираний состояния
.
В канале без стираний состояния
 и соответствующие переходы отсутствуют.
и соответствующие переходы отсутствуют.
 Математическая
модель дискретного канала требует
описания следующих параметров канала:
алфавитов входных и выходных сообщений;
скорости передачи элементов алфавита;
переходных вероятностей
Математическая
модель дискретного канала требует
описания следующих параметров канала:
алфавитов входных и выходных сообщений;
скорости передачи элементов алфавита;
переходных вероятностей
 .
.
Характеристики непрерывного канала (в том числе характер действия помех в линии связи) проявляются в свойствах переходных вероятностей ДКС. В результате этого ДКС могут быть:
1)
симметричными,
когда переходные вероятности
 одинаковы
для всех
одинаковы
для всех
 и,
соответственно, несимметричными
в противном случае;
и,
соответственно, несимметричными
в противном случае;
2)
без
памяти,
когда переходные вероятности
не
зависят от того, какие символа и с каким
качеством передавались до данного
символа
 ,
и с
памятью
в
противном случае;
,
и с
памятью
в
противном случае;
3) без стирания, когда алфавиты на входе канала и выходе демодулятора совпадают, в канале со стиранием алфавит на выходе демодулятора имеет дополнительный символ стирания , формируемый тогда, когда демодулятор не может с заданной надежностью опознать переданный символ.
Математической моделью ДКС без памяти является биномиальный канал, ошибки в этих каналах независимы и определяются вероятностью ошибки . Такой канал является отображением в дискретном пространстве стационарного непрерывного канала с гауссовским шумом. В практике связи это во многих случаях кабельные и волоконно-оптические каналы электросвязи, магистральные каналы РРЛ с высокой энергетикой, спутниковые и космические каналы в отсутствии импульсных помех.
В каналах с независимыми ошибками (биномиальный канал) как для обнаружения, так и для исправления ошибок используются либо циклические коды БЧХ, либо свёрточные коды.
Вероятность ошибки в кодовом слове на входе декодера равна вероятности ошибки хотя бы в одном из символов этого слова:
 , (7.27)
, (7.27)
а
вероятность правильного приёма
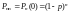 .
.
Тогда вероятность обнаружения ошибки помехоустойчивым кодом с кодовым расстоянием будет равна:
 , (7.28)
, (7.28)
а вероятность исправления ошибки, соответственно, равна:
 . (7.29)
. (7.29)
В режиме исправления ошибок вероятность ошибки декодирования кодового слова на выходе декодера равна:
 ,
(7.30)
,
(7.30)
или, с учетом возможно больших значений ,
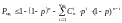 =
= . (7.31)
. (7.31)
Знак неравенства относится к тем случаям, когда декодер обнаруживает и исправляет ошибки не только в пределах гарантированной кратности, определяемой кодовым расстоянием (7.4, 7.5).
Оценка
вероятности ошибки декодирования на
один информационный символ, когда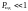 ,
равна:
,
равна:
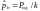 .
.
Исправление ошибок в тех случаях, когда декодер только обнаруживает ошибки, производится в системах передачи с переспросом. Такие системы передачи должны иметь обратный канал и относятся к системам с обратной связью.
