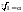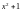7.2 Групповые коды Арифметика в полях Галуа

В теории помехоустойчивого кодирования широко используются теория множеств, высшая алгебра, векторные пространства и алгебра логики. Одно из важнейших достижений алгебры – это создание алгебраических систем, использование которых позволяет осуществить практическую реализацию кодов. Алгебраические системы состоят из множеств и операций над элементами этих множеств. В теории кодирования из алгебраических систем, в основном, используются группы и поля.

Группой называется множество элементов с определенной для каждой пары элементов операцией (обозначим эту операцию *), обладающее следующими четырьмя свойствами:

1) Замкнутость:

2) Ассоциативность:

3) Существование единицы: существует такой единичный (нейтральный) элемент , что , для любого 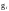-того элемента группы ;

4) Существование обратного элемента:

Если группа содержит конечное число элементов , то она называется конечной группой, а число элементов в ней называется порядком группы.

Если конечная группа обладает свойством коммутативности , то это коммутативная (или абелева) группа.

Если для группы используется операция сложения, то группа называется аддитивной, а единичный элемент – нулем, то есть , обратный элемент , а .

Если для группы используется операция умножения, то группа называется мультипликативной, а единичный элемент - единицей, т.е. ; – обратный элемент, а

В группе может быть только один единичный элемент.

Минимальная аддитивная группа, имеет порядок 2 {0, 1}, а минимальная мультипликативная группа – порядок 1 {1}.

Порядком элемента аддитивной группы называется число , для которого справедливо равенство , где – это элемент группы. Причем всегда . Если , то порядок элемента совпадает с порядком группы. Элемент в этом случае называется примитивным элементом. Примитивный элемент группы позволяет найти все элементы группы.

Порядком элемента мультипликативной группы называется наименьшее удовлетворяющее условию: , то – это порядок элемента мультипликативной группы. Порядок единичного элемента всегда равен единице: 1¹=1.

Например, имеется мультипликативная группа относительно операции умножения по :

Тогда: 11=1¹ =1 (порядок элемента 1 равен 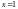), единичный элемент; 2222=2⁴ =1 (порядок элемента 2 равен x=4, а по ), т.е. 2 примитивный элемент; 3333=3⁴ =1 (порядок элемента 3 равен 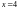, а ), т.е. 3 примитивный элемент; 44=4²=1 (порядок элемента 4 равен ), т.е. 4 – это непримитивный элемент.

Подгруппа – это подмножество множества ( ), такое, что замкнуто относительно операции множества .

Например.

Аддитивная группа . Аддитивные подгруппы: =0 – для любой аддитивной группы; ={0, 2, 4}.

Мультипликативная группа Мультипликативные подгруппы: ={1} ; ={1, 4}.

Циклическая подгруппа (группа) состоит из степеней одного элемента , если – это порядок подгруппы. Циклическими группами являются все мультипликативные и аддитивные группы относительно умножения или сложениия по модулю простого числа( …и т.д.).

Полем называется множество , которое является аддитивной абелевой группой, ненулевые элементы образуют мультипликативную группу, для всех элементов множества выполняется закон дистрибутивности. Характеристикой поля является примитивный элемент аддитивной группы, образующей поле; примитивные элементы мультипликативной группы являются примитивными элементами поля.

В теории помехоустойчивого кодирования используются поля с конечным числом элементов – поля Галуа . Обозначение: = , где – характеристика поля (должно быть простым числом), – порядок расширения поля (целое число). При этом –простое поле Галуа; – расширение поля Галуа порядка ,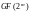 – расширение двоичного поля Галуа порядка . Простое двоичное поле Галуа имеет два элемента{0, 1}, расширение поля имеет элементов. В поле 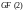и его расширениях сложение и умножение выполняются по ; если элемент поля, то (обратным элементом является сам элемент).

Линейным векторным пространством над полем называется множество объектов (векторов), для которых определены две операции: векторное умножение и умножения вектора на элемент поля.

Например, если -элемент поля и - вектор над полем , тогда 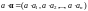является вектором этого же пространства.

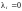Множество векторов являются линейно независимыми и называются базисом векторного пространства, если , только когда все , где некоторые скаляры. Векторное пространство, содержащее нулевой вектор является линейно зависимым.

Базис векторного пространства порождает - мерное векторное пространство, объекты которого могут быть получены линейной комбинацией базисных векторов в виде . Причём в - мерном пространстве любое множество, содержащее более векторов, является линейно зависимым. Подпространство линейного векторного пространства имеет размерность меньше и должно быть замкнуто относительно операции сложения.

Умножение вектора на матрицу , где –– вектор над полем, а матрица

Если имеет один столбец, то произведение скалярно.

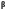Произведение векторов и равно , где – транспонированный вектор. Для ортогональных векторов .

Если вектор – элемент линейного векторного пространства (элемент поля), то его можно записать в виде полинома (многочлена) .

Если имеется 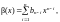то определена операция сложения полиномов .

Умножение полиномов 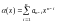и производится по правилам умножения в двоичном поле

(7.12)

где , т.е. -й скаляр полинома является, по сути, сверткой скаляров полиномов-сомножителей.

Умножение по модулю полинома p(x):

, (7.13)

где – остаток от деления произведения на .

Если нельзя представить в виде сомножителей, то называется неприводимым (примитивным) полиномом. Неприводимый полином в дальнейшем будем обозначать .

Деление полиномов по модулю полинома :

, (7.14)

где 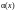– остаток от деления на полином .

Множество полиномов , где и , образует поле над ; – производящий полином.

Пусть производящий полином поля 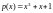. Тогда порядок расширения поля определяется степенью производящего полинома и, следовательно, . Количество элементов поля 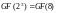с нулем равно 8 (аддитивная группа), без нуля (мультипликативная группа).

Обозначим примитивный элемент поля , который также является корнем производящего полинома. Примитивный элемент (множество его степеней) порождает все элементы поля и является первообразным корнем из единицы, т.к. (таблица 7.3).

Т а б л и ц а 7.3 – Элементы поля Галуа

Степени	Значения	Полином	Двоичная запись
[ ] и т.д.	, т.е.		001 010 100 011 110 111 101 001

Запись элементов поля в виде полиномов удобно использовать для сложения элементов поля, а в виде степеней 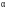- при умножении элементов поля. Например, сложение элементов поля: или 011+110 = 101 = ;

умножение элементов поля: .

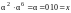Заметим также, если – это корень неприводимого полинома , то – также являются корнями . Таким образом, зная один корень, можно определить все корни. Поэтому неприводимые полиномы называют еще минимальными функциями над полем .

Можно показать, что все элементы поля и только они являются корнями полинома для . Если – элемент поля , то, подставляя этот элемент поля в , получаем , так как примитивный элемент поля в степени всегда равен 1. Следовательно, если корни минимальных функций являются корнями , то Это свойство широко используется при формировании производящих полиномов циклических кодов.