7. Теория помехоустойчивого кодирования

7.1 Основные понятия и определения

Помехоустойчивое кодирование - это преобразование дискретного множества сообщений в другое, более мощное (избыточное) множество, которое позволяет обнаруживать и исправлять ошибки, возникающие в канале связи в процессе передачи кодовых символов. Выбор этого множества (помехоустойчивого кода) зависит от свойств канала (статистики ошибок в дискретном канале). Поэтому помехоустойчивое кодирование иногда называют канальным кодированием.

Помехоустойчивые (или корректирующие) коды имеют различные приложения: для защиты от ошибок в вычислительных устройствах и сетях, системах хранения данных, спутниковых и навигационных системах, в системах сотовой связи, при цифровой передаче аудио и видеосигналов. В специальных приложениях они используются для защиты информации от преднамеренно организованных помех.

Классификация и основные параметры помехоустойчивых кодов

В настоящее время известно большое количество кодов, отличающихся по помехоустойчивости и способам построения. Применение некоторых из них ограничивается сложностью технической реализации кодеков (объединенное название кодера и декодера). Рассмотрим классификацию кодов, наиболее часто используемых на практике.

Двоичные и недвоичные коды отличаются друг от друга основанием кода ; если , то код является недвоичным (соответственно, троичным, четверичным и т.д.).

У линейных кодов избыточные (проверочные) символы образуются в результате линейных операций над информационными символами. Большинство используемых на практике помехоустойчивых кодов являются линейными (циклические, сверточные и др.), так как они относительно просто кодируются и декодируются. Нелинейные коды (с постоянным весом, инверсные и некоторые другие) используются, в основном, в специальных приложениях, так как часто имеют лучшие параметры.

Систематические коды – такие коды, у которых информационные символы в процессе кодирования не изменяются, а кодер вычисляет и добавляет к ним проверочные символы.

У блочных кодов, в отличие от непрерывных, последовательность кодовых символов на выходе кодера делится на кодовые слова (блоки), а в декодере каждое слово из символов декодируется отдельно.

Каскадные коды образуются параллельным или последовательным соединением нескольких помехоустойчивых кодов.

Циклические коды относятся к линейным блочным кодам и широко используются в практике передачи данных как в системах связи, так и в специальных приложениях. Среди циклических кодов в каналах с независимыми ошибками наибольшее распространение получили коды Боуза–Чоудхури–Хоквингема (БЧХ).

Свёрточные коды относятся к линейным непрерывным кодам и получили широкое распространение в последние годы в космических и радиорелейных системах передачи.

Известны также ряд кодов, имеющих лучшие параметры или обеспечивающих лучшие характеристики декодирования в каналах с определённой статистикой ошибок.

Кодер помехоустойчивого кода преобразует поток данных, поступающих на его вход от источника сообщений, в новый поток кодовых элементов (символов) путем разбиения на кодовые слова (кодовые комбинации) и добавления избыточности, необходимой для борьбы с помехами в канале связи. В общем случае элементный равномерный код с основанием имеет возможных кодовых слов. Благодаря избыточности для передачи сообщений используется только часть кодовых слов (из множества ), которые называют разрешенными, остальные кодовые слова 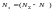не используются и называются запрещенными. Если в результате искажений в канале связи переданное кодовое слово превращается в одно из запрещенных слов , то декодер приёмника обнаруживает ошибку, так как такое слово не могло быть передано. Ошибка не обнаруживается только в том случае, когда передаваемое кодовое слово превращается в другое разрешенное, например, , которое также могло быть передано.

По сравнению с обнаружением исправление ошибок представляет собой более сложную операцию, поскольку в этом случае помимо обнаружения наличия ошибки в принятом кодовом слове декодер должен определить местоположение искаженного кодового символа и значение ошибки (для недвоичных кодов). Чтобы рассматриваемый код исправлял ошибки, необходимо часть или все множество запрещенных кодовых слов разбить на непересекающихся подмножеств по количеству разрешенных кодовых слов. Каждое из этих подмножеств в декодере приемника приписывается одному из разрешенных кодовых слов. Если принятое кодовое слово принадлежит подмножеству , то переданным считается разрешенное кодовое слово . Ошибка не может быть исправлена, если переданное кодовое слово в результате искажений превращается в кодовое слово любого другого подмножества .

Основные параметры и характеристики помехоустойчивых кодов.

1. Избыточность кода

(7.1)

где и – количество информационных и проверочных символов в символьном кодовом слове.

2.Скорость кода . (7.2)

3. Расстояние Хэмминга между двумя кодовыми словами

где – координаты разрешённых кодовых слов 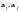в -мерном неевклидовом пространстве.

Если код является двоичным, то расстояние между парой кодовых слов равно количеству символов, в которых они отличаются. Например, если то

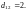
4. Спектр весов кода – это распределение весов ненулевых кодовых слов, где – вес -го кодового слова, который равен числу ненулевых символов этого слова.

5. Минимальное расстояние Хэмминга называется кодовым расстоянием данного кода:

(7.3)

6.Обнаруживающая и исправляющая способности корректирующих кодов тесно связаны с расстояниями между разрешенными кодовыми словами. Так как кратность ошибки является расстоянием Хэмминга между переданным словом и принятым, то для гарантированного обнаружения ошибок кратности не менее 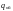требуется кодовое расстояние:

(7.4)

Для гарантированного исправления ошибок кратности не менее , требуется кодовое расстояние:

(7.5)

Это означает, что для исправления ошибок искаженное кодовое слово в -мерном пространстве должно располагаться ближе всего к соответствующему правильному слову.

В случае исправления ошибок и 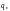стираний необходимое кодовое расстояние определяется выражением:

(7.6)

Очевидно, что наилучшим как для исправления, так и для обнаружения ошибок будет код с наибольшим кодовым расстоянием. Для нахождения кодов с хорошими корректирующими свойствами используются границы. Так, например, известны границы Хэмминга и Плоткина, которые позволяют определить необходимое число проверочных символов в кодовом слове.

Граница Хэмминга имеет вид:

Граница Плоткина имеет вид: (7.7)

Граница Хемминга утверждает, что не существует кодов с

, гарантированно исправляющих ошибки кратности _, а граница Плоткина утверждает, что могут быть построены (существуют) коды с . Граница Хэмминга обеспечивает избыточность кода, близкую к минимальной, при больших значениях , а граница Плоткина - при малых.

Оптимальными обычно считаются такие 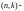коды, которые обеспечивают в заданном канале меньшую вероятность ошибки декодирования при одинаковой скорости кода и одинаковой вычислительной сложности декодирования.