11.3 Момент трения подшипников скольжения

11.3.1 Расчет радиального момента трения.

При определении момента трения М_тр в подшипнике скольжения под действием радиальной силы предполагается, что режим работы является установившимся (М = const и ω = сonst). При наличии зазора между цапфой и втулкой цапфа вкатывается по поверхности отверстия в направлении противоположном вращению вала, то есть поворачивается относительно исходного положения на величину угла трения ρ.

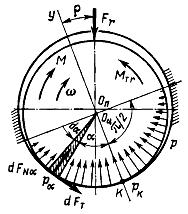
Для неприработанных опор момент трения равен:

,

где - приведенный коэффициент трения;

Введем обозначение: ,

а) ξ = 1,57 – для неприработанных опор (на цапфе и втулке существуют неровности, создающие эффект торможения);

б) ξ = 1,27 – для приработанных опор;

в) ξ = 1 – для опор с большим радиальным зазором.

11.3.2 Расчет осевого момента трения

При определении момента трения опоры от осевой нагрузки F_a, воспринимаемой кольцевой пятой, предполагаем распределенным равномерно давление по всей ширине кольца с диаметрами d₁ и d. На пяте выделяем кольцевую зону с текущим радиусом ρ шириной dρ.

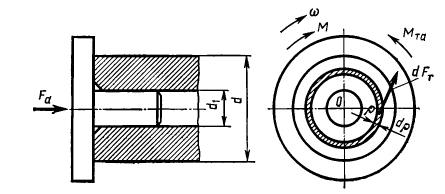
Момент трения на кольцевой пяте равен:

Для сплошной пяты d₁ = 0, тогда

Лекция № 12

12.1 Механические передачи.

Механизмы, предназначенные для передачи и преобразования энергии, моментов, сил, перемещений, скоростей от ведущего элемента к ведомому называются передачами. Большинство приборных устройств представляют собой комплексы, в которых сочетаются электрические, пневматические, оптические и прочие измерительные цепи с передаточными механизмами.

К конструкциям передаточных механизмов предъявляются следующие требования:

- заданной точности преобразования движения;

- достаточной прочности и жесткости элементов механизма при передаче усилий или моментов;

- высокого коэффициента полезного действия (КПД);

- простоты и надежности регулировки;

- малой чувствительности к колебаниям температуры и динамическим нагрузкам;

- технологичности конструкции, минимизации габаритов и стоимости изготовления.

При разработке конструкции передаточного механизма конструктор-проектировщик должен искать компромиссные решения сбалансированного соотношения перечисленных требований.

12.2 Классификация по признакам

Все элементарные передаточные механизмы можно классифицировать по ряду признаков.

К ним относятся конструктивный и кинематический признаки, признаки по виду преобразования движения, по преобразованию скорости и по принципу действия.

По конструктивному признаку - зубчатые, червячные, винтовые, с гибкими звеньями, фрикционные, рычажные, кулачковые и прерывистого движения.

По виду преобразования движений:

- вращательного во вращательное (зубчатые, червячные, кулачковые с качающимся роликом);

- вращательного в поступательное (реечная, винтовая, кулачковая с поступательно движущимся толкателем, кривошипно- шатунная передачи);

- поступательного во вращательное (реечная, синусная и тангенсная передачи);

- поступательное в поступательное (двойные синусная и тангенсная передачи).

По преобразованию скорости движения:

- с постоянным отношением скоростей (зубчатая, фрикционная, червячная передачи);

- с переменным отношением скоростей (вариаторы).

Передачи с переменным отношением скоростей одно из звеньев находится в равномерном движении, а другое подчиняется заданному закону. К этой же группе относятся также передачи прерывистого движения (храповая передача, передача с мальтийским крестом).

В зависимости от назначения и условий работы передачи делят на силовые и кинематические.

Силовые передачи передают значительные мощности, работают в условиях значительных скоростей, динамических нагрузок и при экстремальных условиях эксплуатации. Для них основными расчётами являются расчёты на прочность. Расчёт производят по условию обеспечения заданной мощности. Кроме того, к ним предъявляются требования по надёжности, долговечности и заданной точности.

Кинематические передачи имеют малую нагрузку, к ним предъявляются требования по точности, быстродействию и габаритам.

В зависимости от принципа действия передачи делятся на передачи трением и передачи зацеплением.

Передачи трением делятся на фрикционные передачи посредством взаимодействия твёрдых тел (шкивы, диски, валики, сферические и конические поверхности) и передачи гибкими связями, содержащие промежуточные элементы, осуществляющие гибкую связь (ремень, шнур, пассик).

Передачи зацеплением – зубчатые и червячные.

Кроме того, существуют передачи, использующие как трение, так и зацепление: цепные, тросиковые, передачи зубчатым ремнём.

К передачам также относятся устройства, в которых гибкие связи жёстко соединены со шкивами, а также рычажно-шарнирные, кулачковые, поводковые передачи.

Проектирование передач начинают с разработки кинематических схем, которые дают представление как о принципе работы данной передачи, так и о ее конструкции. Условное изображение передачи на кинематических схемах допускают плоское или пространственное изображение этих передач в соответствии с ГОСТ.

12.3. Кинематические характеристики передач Кинематические исследования передач проводят для оценки кинематических характеристик и последующего решения задач динамики. Цель такого исследования – изучение движения звеньев механизмов независимо от действующих сил. При этом определяют положение элементов передачи, линейные и угловые скорости, передаточные отношения. Исходными данными служат размеры конструкции элементов.

В передачах, в которых вращательное движение преобразуется во вращательное, передаточным отношением i называется отношение угловых скоростей ведущего и ведомого звеньев передачи. Его записывают с индексацией, показывающей, в каком направлении происходит движение:

i₁₂ = n₁/n₂ = __ - для редуктора;

i₂₁ = n₂/n₁ = ₂_{1 ­}– для мультипликатора.

Передаточное отношение, определяемое отношением угловых скоростей, - величина безразмерная. В случае, когда передача движения сопровождается изменением его вида, например, поступательного во вращательное или наоборот, передаточное отношение является величиной размерной.

Передаточное отношение может быть постоянным или переменным.

В общем случае передаточное отношение выражают через отношение частных производных от перемещения по обобщённой координате:

.

Это позволяет заменить отношение скоростей отношением соответствующих перемещений.