Министерство образования и науки Российской Федерации
ГОУ
ВПО «
Кафедра
«
ВЫПОЛНИЛИ студент группы ПС-204 Счастливцев Е.В. студент группы ПС-203 Люкшин Е.О. 24 марта 2012 г. ПРОВЕРИЛ д.т.н. Лапин А.П. 24 марта 2012 г.
Условие задачи.
Дана система линейных уравнений, найти её корни используя метода Гаусса.
Оглавление
1 Общие сведения 3
2 Функциональное назначение 4
3 Описание логической структуры 6
4 Используемые технические средства 13
5 Вызов и загрузка 13
6 Входные данные 13
7 Выходные данные 14
8 Контрольные примеры 14
9 Тескт программы 26
Общие сведения
Программа именуется «реализация метода Гаусса». Для нормального функционирования программы необходимо следующее программное обеспечение:
операционная система MS-Windows XP;
Пакет программ Microsoft Visual Studio 2010.
Программа написана на языке высокого уровня Си.
Функциональное назначение
Программа предназначена для решения системы линейных уравнений методом Гаусса.
Описание метода:
Пусть исходная система порядка n выглядит следующим образом:
Первое,
что надо сделать – проверить коэффициенты
на равенство нулю, по меньшей мере хотя
бы один из коэффициентов должен быть
отличен от нуля. Если они все равны нулю,
то у системы нет решений Предположим,
что 1 из коэффициентов отличен от нуля,
но первый коэффициент (
равен нулю, тогда нужно делать перестановку
уравнений, пока
не будет отличен от нуля.
Затем
вводим множитель
=
,
умножаем первое уравнение системы на
и вычитаем из второго уравнения, тогда
получим новое второе уравнение:
;
где j=1, …, n
– номер столбца.
Потом тоже самое проделываем с другими строками:
;
где i=3,…,n
– номер уравнения из которого исключается
неизвестное; j=1,…,n
– номер столбца.
В результате получаем новую систему:
Новая
система полностью эквивалентна старой
системе, за исключением того что во всех
строках системы, кроме первой, отсутствует
,
то есть мы имеем n-1 уравнение
с n-1 неизвестным.
Затем проделываем те же самые действия с новой системой порядка n-1:
Проверяем
коэффициенты
,
где k<n –
номер вычитаемой строки, на равенство
нулю. Если они все равны нулю, то у системы
нет решений. Если коэффициент
не равен нулю, то оставляем все как есть,
если же он равен нулю, но хотя бы 1
коэффициент отличен от нуля, тогда нужно
делать перестановку уравнений, пока
не будет отличен от нуля.
Затем
вводим множители
,
где i=k+1,…,n,
k-е уравнение системы на
этот множитель и вычитаем из i-го
уравнения, тогда элементы этого уравнения
буду находиться по формулам:
где
i=k+1,…,n
– номер уравнения, которое вычитается
из остальных, j=k,…,n
– номер столбца.
В результате получим систему вида:
Процедура приведения системы к треугольному виду называется прямым ходом.
Затем
мы проверяем коэффициент
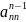и элемент
на равенство нулю, если они оба равны
нулю, то у системы бесконечно много
решений, если
,
то у системы нет решений, если
отличен
от нуля, то у системы единственное
решение, и в этом случае корни вычисляются
следующим образом:
;
,
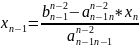и так далее.
Процедура нахождения корней называется обратным ходом.
Функциональные ограничения:
Порядок системы n должен быть целым положительным числом;
Описание логической структуры
Описание логической структуры программы представлено схемой алгоритма.
Схема алгоритма функции main().
Схема алгоритма функции vvodstr(a[100], k).
Схема алгоритма функции preobr(a[100], n).
3.1 Руководство пользователя
После запуска программы на выполнение на экране появится сообщение:
«Введите порядок системы: n=», - Пользователю необходимо ввести значение n на клавиатуре и завершить ввод клавишей <Enter> (Рисунок 1).
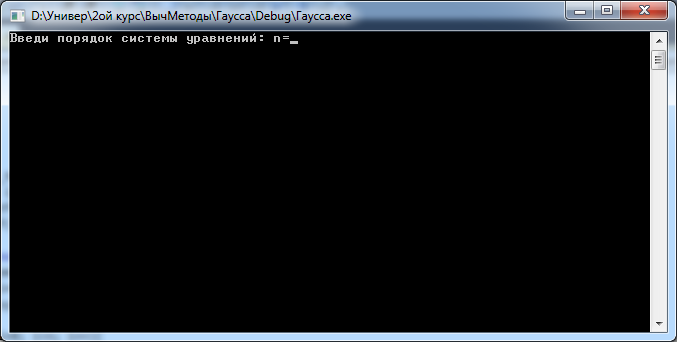
Рисунок 1
После этого на экране появится сообщение: «Введите коэффициент a11 системы: », - Пользователю необходимо ввести нужно значение на клавиатуре и завершить ввод клавишей <Enter>. Аналогично Пользователь должен ввести остальные элементы системы (Рисунок 2).
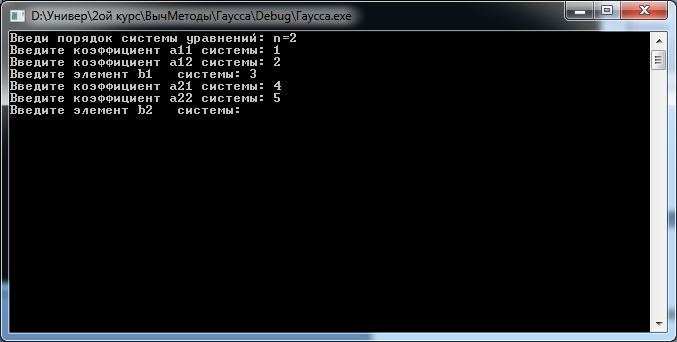
Рисунок 2
Затем на экране появится введенная Пользователем система и сообщение: «Нажмите Y, если хотите редактировать систему, или N, чтобы продолжить», - Пользователю необходимо нажать клавишу <Y>, чтобы редактировать систему, или клавишу <N>, чтобы продолжить .
Если Пользователь нажал клавишу <Y>, то на экране появится сообщение:
«Введите номер уравнения, в котором хотите редактировать элемент (i>0, i<n+1): i=», - Пользователю необходимо ввести номер уравнения (положительно число, не больше порядка матрицы) на клавиатуре и завершить ввод нажатием клавиши <Enter>.
Затем на экране появится сообщение: «Введите номер этого элемента в уравнении (j>0, j<n+2): j=», - Пользователь должен ввести номер элемента, который он хочет редактировать, в уравнении (положительно число, не больше числа n+1) на клавиатуре и завершить ввод нажатием клавиши <Enter>. Если номера введены корректно, то Пользователю будет предложено ввести новое значение редактируемого элемента (Рисунок 3). Затем снова будет предложено нажать клавишу <Y>, чтобы редактировать систему, или клавишу <N>, чтобы продолжить.
Рисунок 3
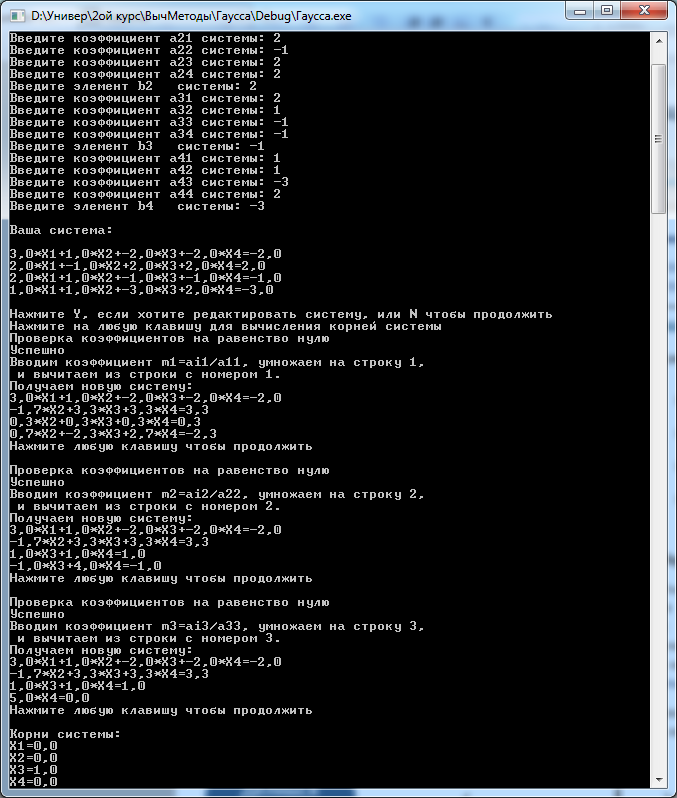
Если Пользователь нажал клавишу <N>, то на экране появится сообщение: «Нажмите на любую клавишу для вычисления корней», - Пользователю необходимо нажать на любую клавишу на клавиатуре для начала процедуры вычисления корней. Затем, если у системы есть решения, программа будет приводить матрицу системы к треугольному виду, и потом на экране появится ответ (Рисунок 4).
После этого Пользователю будет предложено сделать выбор: закрыть программу (нажав на клавишу <Esc>) или запустить заново (нажав любую другую клавишу).
Рисунок 4
3.2 Руководство программиста
В программе использованы следующие процедуры и функции:
А) vyvod() – функция для вывода системы уравнений.
Входные данные:
Целочисленная переменная n (тип int) – порядок системы;
матрица действительных элементов system[ ][ ] (тип double) – расширенная матрица системы.
Выходные данные: отсутствуют.
Вызывается из main() и из vychislenie().
Б) vychislenie() – функция для вычисления корней системы методом Гаусса.
Входные данные:
Целочисленная переменная n (тип int) – порядок системы;
массив действительных элементов x[] (тип double) – содержит корни системы;
матрица действительных элементов system[ ][ ] (тип double) – расширенная матрица системы.
Выходные данные: отсутствуют.
Вызывается из main().
Используемые технические средства
Для создания программы использовался компьютер на платформе ЭВМ IBM PC, с процессором Intel Pentium 4, тактовой частотой 3,06Ггц, оперативной памятью 512Мб, под управлением операционной системы Windows XP.
Вызов и загрузка
Для загрузки данной программой необходимо запустить файл «Гаусса.cpp» из среды Microsoft Visual Studio. На экране появится текст программы. Для запуска программы на исполнение пользователю необходимо нажать комбинацию клавиш Ctrl+F5. Вызов программы производится с жесткого диска. Объем программы составляет 28,5 Кбайт.
Входные данные
Входными данными являются:
Целая переменная n (тип int) – порядок системы;
матрица действительных элементов system[ ][ ] (тип double) – матрица системы.
Выходные данные
Матрица действительных элементов system[ ][ ] (тип double) – матрица системы;
массив действительных элементов x[ ] (тип double) – корни системы.
Контрольные примеры
Пример 1:
Проведём следующие действия:
Из строки № 2 вычтем строку № 1 (Строка 2 - строка 1);
из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 - 2 × строка 1);
из строки № 4 вычтем строку № 1 (Строка 4 - строка 1).
Получим:
Проведём следующие действия:
К строке № 3 прибавим строку № 2 (Строка 3 + строка 2);
строку № 4 поделим на 3 (Строка 4 = строка 4 / 3).
Получим:
Проведём следующие действия:
Строку № 4 поставим на место строки № 2;
строку № 3 поставим на место строки № 4;
строку № 2 поставим на место строки № 3.
Получим:
Проведём следующие действия:
К строке № 3 прибавим строку № 2 умноженную на 6 (Строка 3 + 6 × строка 2).
Получим:
Теперь начинаем вычисление корней:
;
;
;
=1-2+1-2=-2.
Получаем ответ:
Результат выполнения программы:
Пример 2:
Проведём следующие действия:
К строке №2 прибавим строку №1, умноженную на -2 (Строка 2 + (-2) × строка 1);
к строке №3 прибавим строку №1, умноженную на -4 (Строка 3 + (-4) × строка 1);
к строке №4 прибавим строку №1, умноженную на -5 (Строка 3 + (-4) × строка 1).
Получим:
Проведём следующие действия:
К строке №3 прибавим строку №2, умноженную на -1 (Строка 3 + (-1) × строка 2).
Получим:
В
третьей строке все элементы
равны нулю, а элемент
не
равен нулю, значит система не имеет
решений.
Ответ: решений нет.
Результат выполнения программы:
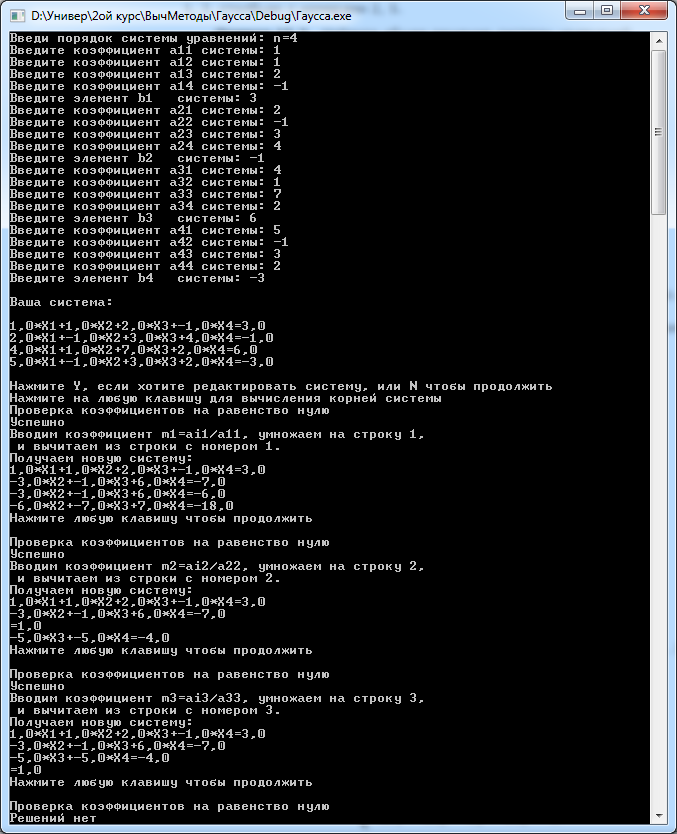
Пример 3:
Проведём следующие действия:
К строке №2 прибавим строку №1, умноженную на -2 (Строка 2 + (-2) × строка 1);
к строке №3 прибавим строку №1, умноженную на -4 (Строка 3 + (-4) × строка 1);
к строке №4 прибавим строку №1, умноженную на -5 (Строка 3 + (-4) × строка 1).
Получим:
Проведём следующие действия:
К строке №3 прибавим строку №2, умноженную на -1 (Строка 3 + (-1) × строка 2).
Получим:
В третьей строке все элементы равны нулю, значит система имеет бесконечно много решений.
Результат выполнения программы:
Пример 4:
Проведём следующие действия:
Поменяем местами строку № 1 и строку № 4.
Получим:
Проведём следующие действия:
Из строки № 2 вычтем строку № 1 умноженную на 2 (Строка 2 - 2 ×
строка 1);
из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 - 2 ×
строка 1);
из строки № 4 вычтем строку № 1 умноженную на 3 (Строка 4 - 3 ×
строка 1).
Получим:
Проведём следующие действия:
Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1);
поменяем местами строку № 2 и строку № 3.
Получим:
Проведём следующие действия:
К строке № 3 прибавим строку № 2 умноженную на 3 (Строка 3 + 3 × строка 2);
к строке № 4 прибавим строку № 2 умноженную на 2 (Строка 4 + 2 × строка 2).
Получим:
Проведём следующие действия:
Строку № 4 поделим на -3 (Строка 4 = строка 4 / -3);
поменяем местами строку № 3 и строку № 4.
Получим:
Проведём следующие действия:
К строке № 4 прибавим строку № 3 умноженную на 7 (Строка 4 + 7 × строка 3).
Получим:
Теперь начинаем вычисление корней:
;
;
;
Получаем ответ:
Результат выполнения программы:
