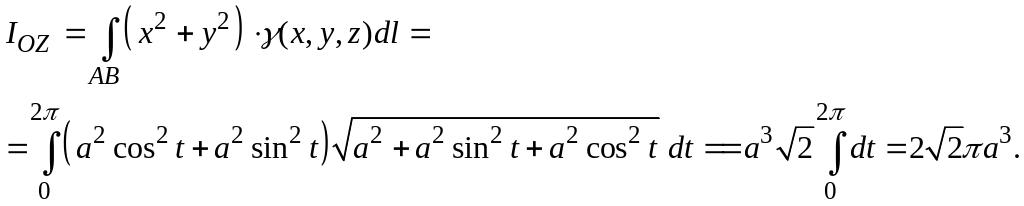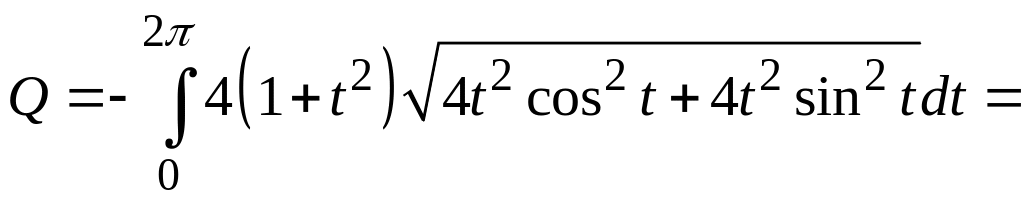2) Обчислення повного заряду, розташованого на матеріальній кривій

Повний заряд , розташований на матеріальній кривій , що задана рівнянням , де – неперервна функція на проміжку , а лінійна щільність (густина) заряду в кожній її точці визначається неперервною функцією , визначається за формулою:

. (5.14)

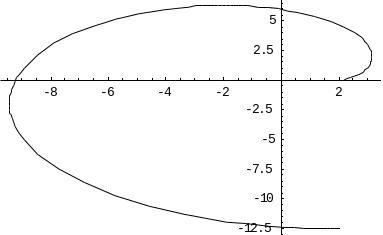
Приклад 6. Обчислити електричний заряд лінії, заданої рівняннями (рис. 5.9), якщо її густина заряду .

Розв’язання.

Рис. 5.9.

За формулою (5.14) статичний електричний заряд плоскої лінії . Враховуючи те, що , , а , інтеграл запишемо так:

3) Статичні моменти та координати центра мас.

Нехай плоска матеріальна крива має щільність (густину) . Статичний момент відносно осі визначається формулою

, (5.15)

відносно осі –

. (5.16)

Аналогічно, статичні моменти кривої у просторі відносно координатних площин визначаються формулами:

. (5.17)

Координати центра мас

а) для плоскої кривої масою : ; (5.18)

б) для кривої у просторі масою :

. (5.19)

Приклад 7. Знайти центр мас чверті однорідного кола .

Розв’язання. Однорідність матеріальної кривої означає, що в кожній її точці щільність (густина) . Можна вважати, що . Тоді маса кривої дорівнює її довжині . Статичний момент .

Очевидно, що для даної кривої , тому координати центра мас дорівнюють:

.

4) Перша формула Гульдіна

Означення. Центроїд лінії (нематеріальна, геометрична лінія) – центр мас цієї лінії з довільною сталою щільністю. Якщо крива знаходиться у площині , то центроїд має координати

.

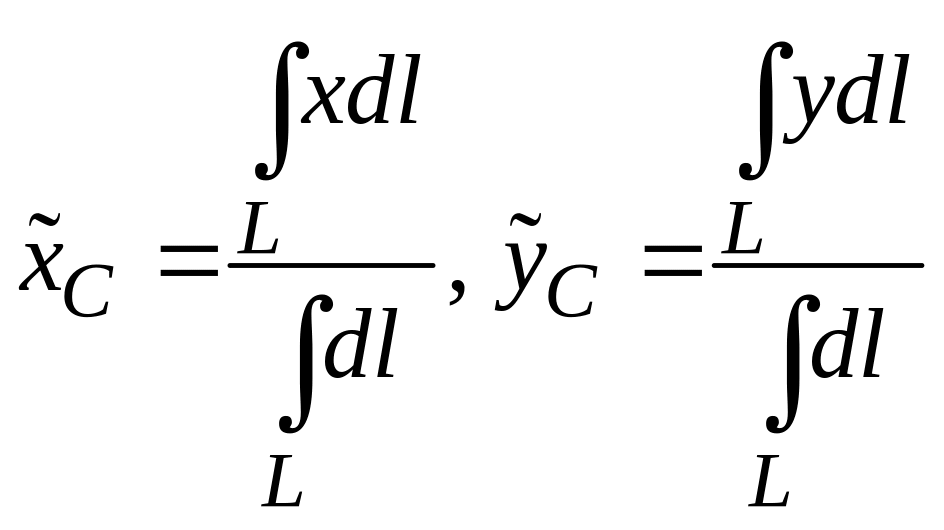Площа поверхні, утвореної обертанням навколо осі кривої, що розташована у площині осі обертання по одну сторону від неї, дорівнює добутку довжини цієї кривої на довжину кола, яке описує при обертанні центроїд кривої

, (5.20)

де – довжина кривої, – відстань від центроїда до осі обертання.

4) Моменти інерції.

Момент інерції кривої , яка має лінійну щільність , відносно певної осі дорівнює

, (5.21)

де – квадрат відстані від точки до осі .

Моменти інерції плоскої кривої , яка має щільність (густину) , відносно координатних осей обчислюються за формулами:

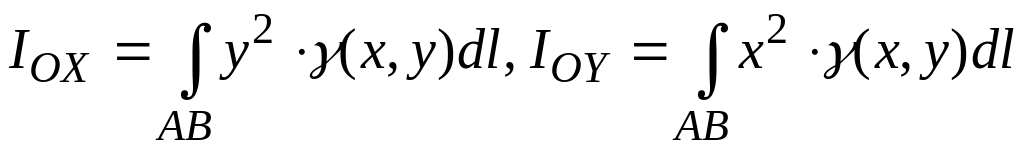, (5.22)

Момент інерції відносно початку координат

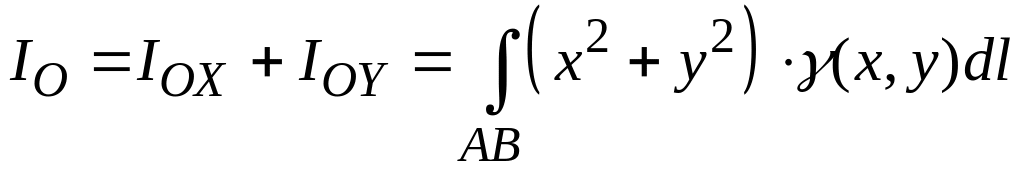. (5.23)

В випадку кривої у просторі моменти інерції відносно координатних осей та початку координат обчислюються

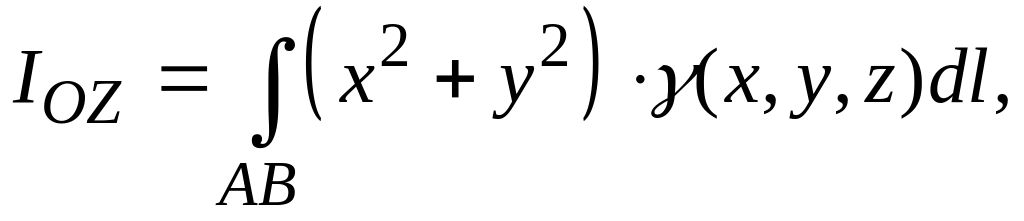(5.24)

. (5.25)

Приклад 8. Знайти момент інерції відносно осі однорідної гвинтової лінії ( ), яка задається рівняннями: (рис. 5.2).

Розв’язання. За формулою (5.24)