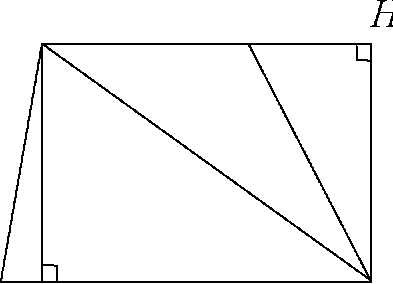
Вопрос № 2 Формула площади трапеции. Запись, вывод

Высотой трапеции называется перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание.

B

C

'1

Теорема. Площадь трапеции равна произведению полусуммы её основа­ний на высоту.

Дано: ABCD - трапеция,

D

ВС и AD - основания, BH - высота. Доказать: S_ABCD = 1 (AD BC )• BH.

A H

Доказательство

Диагональ BD разделяет трапецию ABCD на D ABD и D BCD, поэтому по свойству площадей S_ABCD = S_ABD + S_BCD.

Таким образом, S

ABCD

В D ABD AD - основание, ВН - высота, поэтому S_ABD = 1 AD • BH. В D BCD ВС - основание, DHi - высота, поэтому S_BCD = 2 BC • DH₁. Так как BH = DHj, то S_BCD

2 BC • BH. 2 AD • BH + 2 BC • BH, Sabcd = 2 (AD + BC )• BH.

Итак, площадь трапеции равна произведению полусуммы её оснований на высоту.

соту:

Ч.т.д.

Площадь трапеции равна произведению полусуммы её оснований на вы-

S = 2 (a + b) • h, a и b - основания трапеции, h - её высота.

Площадь трапеции равна половине произведения её диагоналей на синус угла между ними: S = 2 d₁d₂ sin а, di и d₂ - диагонали трапеции, a - угол между ними.

1. Теорема об угле, вписанном в окружность.

2. Формула площади параллелограмма. Запись, вывод.

Вопрос № 1

Теорема об угле, вписанном в окружность. Следствия

Угол, вершина которого лежит на окружности, а стороны пересекают ок­ружность, называется вписанным углом.

На рисунке 1 Z АВС вписанный, и АС расположена внутри этого угла. В таком случае говорят, что вписанный Z АВС опирается на и АС.

Теорема. Вписанный угол измеряется половиной дуги, на которую опирается.

Дано: ZАВС - вписанный угол, опирающийся на и АС. Доказать: ZАВС = ¹ иАС.

Доказательство

Рассмотрим три возможных случая расположения луча ВО относительно Z АВС.

I случай

Луч ВО совпадает с одной из сторон Z АВС, напри­мер со стороной ВС (рис. 1). В этом случае и АС меньше полуокружности, поэтому Z АОС = и АС. ZАОС - внеш­ний угол D АОВ при вершине О, поэтому он равен сумме двух внутренних углов треугольника, не смежных с ним, т.е. Z АОС =Z 1 + Z 2. Но D АОВ - равнобедренный, т.к. ОА = ОВ, как радиусы, значит, Z 1 = Z 2, как углы при основании равнобедренного треугольника. Следователь­но,^ АОС =Z 1 + Z 2 = 2Z 1 = 2Z АВС, отсюда^ АВС

B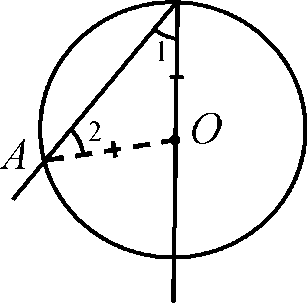

C

Рис.1

=¹ ZАОС. А т.к. ZАОС = и АС, то Z АВС =¹ иАС. 2 ' 2

II случай

Луч ВО делит Z АВС на два угла (рис. 2). В этом случае луч ВО, пересекает и АС в некоторой точке D, которая разделяет и АС на две дуги: и AD и и DС, а Z АВС на два угла: Z ABD и Z DВС. По доказанному

B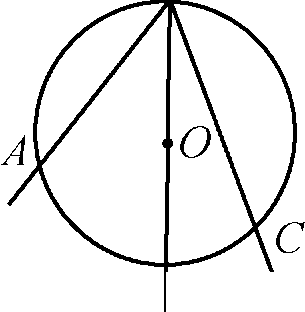

выше, ZАВD =¹ и АD, Z DВС =¹ и СD.

и АВ + 1 и DG = 2

D Рис.2

22

Значит, ZАВС = ZMD + Z DВС

¹ (и АD + и DQ = ¹ и АС, т.е. Z АВС = ¹ и АС.

III случай

Луч ВО не делит Z АВС на два угла и не сов­падает со сторонами этого угла (рис. 3). В этом случае и АС = и AD - и CD.

Z АВС = Z ABD - Z CBD = 1 и AD - 1 и CD =

B

2 2

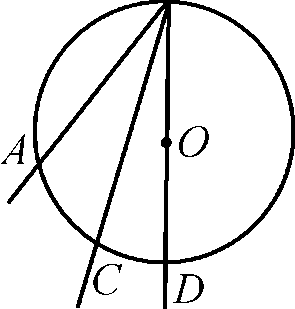
¹ ( и AD - и CD) = 1 и АС, т.е. Z АВС = ¹ и АС.

2

Рис.3

Итак, вписанный угол измеряется половиной дуги, на которую опирается.

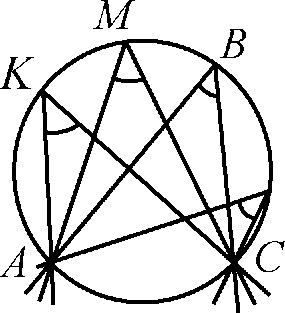
Рис.4

Ч.т.д.

Следствие 1

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Z АКС = Z АМС = Z АВС = ..., так как они опираются на одну и ту же и АС (рис. 4).

Следствие 2

Вписанный угол, опирающийся на полуокруж­ность, - прямой.

M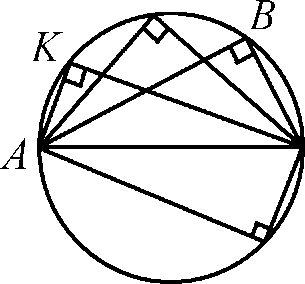

C

ZАКС = ZАМС = ZАВС = ... 90°, так как они опираются на диаметр АВ (рис. 5).

Рис.5

Замечание. Так как градусная мера дуги равна градусной мере соответст­вующего центрального угла, то теорему о вписанном угле можно сформулиро­вать следующим образом: угол, вписанный в окружность, равен половине соот­ветствующего центрального угла, т.е.

ZАВС = ¹Z АОС.

Вопрос № 2

Формула площади параллелограмма. Запись, вывод

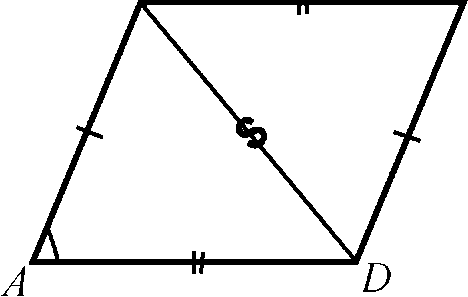
Теорема. Площадь параллелограмма равна произведению двух его смеж­ных сторон на синус угла между ними.

BC

Дано: ABCD - параллелограмм.

Доказать: S_AABCD = АВ • AD sin А.

Доказательство

В параллелограмме ABCD проведем диагональ BD, и рассмотрим полу­чившиеся треугольники ABD и CDB.

АВ = CD, ВС = AD, т.к. в параллелограмме противолежащие стороны равны; BD - общая сторона. Следовательно, A ABD = A CDB по III признаку равенства треугольников (по трем сторонам).

Равные фигуры имеют равные площади, поэтому S_{A ABD} = S_{A CDB}.

По свойству площадей площадь параллелограмма равна сумме площадей треугольников, из которых он составлен, поэтому S_ABCD = S_AABD + S_{A CDB} = 2 S_AABD.

Так как площадь треугольника равна половине произведения двух его сторон на синус угла между ними, то

S_ABCD = 2• 2АВ • AD sin А = АВ • AD sin А.

Итак, площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Ч.т.д.