
- •Вопрос № 1 Второй признак равенства треугольников
- •Вопрос № 2 Прямоугольник. Определение и свойства
- •Доказательство
- •Окружность. Определение, взаимное расположение прямой и окружности
- •Вопрос № 2 Формула длины окружности. Запись, вывод
- •Вопрос 2 Формула для радиуса окружности, описанной около правильного w-угольника. Запись, вывод
- •Теорема о соотношении между сторонами треугольника (неравенство треугольника)
- •Доказательство
- •Билет № 9
- •Вопрос № 1 Теорема о средней линии треугольника
- •Доказательство
- •Вопрос № 2 Формула площади круга. Запись, вывод
- •2R, то получаем формулу для вычисления площади круга
- •Билет № 10
- •Вопрос № 1 Теорема о средней линии трапеции
- •Доказательство
- •Площадь треугольника через радиус описанной окружности
- •Площадь треугольника через радиус вписанной окружности
- •Вопрос № 2 Формула площади трапеции. Запись, вывод
- •Доказательство
- •Билет № 14
- •Вопрос № 1 Признаки параллелограмма
- •Признаки параллелограмма
- •Вопрос № 1 Теорема Фалеса
- •Доказательство
- •Вопрос № 2 Осевая симметрия. Определение, примеры
- •Примеры фигур, обладающих осевой симметрией
- •Билет № 16 Теорема Пифагора
- •Вопрос № 1 Теорема синусов
- •Доказательство
- •Вопрос № 1 Теорема косинусов
- •Доказательство
- •Вопрос № 2 Биссектриса угла. Определение, свойство
- •Доказательство
- •Билет № 19
- •Вопрос № 1 Первый признак подобия треугольников
- •Доказательство
- •Вопрос № 2 Построение середины данного отрезка
- •Построение
- •Билет № 20
- •Вопрос № 1 Второй признак подобия треугольников
- •Вопрос № 2 Построение биссектрисы данного угла
- •Построение
- •Билет № 21
- •Вопрос № 1 Третий признак подобия треугольников
- •Вопрос № 2 Построение угла, равного данному
- •Построение
- •Билет № 22
- •Вопрос № 1 Вывод уравнения прямой
- •Вопрос № 2 Перпендикулярные прямые. Определение, построение прямой, перпендикулярной данной
- •Построение
- •Доказательство
- •Билет № 23
- •Вопрос № 1 Вывод уравнения окружности
- •Билет № 24
- •Вопрос № 2 Вертикальные углы. Определение, свойство
- •Вопрос № 2 Скалярное произведение двух векторов. Определение, свойства
Площадь треугольника через радиус описанной окружности
S abc s =
4R
где а, b, с - стороны треугольника, R - радиус описанной окружности.
Площадь треугольника через радиус вписанной окружности
S = rp,
р - полупериметр треугольника, r - радиус вписанной окружности.
Билет № 11
Теорема об окружности, описанной около треугольника.
Тригонометрические тождества. Примеры, доказательства.
Вопрос № 1
Теорема об окружности, описанной около треугольника
Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник - вписанным в эту окружность.
Теорема. Около любого треугольника можно описать окружность.
Дано: D ABC.
Доказать: около D ABC можно описать окружность.
C
Доказательство
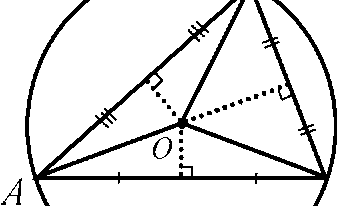
Рассмотрим произвольный D ABC. Проведём серединные перпендикуляры к сторонам треугольника, точку их пересечения обозначим буквой О. Соединим точку О с вершинами A, B и C.
Так как точка пересечения серединных перпендикуляров равноудалена от вершин D ABC, то OA = ОВ = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника, и значит, является описанной около D ABC.
Итак, около любого треугольника можно описать окружность, центром которой является точка пересечения серединных перпендикуляров к сторонам треугольника, а радиусом - расстояние от центра окружности до любой вершины треугольника.
Ч.т.д.
Замечание 1. Около треугольника можно описать только одну окружность.
Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудалён от вершин треугольника и, значит, совпадает с точкой О - точкой пересечения серединных перпендикуляров к сторонам треугольника. Так как радиус каждой окружности равен расстоянию от точки О до вершин треугольника, то радиусы окружностей совпадают. Следовательно, эти окружности совпадают.
Вопрос № 2
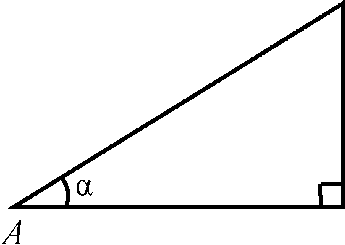
С
в
D АВС - прямоугольный, Z С - прямой,
ВС - катет, противолежащий углу a, АС - катет, прилежащий углу a.
Синусом острого угла прямоугольного треугольника называется отноше-
ВС
ние противолежащего катета к гипотенузе: sin а = ^в ■
Косинусом острого угла прямоугольного треугольника называется отно-
АС
шение прилежащего катета к гипотенузе: cos а = ав ■
Тангенсом острого угла прямоугольного треугольника называется отно-
ВС
шение противолежащего катета к прилежащему катету: tga
АС
Разделим синус угла a на косинус угла a:
=
tgа, т.е.
cos а АВ АВ АВ АС АС
cosa
ф
0, т.к.
a
-
острый угол.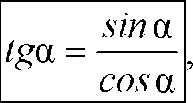
Котангенсом острого угла прямоугольного треугольника называется от-
АС
ношение прилежащего катета к противолежащему катету: ctgа =
ВС
Разделим косинус угла a на синус угла a:
^а,
т.е.
sin а АВ АВ АВ ВС ВС
![]()
,
sina
ф
0, т.к.
a
-
острый угол.
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы, тангенсы и котангенсы этих углов равны.
• 2 2 1
sin а + cos а = 1 - основное тригонометрическое тождество, докажем его для острого угла прямоугольного треугольника.
• 2 , 2 sin a + cos a =
v
AB y
v AB y
по теоремеПифагора
=
1, т.е.
AB
AB
AB 2 AB 2
sin2 a + cos2 a = 1
Умножим тангенс угла a на котангенс угла a:
=
1, т.е.
tga • ctga =
cos a sin a
22
sin
a cos
a
2
' 2 = 2 cos
a cos
a cos
a
Из формулы tga • ctga = 1 непосредственно вытекают следующие формулы:
1 |
|
1 |
tga = |
|
ctga = — |
ctga |
|
tga |
Разделим левую и правую часть основного тригонометрического тождества на cos2a ф 0:
sin2a + cos2a = 1 | : cos2a ф 0, 1
2 1
22
sin
a
cos
a
• 2
' ~2 = • 2 sin
a
sin
a
sin
a
cos 2 a
Разделим левую и правую часть основного тригонометрического тожде-
ства на sin a ф 0:
sin2a + cos2a = 1 | : sin2a ф 0, 1
21
1 + ctg 2 a =
sin2 a
Билет № 12
Теорема об окружности, вписанной в треугольник.
Формула площади трапеции. Запись, вывод.
Задача по теме «Геометрические преобразования».
Вопрос № 1
Теорема об окружности, вписанной в треугольник
Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник - описанным около этой окружности.
Теорема. В любой треугольник можно вписать окружность. B
Дано: D ABC.
C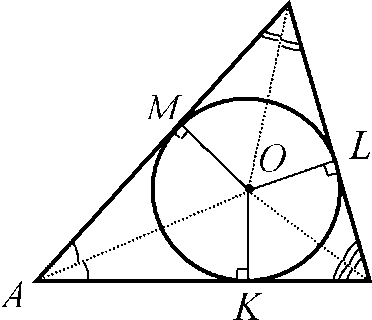
Доказательство
Рассмотрим произвольный D ABC. Проведём биссектрисы треугольника, точку их пересечения обозначим буквой О. Из точки О опустим перпендикуляры ОМ, OL и ОК соответственно к сторонам АВ, ВС и АС.
Так как каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон, то точка О равноудалена от сторон D ABC, т.е. ОМ = OL = ОК. Поэтому окружность с центром О радиуса ОК проходит через точки М, L и К. Стороны треугольника D ABC касаются этой окружности в точках М, L и К, так как они перпендикулярны к радиусам ОМ, OL и ОК. Значит, окружность с центром О радиуса ОК является вписанной в D ABC.
Итак, в любой треугольник можно вписать окружность, центром которой будет точка пересечения биссектрис треугольника, а радиусами - перпендикуляры, опущенные из центра окружности к сторонам треугольника.
Ч.т.д.
Замечание. В треугольник можно вписать только одну окружность.
Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудалён от сторон треугольника и, значит, совпадает с точкой О - точкой пересечения биссектрис треугольника. Радиус каждой окружности равен расстоянию от точки О до сторон треугольника. Так как из одной точки на прямую можно опустить только один перпендикуляр, то радиусы окружностей совпадают. Следовательно, эти окружности совпадают.
