
- •Вопрос № 1 Второй признак равенства треугольников
- •Вопрос № 2 Прямоугольник. Определение и свойства
- •Доказательство
- •Окружность. Определение, взаимное расположение прямой и окружности
- •Вопрос № 2 Формула длины окружности. Запись, вывод
- •Вопрос 2 Формула для радиуса окружности, описанной около правильного w-угольника. Запись, вывод
- •Теорема о соотношении между сторонами треугольника (неравенство треугольника)
- •Доказательство
- •Билет № 9
- •Вопрос № 1 Теорема о средней линии треугольника
- •Доказательство
- •Вопрос № 2 Формула площади круга. Запись, вывод
- •2R, то получаем формулу для вычисления площади круга
- •Билет № 10
- •Вопрос № 1 Теорема о средней линии трапеции
- •Доказательство
- •Площадь треугольника через радиус описанной окружности
- •Площадь треугольника через радиус вписанной окружности
- •Вопрос № 2 Формула площади трапеции. Запись, вывод
- •Доказательство
- •Билет № 14
- •Вопрос № 1 Признаки параллелограмма
- •Признаки параллелограмма
- •Вопрос № 1 Теорема Фалеса
- •Доказательство
- •Вопрос № 2 Осевая симметрия. Определение, примеры
- •Примеры фигур, обладающих осевой симметрией
- •Билет № 16 Теорема Пифагора
- •Вопрос № 1 Теорема синусов
- •Доказательство
- •Вопрос № 1 Теорема косинусов
- •Доказательство
- •Вопрос № 2 Биссектриса угла. Определение, свойство
- •Доказательство
- •Билет № 19
- •Вопрос № 1 Первый признак подобия треугольников
- •Доказательство
- •Вопрос № 2 Построение середины данного отрезка
- •Построение
- •Билет № 20
- •Вопрос № 1 Второй признак подобия треугольников
- •Вопрос № 2 Построение биссектрисы данного угла
- •Построение
- •Билет № 21
- •Вопрос № 1 Третий признак подобия треугольников
- •Вопрос № 2 Построение угла, равного данному
- •Построение
- •Билет № 22
- •Вопрос № 1 Вывод уравнения прямой
- •Вопрос № 2 Перпендикулярные прямые. Определение, построение прямой, перпендикулярной данной
- •Построение
- •Доказательство
- •Билет № 23
- •Вопрос № 1 Вывод уравнения окружности
- •Билет № 24
- •Вопрос № 2 Вертикальные углы. Определение, свойство
- •Вопрос № 2 Скалярное произведение двух векторов. Определение, свойства
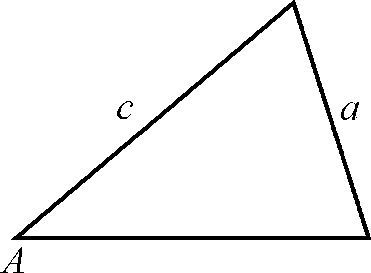
Вопрос № 1 Теорема синусов
Теорема. Стороны треугольника пропорциональны синусам противолежащих углов.
B
Дано: D АВС, ВС = а, АС = b, AB = c.
rr a b c
Доказать:
sin A sinB sinC
Доказательство
По теореме о площади треугольника
S = — absinC , S =— bcsinA , S =— acsinB . 2 2 2
Из первых двух равенств получаем ^ absinC = ^ bcsinA,
asinC = csinA \ : (sin AsinC) Ф 0, asinC csinA a c
sin AsinC sinAsin C sin A sin C Точно так же из второго и третьего равенств получаем
— acsinB = — bcsinA, asinB = bsinA \ : (sin AsinB ) Ф 0, 22
asinB bsinA a b sin AsinB sinAsinB sin A sinB
a c a b a b c Т ак как = и = , то
sin A sin C sin A sin B sin A sin B sin C Итак, стороны треугольника пропорциональны синусам противолежащих углов.
Ч.т.д.
b C
a b c
= 2 R,
sin A sin B sin C где R - радиус описанной окружности.
Вопрос № 2
Серединный перпендикуляр. Определение, свойство
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярна к нем. На рисунке 1 а - серединный перпендикуляр к отрезку АВ. Рис. 1
а
а 1 АВ, АО = ОВ
+
А
O
Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка (рис. 2). Рис. 2
а |
|
|
/ |
\.М |
|
|
1 , |
|
• 1 O |
|
|
В
Дано:
а 1 АВ, а П АВ = АО = ОВ, Ме
а. Доказать:
АМ = МВ.
О,
А
Доказательство
Если точка М совпадает с точкой О, то АМ = МВ, так как АО = ОВ.
Пусть Ми О - различные точки. Рассмотрим D ОАМи D ОВМ. Они прямоугольные, так как а 1 АВ. АО = ОВ по условию теоремы, ОМ - общая сторона. Следовательно, D ОАМ = D ОВМ по признаку равенства прямоугольных треугольников (по двум катетам).
В равных треугольниках соответствующие элементы равны, поэтому АМ = МВ.
Итак, каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Ч.т.д.
Верна и обратная теорема.
Теорема. Каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему (рис. 3).
Дано:
а
П АВ = О, АО = ОВ,
точка
N, АИ = ИВ. Доказать:
Ne
а, а 1 АВ.
а |
|
|
|
|
п 1 ■'■■• |
• 1 O |
|
А
В
Доказательство
Если точка Ne АВ, то она совпадает с точкой О - серединой отрезка АВ и поэтому N e а.
Пусть N € АВ. Рассмотрим D ANB. Он равнобедренный, так как AN = NB. Отрезок NO - медиана D ANB, а следовательно, и высота, так как медиана равнобедренного треугольника, проведённая к основанию является и высотой.
Таким образом, NO L АВ, поэтому ON и а совпадают, и, значит, N e а.
В равных треугольниках соответствующие элементы равны, поэтому АМ = МВ.
Итак, каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Ч.т.д.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Точка пересечения серединных перпендикуляров к сторонам треугольника - замечательная точка треугольника, так как она является центром окружности, описанной около треугольника.
Теорема косинусов.
Биссектриса угла. Определение, свойство.
