
- •Вопрос № 1 Второй признак равенства треугольников
- •Вопрос № 2 Прямоугольник. Определение и свойства
- •Доказательство
- •Окружность. Определение, взаимное расположение прямой и окружности
- •Вопрос № 2 Формула длины окружности. Запись, вывод
- •Вопрос 2 Формула для радиуса окружности, описанной около правильного w-угольника. Запись, вывод
- •Теорема о соотношении между сторонами треугольника (неравенство треугольника)
- •Доказательство
- •Билет № 9
- •Вопрос № 1 Теорема о средней линии треугольника
- •Доказательство
- •Вопрос № 2 Формула площади круга. Запись, вывод
- •2R, то получаем формулу для вычисления площади круга
- •Билет № 10
- •Вопрос № 1 Теорема о средней линии трапеции
- •Доказательство
- •Площадь треугольника через радиус описанной окружности
- •Площадь треугольника через радиус вписанной окружности
- •Вопрос № 2 Формула площади трапеции. Запись, вывод
- •Доказательство
- •Билет № 14
- •Вопрос № 1 Признаки параллелограмма
- •Признаки параллелограмма
- •Вопрос № 1 Теорема Фалеса
- •Доказательство
- •Вопрос № 2 Осевая симметрия. Определение, примеры
- •Примеры фигур, обладающих осевой симметрией
- •Билет № 16 Теорема Пифагора
- •Вопрос № 1 Теорема синусов
- •Доказательство
- •Вопрос № 1 Теорема косинусов
- •Доказательство
- •Вопрос № 2 Биссектриса угла. Определение, свойство
- •Доказательство
- •Билет № 19
- •Вопрос № 1 Первый признак подобия треугольников
- •Доказательство
- •Вопрос № 2 Построение середины данного отрезка
- •Построение
- •Билет № 20
- •Вопрос № 1 Второй признак подобия треугольников
- •Вопрос № 2 Построение биссектрисы данного угла
- •Построение
- •Билет № 21
- •Вопрос № 1 Третий признак подобия треугольников
- •Вопрос № 2 Построение угла, равного данному
- •Построение
- •Билет № 22
- •Вопрос № 1 Вывод уравнения прямой
- •Вопрос № 2 Перпендикулярные прямые. Определение, построение прямой, перпендикулярной данной
- •Построение
- •Доказательство
- •Билет № 23
- •Вопрос № 1 Вывод уравнения окружности
- •Билет № 24
- •Вопрос № 2 Вертикальные углы. Определение, свойство
- •Вопрос № 2 Скалярное произведение двух векторов. Определение, свойства
Вопрос № 1 Теорема Фалеса
Теорема. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Дано: li, lf, А1,А2, А3, А4, ...е 1 АА = А2А3 = А3А4 = ...;
А1В1 || А2В2 || А3В3 || А4В4\\ Bi,В2, В3, В4, ...е 2
Доказательство
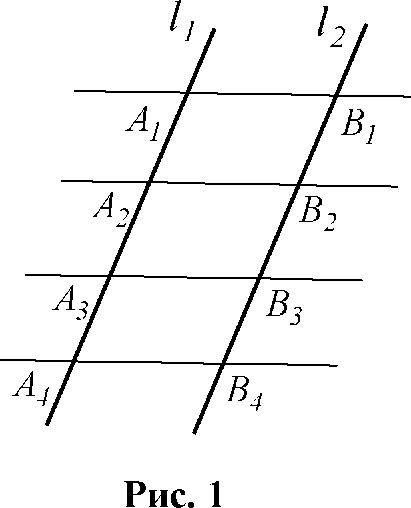
Рассмотрим случай, когда l1|| l2 (рис. 1).
Четырёхугольник А1В1А2В2 - параллелограмм по определению, так как А1В1 || А2В2 по условию теоремы, А1А2 || В1В2 как отрезки, лежащие на параллельных прямых l1 и l2. В параллелограмме противолежащие стороны равны, поэтому А1А2 = В1В2. Аналогично доказывается, что А2А3 = В2В3, А3А4 = В3В4 ; ... . А так как А1А2 = А2А3 = АА4 = ..., то В1В2 = В2В3 = В3В4 = ... .
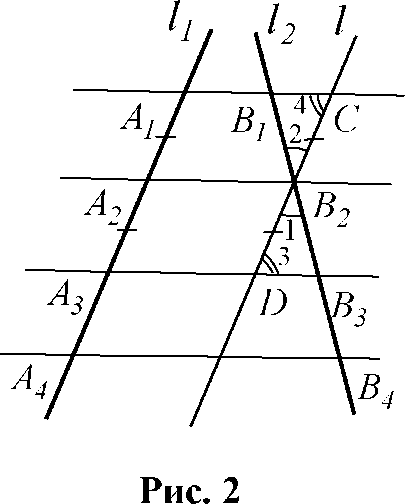
Рассмотрим случай, когда l1 Л l2 (рис. 2).
Через точку В2 проведём прямую l || l1, l П А1В1 = С, l П А3В3 = D.
Так как А1А2 = А2А3, то СВ2 = B2D по пункту I. Рассмотрим получившиеся D В2В1С и D В2В^\ а) СВ2 = В2D по доказанному выше; б) ^ 1 = Z2 как вертикальные углы; в) ^ 3 = Z 4 как накрест лежащие углы, образованные при пересечении параллельных прямых А1В1 и А3В3 секущей l.
Следовательно, D В2В1С = D В2В3D по II признаку равенства треугольников (по стороне и прилежащим к ней углам).
В равных треугольниках соответствующие элементы равны, поэтому В,В2 = В2В3. Аналогично доказывается, что В2В3 = В3В4.
Итак, если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Ч.т.д.
Вопрос № 2 Осевая симметрия. Определение, примеры
Если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя.
Примером отображения плоскости на себя является осевая симметрия.
Две точки А и Ai называются симметричными относительно прямой а,
если эта прямая проходит через середину A отрезка АА1 и перпендикулярна к нему.
Построение
а, А £ а;
АО 1 а; ОА П а = О;
ОА1 = ОА, ОА1 с ОА;
А1 - искомая.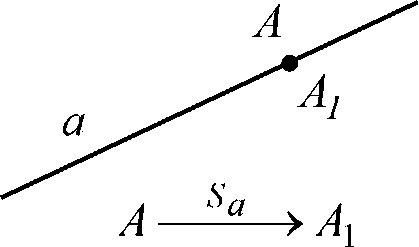
Пусть прямая а - ось симметрии.
Возьмем произвольную точку А, не лежащую на прямой а, и построим симметричную ей точку А1 относительно прямой а.
Для этого проведем перпендикуляр АО к прямой а и отложим на прямой АО от точки О отрезок ОА1 = АО.
Точка А1 - искомая.
Если точка А лежит на прямой а, то симметричная с ней точка А1 совпадает с точкой А.
Каждая точка прямой а считается симметричной самой себе.
Рис. 2
Рис.
1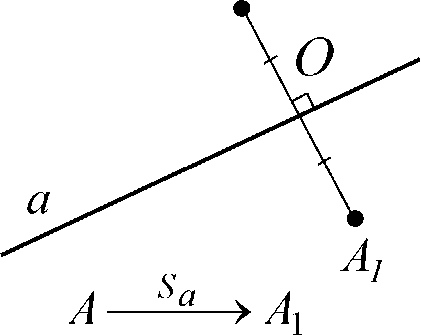
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры. Говорят, что «фигура обладает осевой симметрией».
