Лабораторная работа №5. Решение задачи линейного программирования ее графическая интерпретация и обобщенная транспортная задача

Задания

1. Решить задачи в соответствии с номером варианта. Варианты заданий по частям 1 и 2 приведены в таблице:

Таблица 1. Варианты заданий

Последняя цифра номера зачетки	Часть 1	Часть 2
		Номер задачи	Размер исходного массива
	Задача 1	Задача 5	5 x 4
	Задача 2	Задача 6	4 x 5
	Задача 3	Задача 7	7 x 6
	Задача 4	Задача 5	5 x 7
	Задача 1	Задача 6	5 x 8
	Задача 2	Задача 7	5 x 6
	Задача 3	Задача 5	6 x 7
	Задача 4	Задача 6	6 x 4
	Задача 1	Задача 7	6 x 5
	Задача 2	Задача 5	6 x 6

2. Для части 1 выполнить графическое изображение многоугольника ограничений на плоскости. Построить график целевой функции, проходящий через точку оптимального решения.

3. На листе 2 рабочей книги Excel решить задачу части 2. . Установить размеры массива исходных данных в соответствии с вариантом, пересчитать результат. Изменить исходные данные, пересчитать результат

Задача 1

Для осуществления буксирно-баржевых перевозок на двух линиях А и В портовый флот располагает определенным числом барж четырех типов. По условиям эксплуатации буксирный воз для каждой линии должен состоять из определенного набора барж разных типов.

Требуется распределить имеющиеся баржи по линиям А и В так, чтобы общая грузоподъемность возов была наибольшей. Исходные данные указаны в таблице.

Таблица 2. Исходные данные

Тип баржи	Грузоподъемность баржи	Состав буксирного воза		Количество имеющихся барж
		Линия А	Линия В
I	300	2	2	20
II	500	1	2	14
III	600	4	0	32
IV	800	0	4	24

Указание: Из условия задачи следует, что грузоподъемность одного буксирного воза на линии А составляет 2300+1500+2600+0800=3600 т., а на линии В она равна 4800 т (вычислить с помощью =СУММПРОИЗВ()). Если запланировать x₁ на линию А и x₂ возов на линию В, то добьемся общей грузоподъемности

Z=3600 x₁ + 4800 x₂ т.

Это – целевая функция, которую нужно максимизировать.

Имеем ограничения по числу барж каждого типа, их можно записать в виде неравенств:

2x₁+2x₂≤20

x₁+2x₂≤14

4x₁+0x₂≤32

0x₁+4x₂≤24

Кроме того, очевидно, что x₁≥0, x₂≥0.

Задача 2

Автосборочный цех, выпускающий как легковые, так и грузовые автомобили, имеет в своем составе четыре цеха: кузнечно-прессовый, цех двигателей, сборочный легковых машин и сборочный грузовых машин, производительности которых (за месяц) указаны в таблице. Прибыль предприятия (в ден. ед.) от реализации одной грузовой машины – 250n; и одной легковой – 300n.

Таблица 3. Исходные данные

Цех	Месячный выпуск машин, тыс.штук
	Грузовых	Легковых
Кузнечно-прессовый	53,0	32,0
Двигателей	61,6	33,0
Сборочный грузовых машин	18,0	-
Сборочный легковых машин	-	26,0

Требуется составить месячный план выпуска легковых и грузовых машин, обеспечивающий достижение максимальной прибыли.

Указание: Если планировать месячный выпуск x₁ грузовых и x₂ легковых машин, то предприятие получит прибыль

Z=250 x₁ + 300 x₂.

Это – целевая функция, которую нужно максимизировать. Ограниченные производственные мощности цехов приводят к неравенствам:

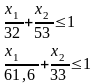
Первое неравенство получено из таких соображений. Если кузнечно-прессовый цех выпускает x₂ легковых машин в месяц, то он на это затрачивает такую долю своей месячной производительности, которая выражается дробью x₂/32. Кроме того, цех работает на выпуск x₁ грузовых машин и затрачивает на это еще такую долю своей месячной производительности, которая выражается дробью x₁/53; сумма этих долей, очевидно, не превышает 1. Из тех же соображений составлено второе неравенство. Третье и четвертое неравенства непосредственно следуют из данных о производительности сборочных цехов.

К этим неравенствам, конечно, надо присоединить условие неотрицательности параметров управления: x₁≥0, x₂≥0.