
- •Математическая статистика. Вариационные ряды и их характеристики.
- •Основные понятия теории оценок
- •Неравенство Чепмена – Роббинса.
- •Неравенство информации.
- •Достаточные статистики.
- •Методы оценки неизвестных параметров. Метод моментов.
- •Метод максимального правдоподобия.
- •Оценка параметров нормального распределения методом максимального правдоподобия и свойства данных оценок.
- •Свойства оценок нормального распределения:
- •Основные статистические распределения.
- •Интервальные оценки.
- •Основные понятия проверки статических гипотез.
- •Подход Неймана - Пирсона к выбору решающей функции .
- •Критерии для проверки гипотезы о виде функции распределения.
- •Критерий согласия Колмогорова. Критерий Колмогорова – Смирнова. Критерий согласия Колмогорова:
- •Критерий согласия Колмогорова - Смирнова:
- •Проверка гипотезы о нормальном распределении выборочных значений по критерию Пирсона.
- •Проверка гипотезы о распределении выборочных значений по закону Пуассона.
- •Задача регрессионного анализа.
- •Определение оценок коэффициентов регрессии по данным пассивного эксперимента.
- •Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ.
- •Однофакторный дисперсионный анализ
Критерий согласия Колмогорова. Критерий Колмогорова – Смирнова. Критерий согласия Колмогорова:
Пусть имеем:
![]() ,
,
где
- некоторая заданная функция распределения.
,
,
где
- некоторая заданная функция распределения.
![]() ,
где
,
где
![]() - эмпирическая функция распределения
по выборке
.
- эмпирическая функция распределения
по выборке
.
Распределение величины
![]() определил Колмогоров:
определил Колмогоров:
![]() ,
где
,
где
![]() - функция Колмогорова.
- функция Колмогорова.
Задавая уровень значимости
![]() из соотношения:
из соотношения:
![]() можно найти критерий значения распределения
Колмогорова (по таблице).
можно найти критерий значения распределения
Колмогорова (по таблице).
Т. о. применяя критерии Колмогорова:
![]() и сравнивают его с табличным значением:
и сравнивают его с табличным значением:
![]() ,
при заданном
,
при заданном
![]() ,
то говорят, что табличные значения
распределены по закону
,
то говорят, что табличные значения
распределены по закону
![]() .
.
Критерий согласия Колмогорова - Смирнова:
Со случайной величиной
проводят 2-е серии опытов. В результате
получим 2 выборки:
![]() и
и
![]() (объём).
(объём).
Пусть
![]() и
и
![]() функция распределения СВ
в 1-ой и 2-ой серии соответственно.
функция распределения СВ
в 1-ой и 2-ой серии соответственно.
Будем рассматривать следующие задачи:
Требуется проверить теорию:
![]() .
.
Пусть
![]() и
и
![]() - выборочные эмпирические функции
распределения в 1-ом и 2-ом выборочном
соответствии. Критерии Колмогорова –
Смирнова заключается в следующем:
- выборочные эмпирические функции
распределения в 1-ом и 2-ом выборочном
соответствии. Критерии Колмогорова –
Смирнова заключается в следующем:
![]() .
Если
.
Если
![]() ,
то
принимается, в противном случаи
принимается гипотеза
.
,
то
принимается, в противном случаи
принимается гипотеза
.
Критическое значение
![]() при заданном значении
определяется как и в случаи критерия
Колмогорова.
при заданном значении
определяется как и в случаи критерия
Колмогорова.
Проверка гипотезы о нормальном распределении выборочных значений по критерию Пирсона.
Пусть задана выборка
![]() ,
причём:
,
причём:
![]() ,
,
![]() - равноотстоящие.
- равноотстоящие.
Вычислим выборочное среднее и выборочное среднее квадратичное отклонения:
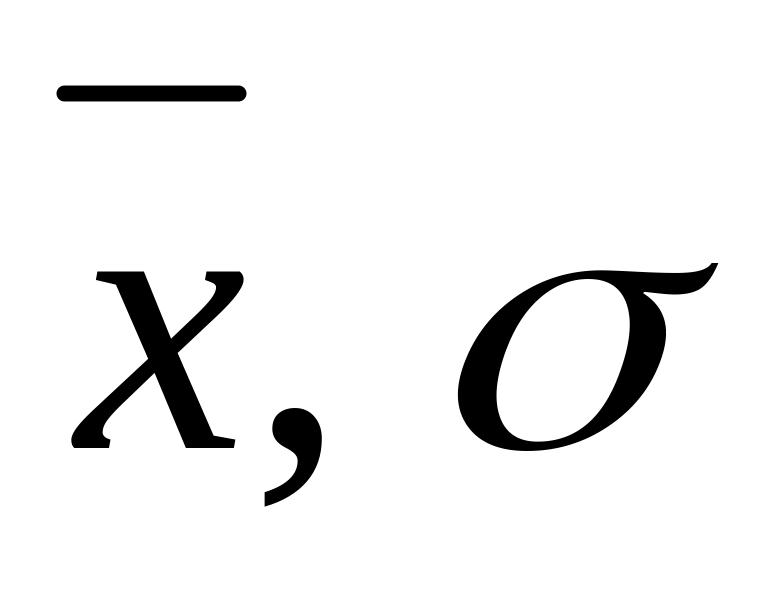 :
:
 .
.
Вычислим теоретические частоты:
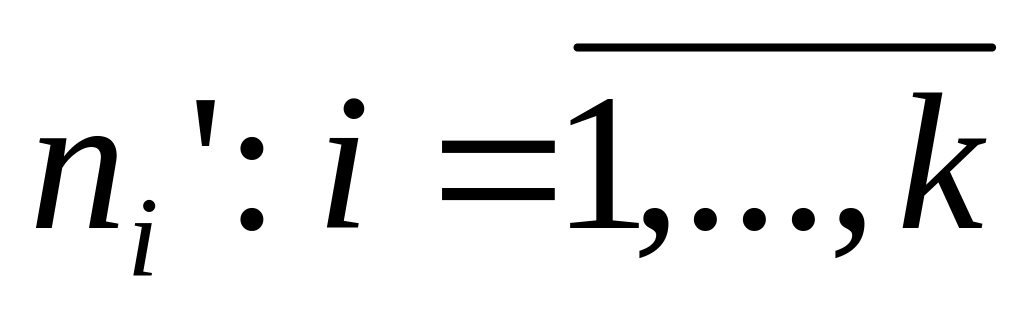 ,
,
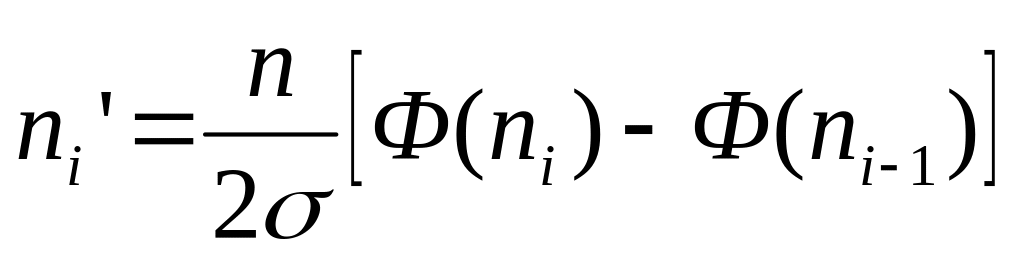 ,
,
 - функция Лапласа.
- функция Лапласа.
Сравниваем эмпирические частоты
 с теоретическими
с теоретическими
 с помощью критерия
с помощью критерия
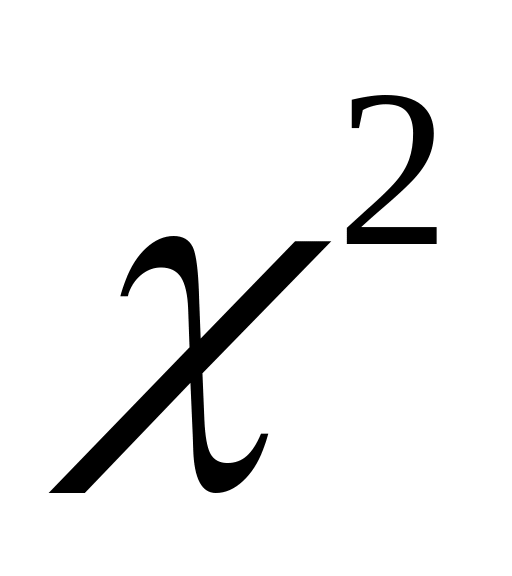 :
,
:
,
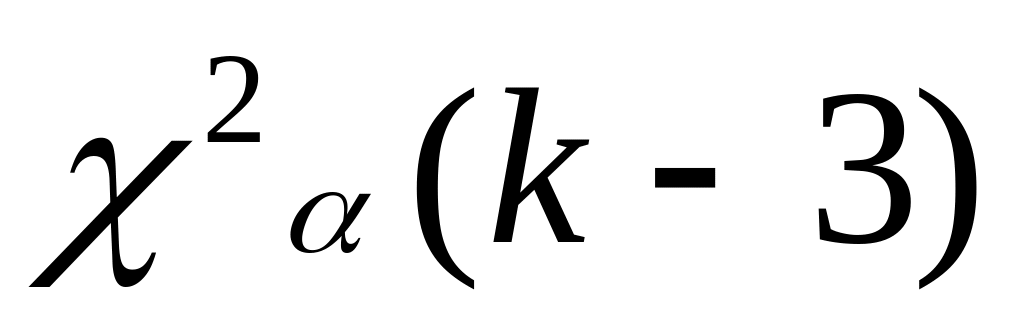 .
Если
.
Если
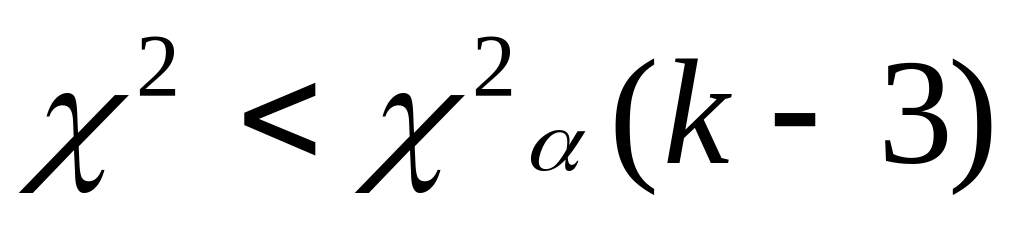 - говорим, что выборочные значения
нормально распределены.
- говорим, что выборочные значения
нормально распределены.
Проверка гипотезы о распределении выборочных значений по закону Пуассона.
Пусть задана выборка
,
причём:
,
![]() - равноотстоящие.
- равноотстоящие.
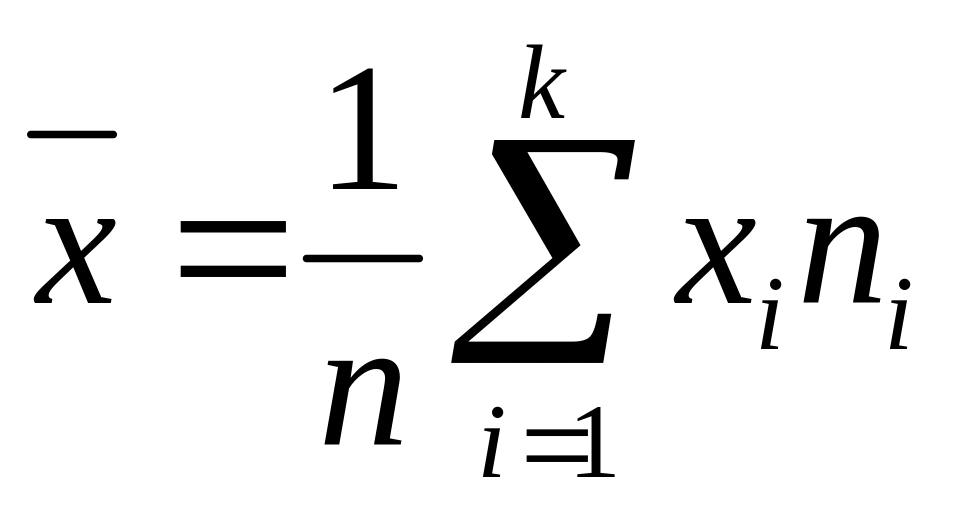
В качестве оценки параметра
 .
.Найти предполагаемый закон Пуассона:
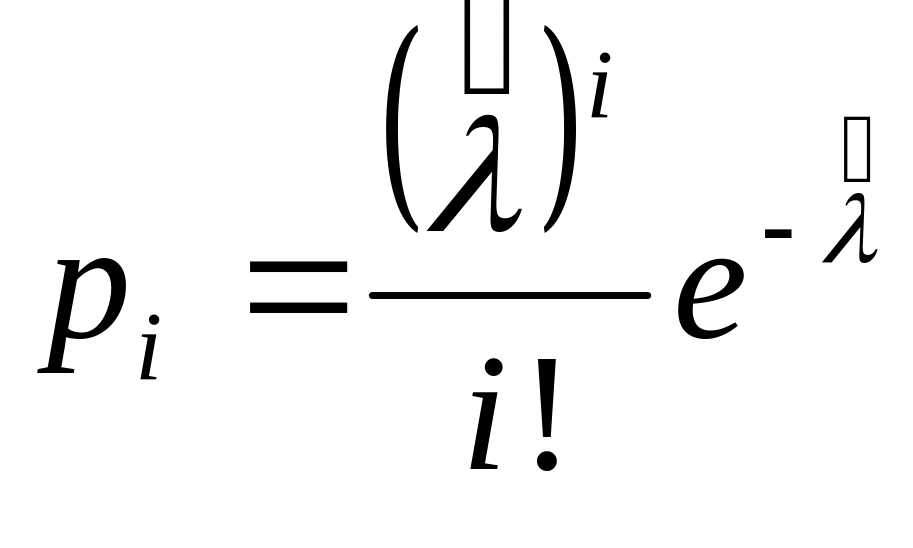 ,
где
,
где
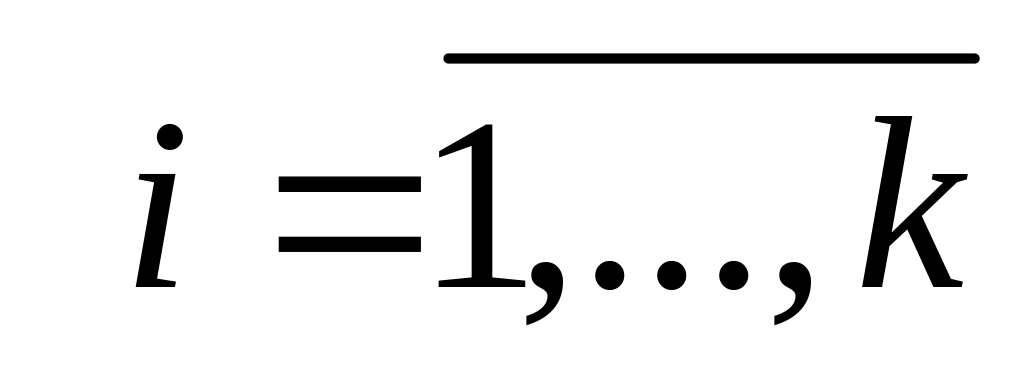 .
.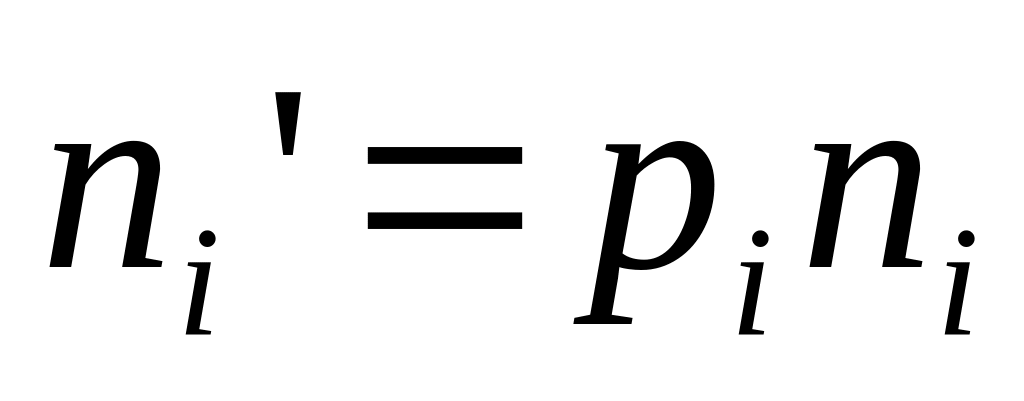 ,
где
(теоретические частоты)
,
где
(теоретические частоты)
, но
 .
.
Если
![]() ,
то выборочное значение распределено
по закону Пирсона.
,
то выборочное значение распределено
по закону Пирсона.
Задача регрессионного анализа.
Рассмотрим следующую задачу:
Есть
![]() независимы переменных и зависящая от
них переменная
независимы переменных и зависящая от
них переменная
![]() .
Сами переменные могут быть случайными
и при желании можем задать их значения.
На величину
также влияют другие неподдающиеся
точному фактору, а это значит, что
величина
носит случайный характер.
.
Сами переменные могут быть случайными
и при желании можем задать их значения.
На величину
также влияют другие неподдающиеся
точному фактору, а это значит, что
величина
носит случайный характер.
Нас будет интересовать методы
экспериментального определения влияния
переменных
![]() на
,
а именно: определить по данным эксперимента
вид зависимости:
на
,
а именно: определить по данным эксперимента
вид зависимости:
![]() .
.
Задача регрессионного анализа состоит
от экспериментально определённых
коэффициентов регрессии вида:
![]() путём наблюдения за характером изменений
входных переменных
и выходного
,
служат методы активного и пассивного
эксперимента.
путём наблюдения за характером изменений
входных переменных
и выходного
,
служат методы активного и пассивного
эксперимента.
Пассивный эксперимент основан на регистрации контроля параметра в процессе нормальной работы объекта без внесений преднамеренных возмущений.
Активный эксперимент основан на использовании искомого возмущения вводимых в объект по заранее спланированной программе. При активном эксперименте ведение искомых возмущений позволяет быстро и целенаправленно вскрывать нужные зависимости между параметрами, но введение искомых возмущений может привести к нарушению нормального хода технологий.
При организованном числе экспериментов
невозможно точно найти значение
![]() .
Поэтому находят оценки этих коэффициентов
.
Поэтому находят оценки этих коэффициентов
![]() ,
,
![]() определяют оценку математического
ожидания истинной функции
определяют оценку математического
ожидания истинной функции
![]() .
.
