
- •Математическая статистика. Вариационные ряды и их характеристики.
- •Основные понятия теории оценок
- •Неравенство Чепмена – Роббинса.
- •Неравенство информации.
- •Достаточные статистики.
- •Методы оценки неизвестных параметров. Метод моментов.
- •Метод максимального правдоподобия.
- •Оценка параметров нормального распределения методом максимального правдоподобия и свойства данных оценок.
- •Свойства оценок нормального распределения:
- •Основные статистические распределения.
- •Интервальные оценки.
- •Основные понятия проверки статических гипотез.
- •Подход Неймана - Пирсона к выбору решающей функции .
- •Критерии для проверки гипотезы о виде функции распределения.
- •Критерий согласия Колмогорова. Критерий Колмогорова – Смирнова. Критерий согласия Колмогорова:
- •Критерий согласия Колмогорова - Смирнова:
- •Проверка гипотезы о нормальном распределении выборочных значений по критерию Пирсона.
- •Проверка гипотезы о распределении выборочных значений по закону Пуассона.
- •Задача регрессионного анализа.
- •Определение оценок коэффициентов регрессии по данным пассивного эксперимента.
- •Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ.
- •Однофакторный дисперсионный анализ
Методы оценки неизвестных параметров. Метод моментов.
Пусть есть вектор неизвестных параметров:
![]() ,
- СВ с плотностью распределения
,
- СВ с плотностью распределения
![]() ,
по выборке
,
по выборке
![]() .
.
![]() ,
тогда начальный момент k-го
порядка СВ
может быть вычислен по формуле:
,
тогда начальный момент k-го
порядка СВ
может быть вычислен по формуле:
![]() ,
,
![]() - количество неизвестных параметров.
- количество неизвестных параметров.
По выборке
можно вычислить оценку моментов k-го
порядка по формуле:
![]() .
.
Метод моментов заключается в том, что оценку неизвестных параметров находим из системы уравнений полученной путём приравнивания теоретических моментов к выборочным.
Система имеет вид:
![]() .
Достоинство данного метода является
простота получения оценок, а недостатком
– оценки моментов высших порядков дают
очень большие ошибки, поэтому нужно
использовать моменты не выше 4-го порядка,
т.е. число оценок порядка не должно
превышать 4.
.
Достоинство данного метода является
простота получения оценок, а недостатком
– оценки моментов высших порядков дают
очень большие ошибки, поэтому нужно
использовать моменты не выше 4-го порядка,
т.е. число оценок порядка не должно
превышать 4.
Метод максимального правдоподобия.
Пусть
![]() выборка. Производимые опыты являются
независимыми:
выборка. Производимые опыты являются
независимыми:
![]() ,
где
,
где
![]() неизвестные параметры.
неизвестные параметры.
Определение:
![]() называется функцией правдоподобия.
называется функцией правдоподобия.
Метод максимального правдоподобия заключается в следующем:
В качестве оценки неизвестного параметра
следует брать те значения аргумента,
при котором функция правдоподобия
достигает своего максимума:
![]() .
.
Определение: Оценка получаемая по методу оценки максимального правдоподобия называется оценкой максимального правдоподобия.
Замечание: В целях удобства вместо
функции правдоподобия рассмотрим её
логарифм:
![]() ,
т.к. функция и её логарифм достигают
своего максимума при одном и том же
.
,
т.к. функция и её логарифм достигают
своего максимума при одном и том же
.
Оценка параметров нормального распределения методом максимального правдоподобия и свойства данных оценок.
Пусть есть СВ для которой плотность распределения задаётся формулой:
![]() ,
где
,
где
![]() - неизвестные параметры,
- математическое ожидание,
- неизвестные параметры,
- математическое ожидание,
![]() - дисперсия. Полученная выборка
является реализованная СВ
.
- дисперсия. Полученная выборка
является реализованная СВ
.
Найдём оценки
![]() и
и
![]() неизвестных параметров:
неизвестных параметров:
Запишем функцию правдоподобия:
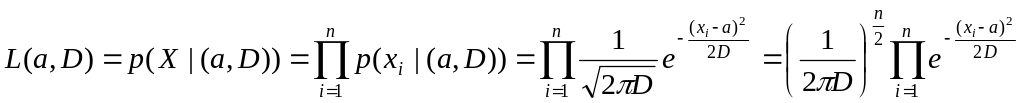 ,
,
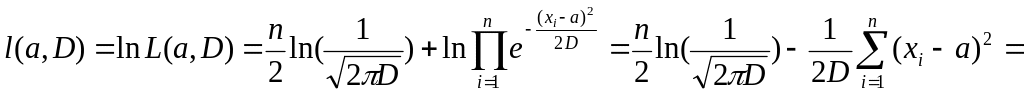
![]() ,
,
![]() .
.
Получим:
![]() ,
,
![]() .
.
Свойства оценок нормального распределения:
1)
![]() ,
т.к. математическое ожидание случайной
величины равно
:
,
т.к. математическое ожидание случайной
величины равно
:
![]() .
.
2)
![]() ,
где
,
где
![]() .
.
Исследуем поведение оценки:
![]()
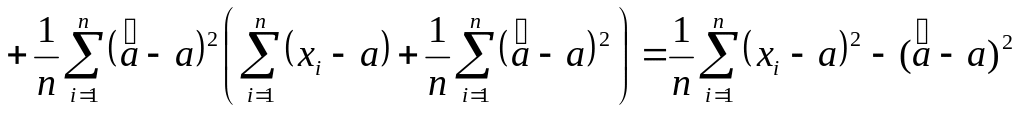 ,
,
![]() ,
,
Упражнение:
![]() - несмещённая оценка параметра
.
- несмещённая оценка параметра
.
Основные статистические распределения.
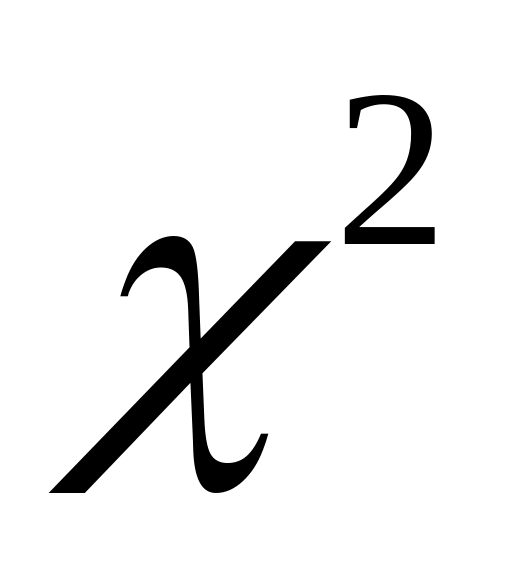 - распределение (распределение
Пирсана). Это распределение имеет
следующий вид:
- распределение (распределение
Пирсана). Это распределение имеет
следующий вид:
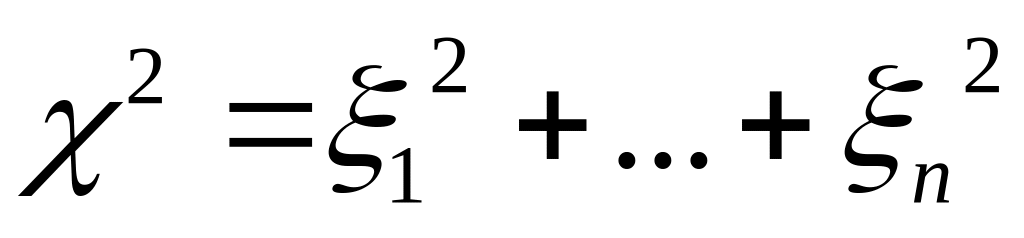 ,
где
,
где
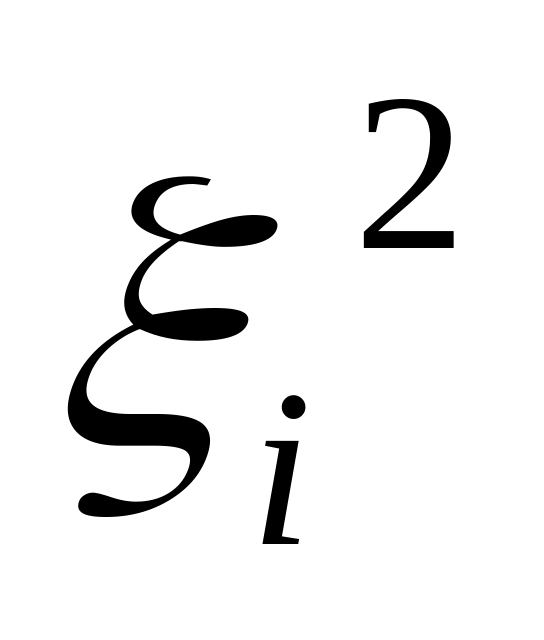 - распределено по нормальному закону
с параметрами
- распределено по нормальному закону
с параметрами
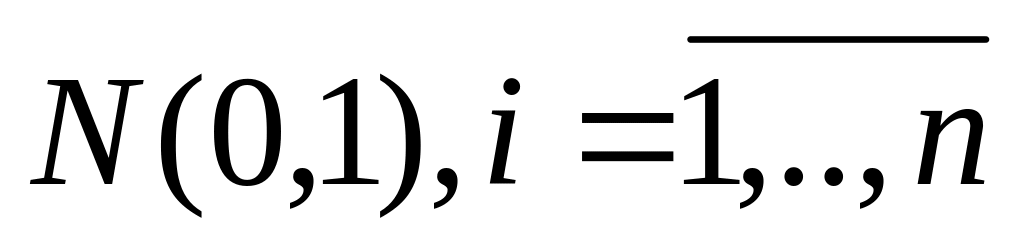 .
Иногда распределении обозначают:
.
Иногда распределении обозначают:
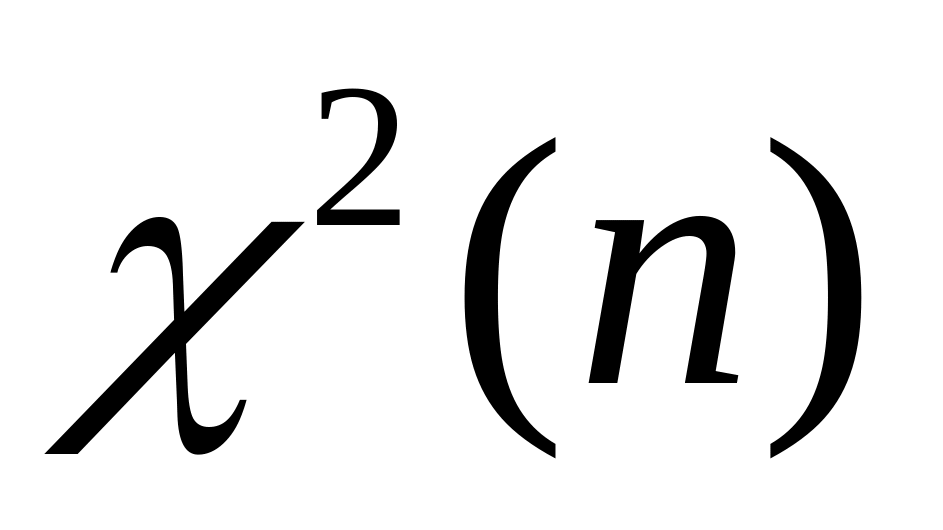 ,
n – число степеней свободы.
,
n – число степеней свободы.
- распределение (Стьюдента). Пусть имеются СВ: и
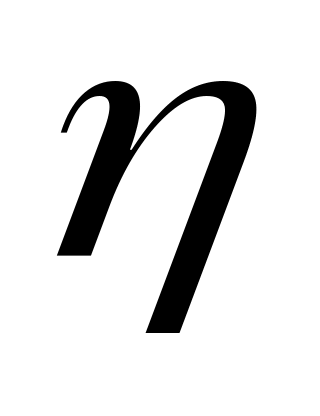 .
Тогда:
.
Тогда:
 ,
,
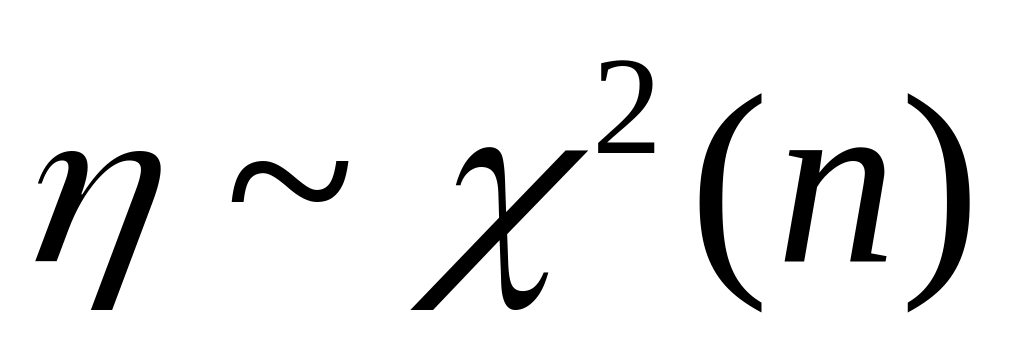 ,
,
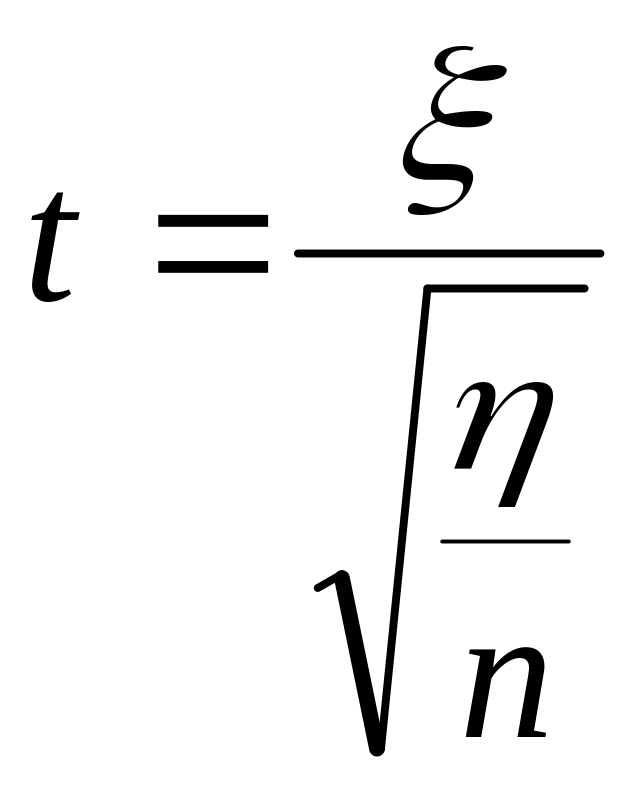 ,
если t-распределение:
,
если t-распределение:
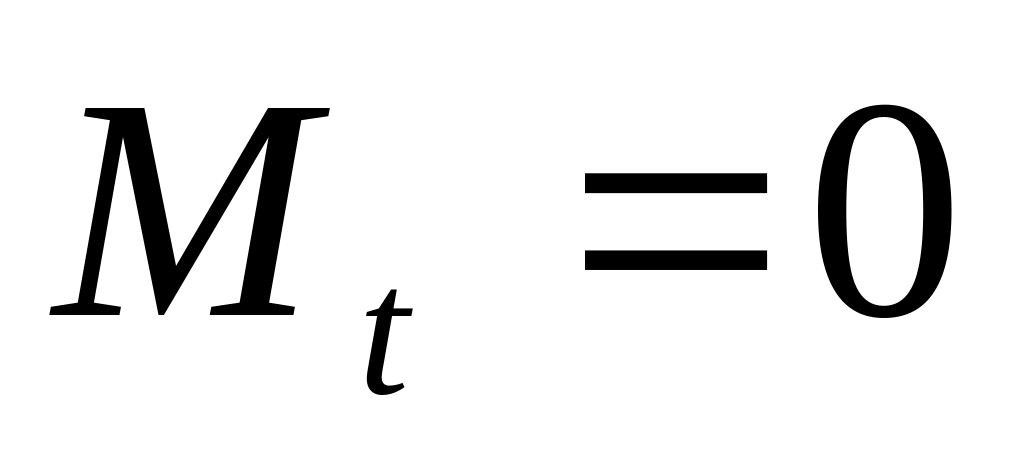 и
и
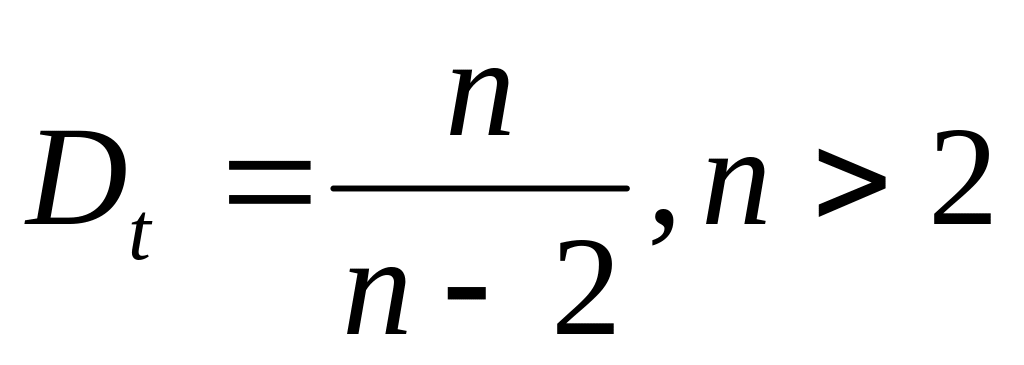 .
.Распределение Спедекора-Фишера – это распределение имеет СВ вида:
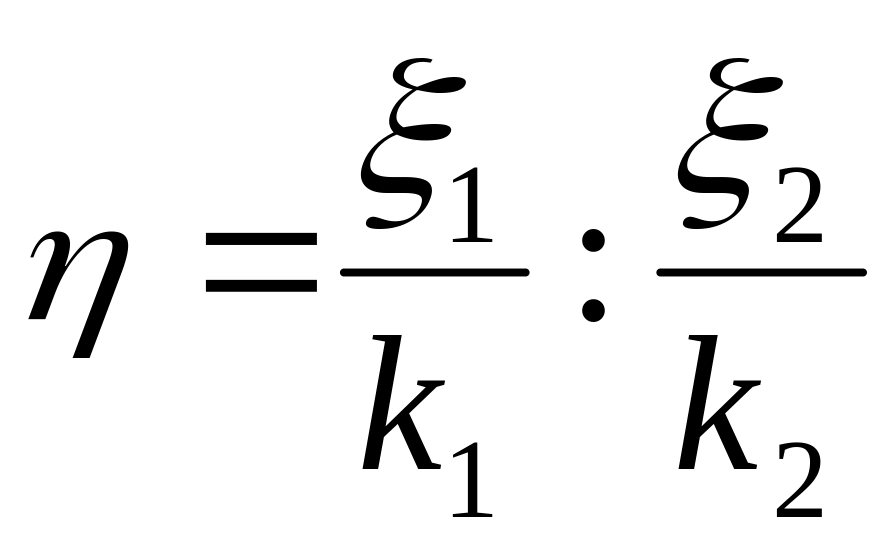 ,
,
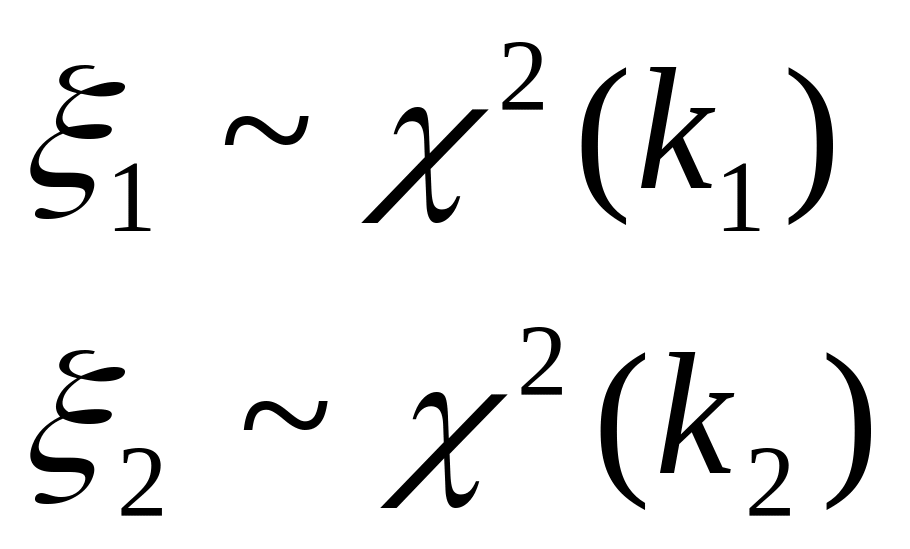 ,
,
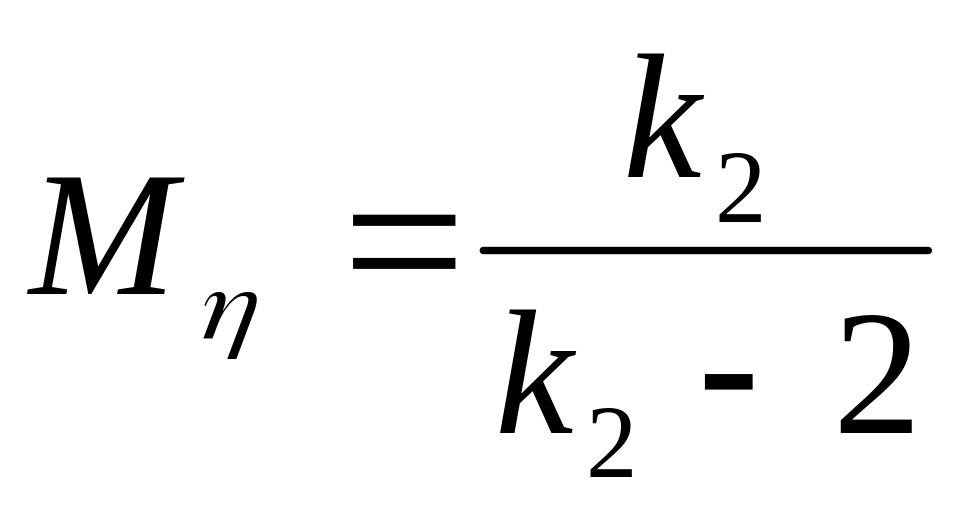 ,
,
 .
.
Интервальные оценки.
Если известен закон распределения оценки или её дисперсия, то можно указать приделы в которых с большой вероятностью находятся неизвестные значения параметра.
Пусть имеется выборка
.
Предположим, что выборочные значения
распределены по закону:
![]() с точностью до
.
с точностью до
.
Предположим, что мы нашли функцию:
![]() и
и
![]() ,
причём
,
причём
![]() ,
,
![]() и
и
![]() .
Величина
.
Величина
![]() называется доверительным уровням.
Обычно
берётся очень маленьким: 0.05, 0.01…
называется доверительным уровням.
Обычно
берётся очень маленьким: 0.05, 0.01…
Вероятность того, что
![]() покроет неизвестный параметр
не зависит от
.
В этом случаи интервал
покроет неизвестный параметр
не зависит от
.
В этом случаи интервал
![]() - доверительный интервал для неизвестного
параметра соответствующей доверительной
вероятности
- доверительный интервал для неизвестного
параметра соответствующей доверительной
вероятности
![]() .
.
Пример:
Пусть имеется выборка
.
Предположим, выборка распределена по
нормальному закону:
![]() ,
где
- неизвестно, а
,
где
- неизвестно, а
![]() - известно.
- известно.
Найдём доверительный интервал для
параметра
.
Известно, что
![]() (по
центральной предельной теореме)
(по
центральной предельной теореме)
![]() ,
тогда величина
,
тогда величина
![]() распределена по закону
распределена по закону
![]() .
Доверительный интервал будем строить
используя следующее соотношение:
.
Доверительный интервал будем строить
используя следующее соотношение:
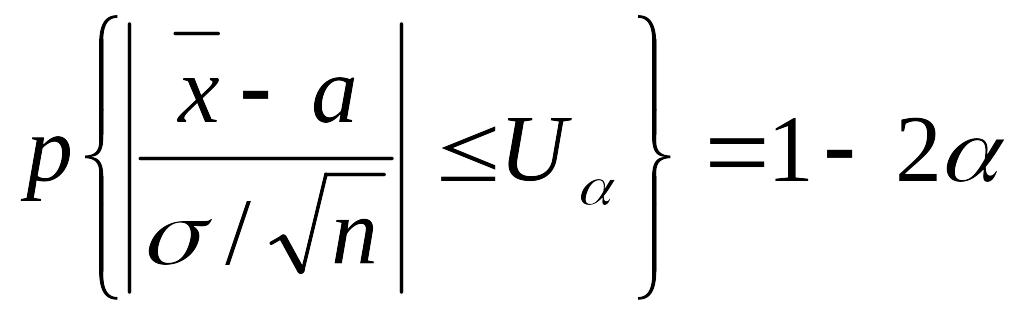 ,
где
,
где
![]() -находится
путём решения уравнения:
-находится
путём решения уравнения:
![]() (по заданному уровню
).
Окончательно имеем:
(по заданному уровню
).
Окончательно имеем:
![]() .
Доверительный интервал имеет вид:
.
Доверительный интервал имеет вид:
![]() .
.
