13. Общая задача нелинейного программирования (знп). Выпуклость области допустимых решений.

Найти (1) при (2) и (3)

Считается что хоть одна из функций в (1),(2),(3) - нелинейная. Считая, что , , определенные на открытом множестве

Если непрерывны то Х замкнуто и совпадает с

Если по системе ограничений (2), (3) можно сказать, что множество допустимых решений выпукло и функция на этом множестве выпукла то задача минимизации имеет решение, причем каждая точка локального минимума является точкой глобального минимума функции цели.

Теорема:

Если выпуклы в то множество допустимых решений тоже является выпуклым.

Доказательство:

Если или то все катит (очевидно).

Если выпукло имеем

Если область допустимых решений определяется только ограничениями вида (3) и каждая функция выпукла в то область допустимых решений также выпукла.

В том случае если присутствуют ограничения типа (2) то доказательство выпуклости усложняется. Однако когда линейны то в этом случае пространство разбивается на подпространства с помощью гиперплоскостей.

В этом случае экстремум функции цели будет принадлежать области пересечений ограничений типа (2) и расположенных внутри выпуклой области определенной ограничениями типа (3).

Во многих случаях общую задачу нелинейного программирования можно свести к задаче с ограничениями типа равенств записав (3) в виде

14. Алгоритм решения знп на выпуклом множестве.

Общая задача формулируется так:

f(x)→min; g_i(x)=0 (i=1,m) φ_k(x)≤0;(k=1,s)

Во многих случаях общую ЗНП можна свести к задаче с ограничениями типа равенств записав φ_k(x)≤0;(k=1,s) в виде φ_к(х)+Z²_k=0.

Стандартная методика.

f(x₁,x₂)≤0; φ₁(x₁,x₂) ≤0; φ₂(x₁,x₂) ≤0; φ₃(x₁,x₂) ≤0;

Пусть все это выпукло.

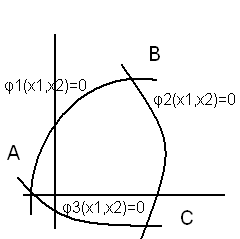
1. Ищем стационарные точки (grad f(x)=0), принадлежащие U.

2. Решается 3 задачи поиска экстремума функции на отрезках AB, BC, AC.

3. Определяем наличие минимума в угловых точках A, B, C.

4. В найденных точках стационарности функции цели и в угловых точках A, B, C вычисляем значения функции f(x) и среди них находятся наименьшие

15. Обобщенная функция Лагранжа для знп со смешанными ограничениями. Теорема о существовании решения (первая теорема Куна-Таккера).

Рассмотрим задачу нахождения минимума функции цели при смешанных ограничениях.

(*)(этих три строки)

f(x)→min;

g_i(x)=0 (i=1,m)

φ_k(x)≤0;(k=1,5)

Условия регулярности (Слейтера) или условиями смягчающей жесткости называется запись выражения φ_k(x)≤0;(k=1,5) в виде μ_kφ_k(x)=0, причем μ_k – некоторые любые числа и (положительному ортанту). Т.е. μ_k≥0. Очевидно что μ_kφ_k(x)=0 в точках на границе области т.к φ_k(x)=0. А в точках внутри области φ_k(x)≤0; то μ_k=0. В этом случае для (*) можно построить обобщенную функцию Лагранжа в виде:

.(**)

Теорема о существовании решения (первая теорема Куна-Таккера).

Если точка х* является точкой локального минимума функции f(x) в области допустимых решений U(x) и g_i(x),φ_i(x)- непрерывны и дифиринцируемые в окрестности точки х*, то существуют такие одновременно не равные нулю, что для функции Лагранжа (**) выполняются необходимые условия существования экстремума ( ) и условие дополнительной нежесткости μ_kφ_k(x)=0.