9. Минимизация на заданном множестве. Теорема о существовании решения.

, тут f(x) – функция многих переменных.

Если U - компактное, тогда существует точка , в котором н/п ф-я f(x) достигает своего наименьшего значения.

Теорема. Если ф-я f(x) н/п в замкнутом множестве U, и для некоторого выполняется, что на подмножестве , непустом и ограниченом, то задача (1), (2) имеет решения.

Доказательство. Т.к. м-во Х задается нестрогим неравенством, , то это множество замкнутое. Покажем это: Пусть - некоторая предельная точка м-ва Х, то всегда существ. некоторая ее -окрестность, которая содержит точки из Х. Тогда если взять , найдутся точки м-ва Х, для которых => сущест. - окрестность в пересечении с м-вом U дающая непустое м-во. Можем найти -окрестности и .

Тогда можем получить , что . Тоесть м-во Х буд. замкнутым и ф-ция будет определена и на границе. Если м-во U выпукло, то минимум единственный.

10. Допустимое направление. Конус допустимых направлений. Теорема о достаточном условии существования минимума дифференцируемой функции.

Если , то говоримм, что в х существует допустимое направление вдоль в-ра , если сущ. , что также пренадлежит U.

Совокупность всех возможных направлений в т. х назыв. конусом возможных направлений. Конус учитывает направление возрастания, убывания и стационарности, если точка внутри области. Область допустимых направлений не сущ. для невыпуклых облавтей.

Если U –выпуклая, то тогда выбирая и выбирая , то , и задается совокупностью всех направлений, если еще использовать и базис.

Теорема. Пусть f(x) –диференц. в некоторой точке . Если x* есть точкой наименьшего значения f(x) в области U, то (3), где - любой вектор области допустимых направлений.

Если x* - точка лок.мин f(x) –то никакое из ее направлений не является направлением убывания.

11. Минимизация при ограничениях типа равенств. Функция Логранджа.

Пусть область U задается равенствами

Будем считать что f(x),g(x) дифер. в n-мерном пространстве и Якобиан для g(x) имеет ранг m.

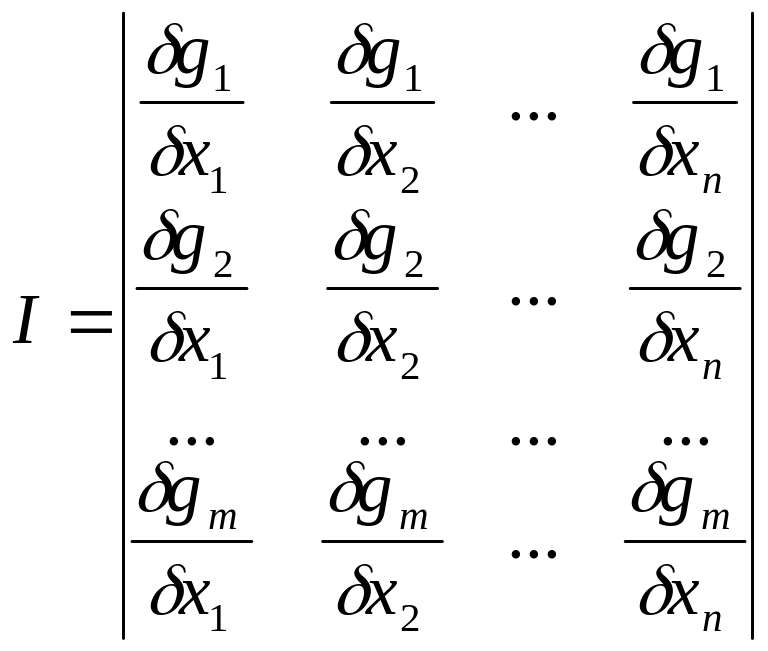
Подставим найденые переменные в ф-цию цели поелчим задачу минимизации ф-ции.В общем случае решить задачу для m неизвестных трудно решить.

Метод множетелей Логранджа.

Для решения (1) и (2) строят ф-цию: , где -множетель Логранджа, которые будут при . Тогда минимизация эквивалентна миним. (1) при условии (2). Необходимое условие минимума .

Решая эту систему получаем точки стационарности ф-и Логранджа.

Теорема. Пусть f(x) и g(x) – диферен. в . Тогда если точка x* является решением этой задачи и Якобиан не равен 0, то сушествует вектор , такой что причем

12. Обобщенная функция Лагранжа. Теорема о существовании стационарной точки функции Лагранжа.

Пусть имеем задачу

Найти (1) при (2)

Точки экстремума (1), (2):

1. Точки стационарности

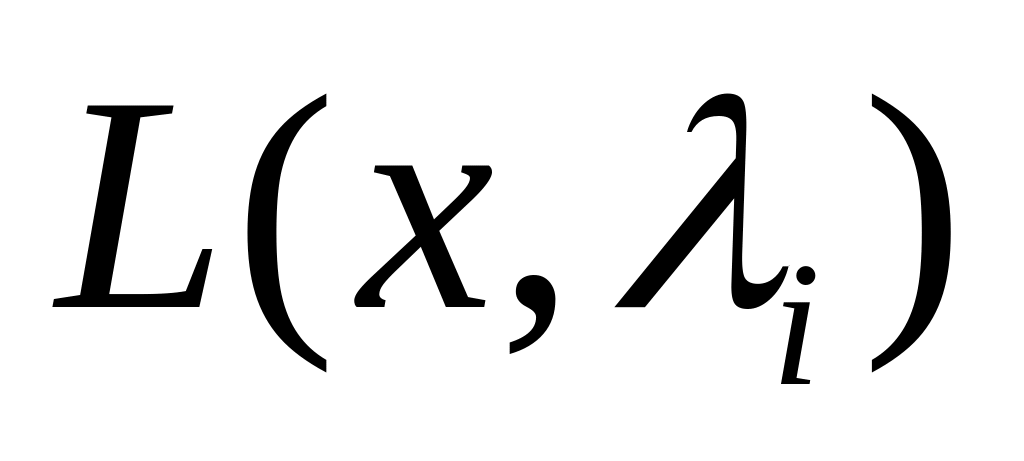
2. Точки, где якобиан =0

3. Точки, в которых хоть одна функция 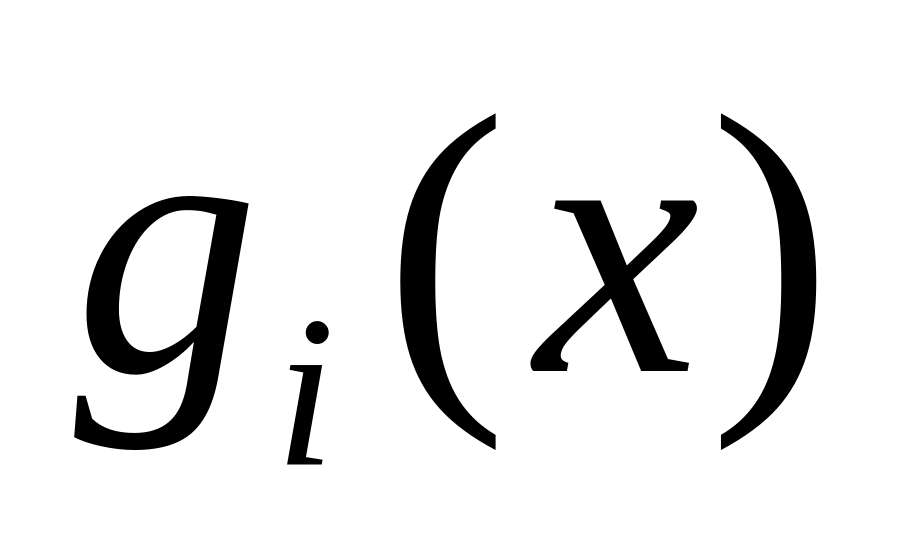не дифференцируема или имеет разрывную частную производную

Когда нужно найти точки при 2) или 3) то для повышения качества вводят дополнительный параметр Лангранжа и строят обобщенную функцию Лангранжа

(6)

Теорема:

Если точка - точка условного экстремума функции (1) при условиях (2) причем - непрерывна в некоторой окрестности и дифференцируемы в этой окрестности то

причем не все лямбды одновременно равны нулю. Для функции (6) точка есть стационарной, т.е.

Если линейно независимы и последнее равенство теоремы будет выполнятся когда хоть одно

Но положив запишим

получим возможность определить вектор лямбд с точность до нескольких множителей