1. Релаксационная последовательность, Оценка сходимости.
Последовательность
точек
называется релаксационной, если для
каждой точки
выполняется
.
Введем
.
Последовательность
- сходящаяся, и
=0
тогда когда
.
Последовательность
положительная, но при переходе через
х*
- отрицательная.
2. Релаксационная последовательность, Оценка сходимости для выпуклых дифференцируемых функций.
Теорема.
Пусть минимизируемая ф-я
выпукла и дифференцируема на
,
и последовательность
есть
релаксационной. Тогда, если
,
то справедлива следующая лемма:
Лемма
Если для элементов
последовательности
справедливо
,
то справедлива оценка вид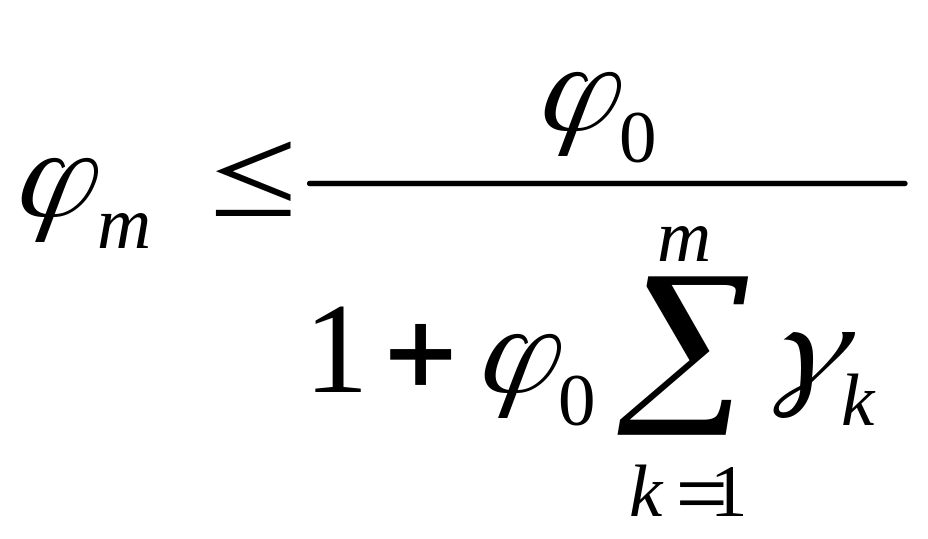а:
.
(А)
Доказательство:
Разделим
на
.
Получим:
.
Просуммировав это, получим:
.
Решая последнее неравенство и получим
нашу оценку (А)
3. Методы спуска. Оценка спуска для выпуклых дифференцируемых в Rn функциях.
Пусть существует
точка
,
в которой целевая функция f(x) достигает
минимума. Процедуру поиска этой точки
в методах спуска обычно описывают (после
выбора начальной точки х0) рекуррентным
соотношением
.
(А). где
— единичный вектор, определяющий
направление спуска на к итерации, а
— длина шага спуска, т.е. расстояние в
этом направлении, отделяющее точку
от новой точки
.
Методы спуска различаются способами
выбора направления и шага спуска.
<!--
Если на к-й итерации
выбран вектор
,
то один из способов выбора значения
базируется на требовании, чтобы
выполнялось неравенство:
(В), где
.
Отметим, что выбор значения
в соответствии с последним неравенством
обеспечивает что последовательность
,
построенная в соответствии (А), будет
релаксационной.
При
неравенство (В) переходит в равенство,
а значение
соответствует минимальному значению
f(x) на множестве
.
В этом случае для нахождения
надо решить задачу одномерной оптимизации.
-->
Лемма.
Если все элементы последовательности
подпадают под условие
то в этом случае справедлива оценка
(А).
Теорема.
Если ф-я
выпукла и дифференцируема в некотором
множестве
,
а
-релаксационная
последовательность, то при
, где
- диаметр множества
,
выполняется оценка (А) ил вышеприведенной
леммы.
Теорема.
Для сильно выпуклой функции дифференцируемой
в
при
,
где
-параметр
сильной выпуклости,
.
Последнее неравенство задает сходимость
по точкам релаксационной последовательности.
4. Исчерпывающий спуск при безусловной минимизации в Rn.
Пусть целевая функция f(x) ограничена снизу и непрерывно дифференцируема в . Предположим, что существует точка ,в которой эта функция достигает локального минимума. Рассмотрим некоторые особенности применения метода градиентного спуска для поиска этой точки.
В этом методе
элементы релаксационной последовательности
удовлетворяют рекуррентному соотношению
вида
.
Тут
- шаг спуска, а направление спуска задано
единичным вектором
,
сонаправленным антиградиенту, т.е.
.
Пусть
,
где
-шаг
спуска на каждой итерации пропорционален
длине вектора антиградиента в точке
.
Если функция f(x) непрерывно дифференцируема
в
,
то скалярное произведение
является непрерывной
функцией. Ясно, что функция f(x) убывает
в
направлении
антиградиента до тех пор, пока это
произведение остается отрицательным.
Поэтому один из способов выбора значения
на к-й итерации состоит в том, чтобы
.
Указанный способ называют исчерпывающим спуском