1.4. Динамические характеристики объекта идентификации

На следующем этапе курсовой работы необходимо построить динамические характеристики объекта идентификации. Дифференциальное уравнение исследуемого объекта имеет вид:

;

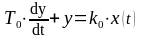Переходная и импульсная функции:

;

.

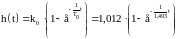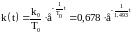По передаточной функции объекта

,

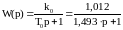подстановкой 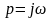определены его частотные характеристики:

;

;

.

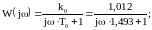
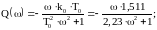
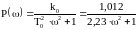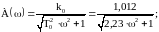
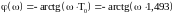Все частотные и временные характеристики представляются соответствующими графиками ( рисунках 1.5, 1.6, 1.7, 1.8, 1.9, 1.10 ).

h(t)

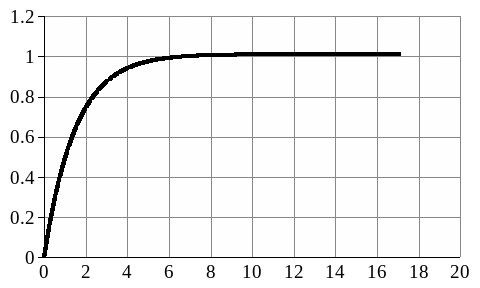
t

Рисунок1.5 - Переходная функция объекта идентификации

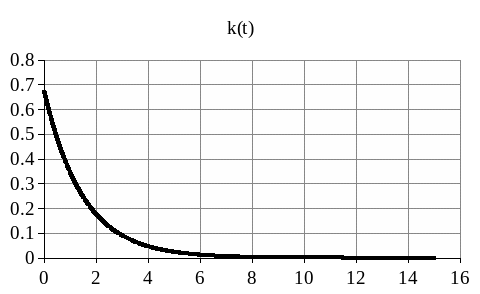
t

Рисунок 1.6 - Импульсная функция объекта идентификации

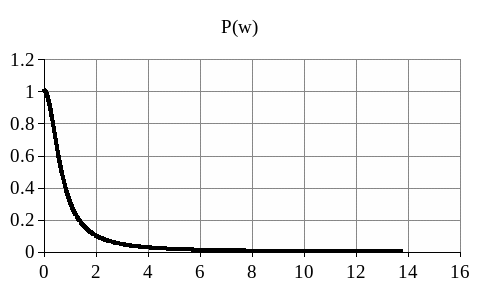
w

Рисунок 1.7 - Вещественная частотная характеристика объекта идентификации

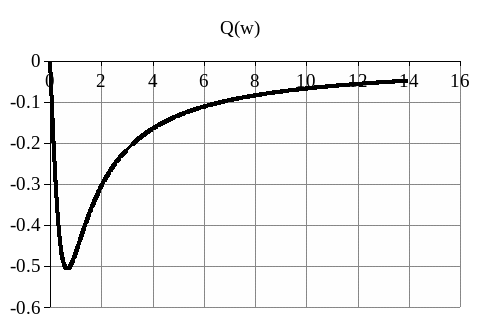
w

Рисунок 1.8 - Мнимая частотная характеристика объекта идентификации

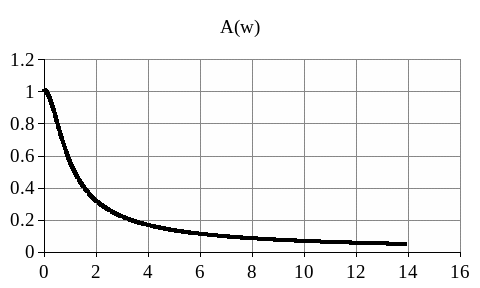
w

Рисунок 1.9 - Амплитудно-частотная характеристика объекта идентификации

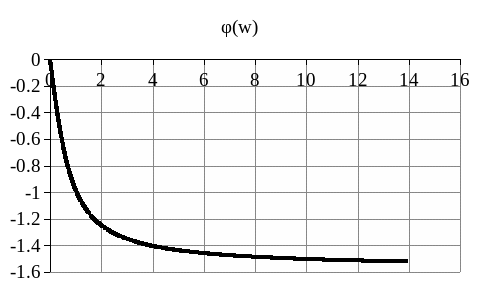
w

Рисунок 1.10 - Фазово-частотная характеристика объекта идентификации

+j

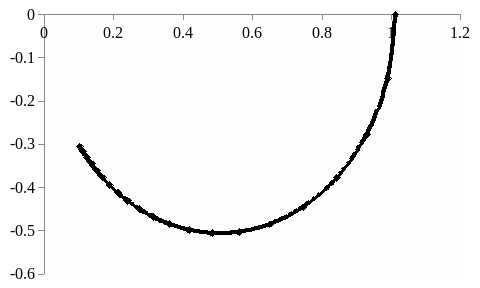
+1

Рисунок 1.11 - Годограф объекта идентификации

2. Оптимизация системы автоматического

РЕГУЛИРОВАНИЯ

2.1. Постановка задачи оптимизации

На рисунке 2.1 представлена структурная схема системы автоматического регулирования. Объект регулирования задан инерционным звеном второго порядка с передаточной функцией

,

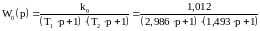где 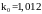– передаточный коэффициент объекта, найденный процедурой идентификации.

Постоянные времен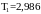и и 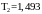рассчитываются:

Т₁ = 2Т₀;

Т₂ = Т₀,

где 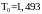– постоянная времени объекта, определенная процедурой идентификации.

Структура регулирующего устройства задана передаточной функцией (изодромный регулятор):

,

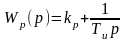где 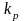– передаточный коэффициент регулятора, 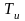– время изодрома.

Структура САР считается заданной. Параметры регулятора и неизвестны и подлежат определению.

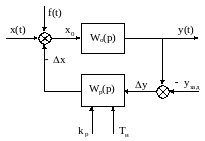
Рисунок 2.1 - Структурная схема САР

На объект управления действуют возмущения f(t), имеющие случайный характер. Эти возмущения вызывают отклонения регулируемого параметра y(t) за пределы области допустимых значений. Ставится задача определения параметров настроек регулятора и , обеспечивающих эффективное подавление системой автоматического регулирования влияния возмущений на регулируемый параметр. Показателем качества работы САР (критерием оптимизации) принимается вероятностная характеристика – среднеквадратическая ошибка:

.

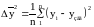Условием оптимальности является .

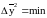Расчет 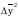в процедуре оптимизации САР выполняется по вероятностным характеристикам. Используя формулу обратного преобразования Фурье, получим:

,

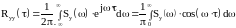где 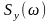- спектральная плотность ошибки .

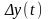При 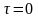получаем:

.

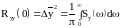Спектральная плотность рассчитывается по формуле:

,

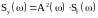где 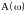– амплитудно-частотная характеристика САР по каналу; возмущение f (t) – регулируемая величина y(t), 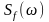– спектральная плотность сигнала возмущения f(t). В процедуре оптимизации в качестве f(t) используется случайная функция x(t) из процедуры идентификации.

Спектральная плотность 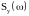наиболее просто определяется по ранее вычисленной автокорреляционной функции R_x(τ) по формуле прямого преобразования Фурье:

.

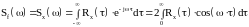Процедура оптимизации САР (движение по экспериментальной поверхности 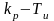) может выполняться любым градиентным методом оптимизации или методом Гаусса-Зайделя.