
Японские математики отыскали фракталы в экономических кризисах
Математики из Токийского университета установили, что финансовый рынок до и после обвала подчиняется тем же закономерностям, что и фазовые переходы в физике конденсированных сред. При этом, отмечают ученые, поведение биржевых индексов вблизи "критической точки" напоминает кардиограмму или кривую сейсмографа. Статья об этом была опубликована в журнале Physics Review Letters, сообщает сайт Американского физического института (AIP).
Считается, что за короткое время рынок испытывает колебания, которые подчиняются статистической схеме "случайных блужданий": вероятность конкретного отклонения тем меньше, чем больше само отклонение. Такой ситуации соответствует универсальная "гауссова формула", описывающая сумму независимых слагаемых одинаковой природы, если их достаточно много. "Неровность" графика, или усредненную амплитуду колебаний, экономисты называют волатильностью - эта величина является оценкой "стабильности" того или иного рыночного процесса.
Однако, как выяснили математики, рядом с критической точкой гауссов закон не соблюдается: колебания разной силы становятся равновероятными, а график оказывается фракталом, или "самоподобной кривой": он сам и любой его фрагмент статистически одинаковы, а волатильность перестает быть содержательной характеристикой. Аналогом этого называют, например, фазовый переход в магнитных материалах, когда при определенной температуре "магнитные моменты" отдельных атомов начинают спонтанно менять ориентацию.
Исходными данными для исследователей были значения биржевого индекса S&P-500 c 1984 по 1995 годы. На этот интервал приходится один из самых серьезных финансовых кризисов - "черный понедельник" 1987 года, когда биржевые индексы США и Великобритании снизились более чем на 20 процентов.
Подобные закономерности можно было бы использовать для предсказания обвалов, однако хорошо известно, что биржи довольно чувствительны к прогнозам - а следовательно, "математически выверенное" обещание обвала заведомо вызовет панику и обвал, которых в противном случае могло бы не быть.
В 1930 году, Ральф Нельсон Эллиот, после того как провел ни один год, анализируя данные по фондовым рынкам, сделал заключение, что ценовые тренды и их развороты формируют узнаваемые ценовые паттерны, после чего он выделил и классифицировал 13 таких паттернов и описал, как они формируют большие и меньшие разновидности самих себя. Это открытие он назвал волновым принципом. Сам же Эллиот не привязывал свою теорию к фракталам, он только сделал предположение, что движение цены САМОПОДОБНО по своей сущности и, основываясь на постулатах Доу, утверждал наличие циклов на финансовых рынках.
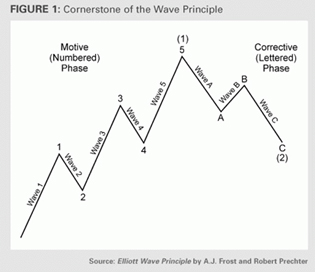
Цикл Эллиота
Основные принципы развития цикла Эллиота:
Цены финансового рынка развиваются в виде распознаваемых моделей.
Модели повторяются по форме.
Развитие принимает форму пяти волн особой структуры.
Три волны из них, обозначенные цифрами 1, 3, 5, действительно осуществляют направленное движение.
Волны 1, 3, 5 разделяются двумя противотрендовыми коррекциями, обозначенными цифрами 2 и 4.
Волна 2 никогда не заходит за начало волны 1.
Волна 3 никогда не бывает самой короткой.
Волна 4 никогда не заходит на территорию волны 1.
ЧИСЛА ФИБОНАЧЧИ И ХАРАКТЕРИСТИКИ ВОЛН Ральф Эллиот первым подал идею использовать числовую последовательность Фибоначчи для составления прогнозов в рамках технического анализа. С помощью чисел и коэффициентов Фибоначчи можно прогнозировать длину каждой волны и время ее завершения. Не затрагивая вопроса времени, обратимся к наиболее часто применяемым правилам определения длины Эллиотовских волн. Под длиной в данном случае имеется в виду ее повышение или понижение по шкале цен. Импульсные волны. Волна 3 обычно имеет длину, составляющую 1,618 волны 1, реже – равную ей. Две из импульсных волн часто бывают равны по длине, обычно это волны 5 и 1. Обычно это происходит, если длина волны 3 меньше, чем 1,618 длины волны 1. Часто встречается соотношение, при котором длина волны 5 равна 0,382 или 0,618 расстояния, пройденного ценой от начала волны 1 до конце волны 3. Коррекции Длины корректирующих волн составляют определенный коэффициент Фибоначчи от длины предшествующей импульсной волны. В соответствии с правилом чередования волны 2 и 4 должны чередоваться в процентном соотношении. Наиболее распространенным примером является следующий: волна 2 составила 61,8% волны 1, при этом волна 4 может составлять только 38,2% или 50% от волны 3.
