2.2 Алгоритмы с составными условиями

Вообще говоря, логический блок может содержать лишь одно условие и запись в блок-схеме алгоритма составного условия следующего вида:

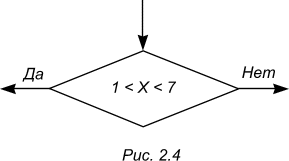
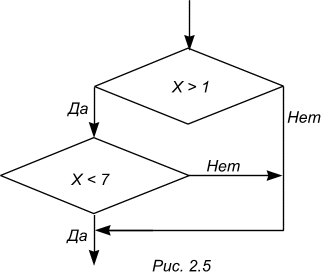
считается неверной, т.к. двойное неравенство содержит фактически два простых условия: X > 1 и X < 7 . Которые реализуются в блок-схемах алгоритмов в виде следующей последовательности:

Для упрощения реализации блок-схем алгоритмов мы будем в дальнейшем принимать блок-схемы с составными условиями, записанными в одном блоке, которые будем записывать в одном операторе используя не отдельные условия, а совокупность связанных между собой условий (отношений) и для их обозначения в алгоритме договоримся использовать символы «И», «ИЛИ», «НЕ», которые будем рассматривать как знаки логических операций, позволяющих из простых условий создавать составные.

Тогда рассмотренный выше пример с составным условием 1 < X < 7 будет на блок-схемах выглядеть следующим образом:

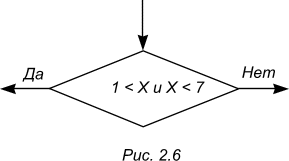
Cсоставное условие вида «А и В» (логическое умножение) истинно тогда и только тогда, когда истинны оба условия А и В, в остальных случаях ложно.

Составное условие «А или В» (логическое сложение) истинно тогда, когда истинно хотя бы одно условие - А или В.

Условие вида «не А» истинно, если условие А ложно, и наоборот.

Постановка задачи. Вычислить значение функции Y по одной из формул:

Метод решения этой задачи вытекает из определения составного условия «А и В» и выглядит следующим образом:

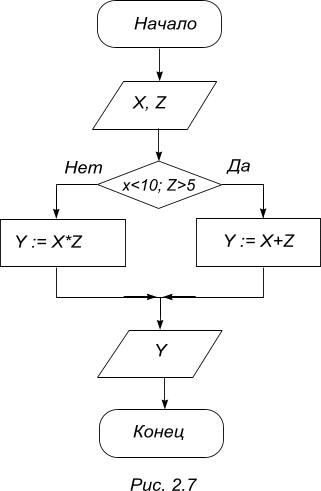
Вопросы для самопроверки

1. Как схематически изображается алгоритм разветвляющихся процессов?

2. Как называют возможное направление расчета?

3. Какого типа условия бывают в рассмотренных алгоритмах?

3 Алгоритмы циклических процессов

Часто при решении задач приходится многократно вычислять значения по одним и тем же математическим зависимостям для раз­личных значений входящих в них величин. Такие многократно по­вторяемые участки вычислительного процесса называются циклами. Использование циклов позволяет существенно сократить объем схемы алгоритма и длину соответствующей ей программы. Различают циклы с заданным и неизвестным числом повторений. К последним относятся итерационные циклы, характеризующиеся последовательным при­ближением к искомому значению с заданной точностью.

Для организации цикла необходимо выполнить следующие дей­ствия:

1. задать перед циклом начальное значение переменной, изме­няющейся в цикле;

2. изменять переменную перед каждым новым повторением цикла;

3. проверять условие окончания или повторения цикла;

4. управлять циклом, т. е. переходить к его началу, если он не закончен, или выходить из него по окончании.

Последние три функции выполняются многократно.

Переменная, изменяющаяся в цикле, называется параметром цикла. В одном цикле может быть несколько параметров.

Переменную, значения которой вычисляются машиной и хранят­ся в одной и той же ячейке памяти, называют простой переменной, а переменную, являющуюся элементом массива, - переменной с ин­дексом. Следует иметь в виду, что параметром цикла является при использовании простой переменной сама переменная, а при использо­вании переменной с индексом - ее индекс.

3.1 Оператор цикла со счетчиком

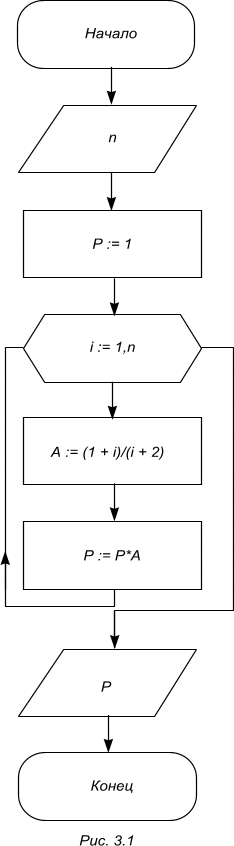
Рассмотрим построение алгоритма циклического процесса с использованием оператора цикла со счетчиком на примере.

Постановка задачи: дано натуральное число n, требуется вычислить произведение членов ряда:

.

Блок-схема алгоритма:

3.2 Оператор цикла с предусловием

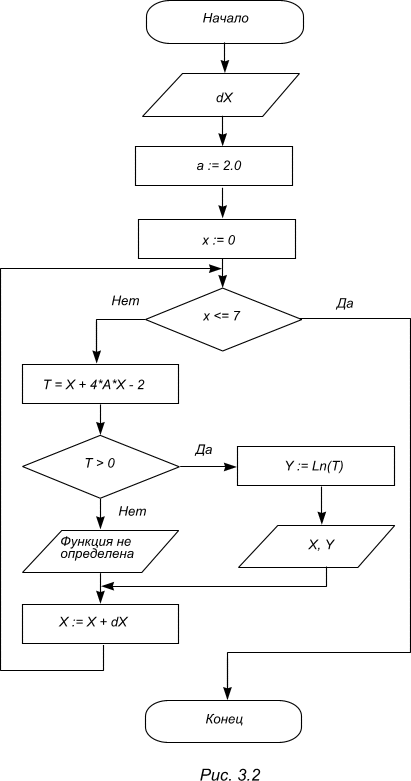
Постановка задачи: составить блок-схему алгоритма вычисления функции

если 0 dx = 1.0; a = 2.0.

Блок-схема алгоритма:

3.3 Оператор цикла с постусловием

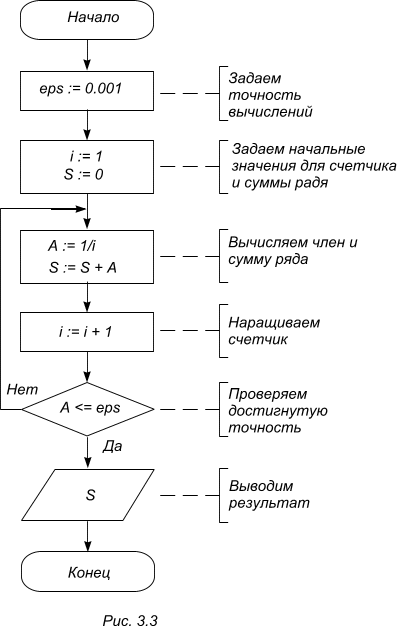
Постановка задачи: составить блок-схему алгоритма вычисления суммы членов ряд с погрешностью не более следующей бесконечной последовательности:

Блок-схема алгоритма:

3.4 Комбинация базовых команд при построении алгоритмов

Комбинация базовых команд. Известно, что любой алгоритм может быть построен с использованием только базовых конструкций: операторов следования, разветвления и цикла. Это превращает построение алгоритма в «сборку» его конструкций из имеющегося набора базовых конструкций.

Сборка алгоритма проводится двумя путями:

1. Базовые элементы могут соединяться в последовательность, образуя конструкцию следования.

2. Одна базовая конструкция может вкладываться в другую конструкцию, образуя вложенные конструкции.

Вспомогательные (подчиненные) алгоритмы. Часто при построении алгоритма оказывается возможным использовать уже разработанные ранее алгоритмы. Готовые алгоритмы, целиком включаемые в состав разрабатываемого алгоритма, называются вспомогательными или подчиненными алгоритмами в отличие от основного алгоритма, в состав которого они включаются. Эти алгоритмы оформляются соответствующим образом и называются подпрограммами или процедурами. В заголовке подчиненного алгоритма следом за именем может указываться в круглых скобках список формальных параметров. В списке формальных параметров указываются имена входных и выходных величин (аргументов и результатов) алгоритма. Это необходимо для того, чтобы при ссылке на подчиненный алгоритм можно было задать значения аргументов, а после исполнения подчиненного алгоритма – воспользоваться результатами - значениями соответствующих переменных.

Ссылка на вспомогательный алгоритм в основном алгоритме осуществляется с помощью специальной команды вызова вспомогательного алгоритма, в которой указывается имя подчиненного алгоритма и список фактических параметров, которые должны быть подставлены вместо формальных параметров при исполнении вспомогательного алгоритма.

Команда вызова вспомогательного алгоритма имеет вид:

<имя вспомогательного алгоритма> (<список фактических параметров>).

Исполнение такой команды эквивалентно исполнению вспомогательного алгоритма.