|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ ВЫСШИЙ КОЛЛЕДЖ ИНФОРМАТИКИ, ЭЛЕКТРОНИКИ И МЕНЕДЖМЕНТА (ВКИЭМ ТУСУР)
Контрольная работа №1 по дисциплине Идентификация и диагностика технических систем
Проверил: Чеботков А.И. _____________
Выполнил: Шевцов.А.С. гр. 918 _____________
Томск 2012
|
Содержание
Введение 3
Глоссарий 4
Задание 5
Решение 6
Заключение 12
Список литературы 13
Введение
Целью данной контрольной работы является изучение и нахождение собственных значений матриц, приобретения навыков по диагонализации систем с помощью матриц канонического преобразования, исследованию управляемости и наблюдаемости систем,
получению передаточных функций, используя преобразование Лапласса и с помощью
z- преобразования.
Глоссарий
detA |
Определитель матрицы |
λ |
Собственное значение матрицы |
A-1 |
Обратная матрица |
E |
Единичная матрица |
V |
Собственный вектор матрицы |
A* |
Преобразованная матрица |
AT |
Транспонированная матрица |
Rang|A| |
Ранг матрицы А |
|
Матрица строка |
|
Матрица столбец |
|
Квадратная матрица |
|
Единичная матрица |
G(s) |
Передаточная функция |
X(t) |
Входной сигнал |
Y(t) |
Выходной сигнал |
z-1 |
Оператор сдвига |
Задание
Задана система со скалярным входным и выходным сигналом:
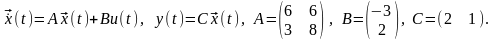
1.Преобразовать
систему с помощью матрицы преобразований
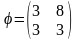 ,
найти собственные значения матрицы А
и преобразованной матрицы А*.
,
найти собственные значения матрицы А
и преобразованной матрицы А*.
2.Диагонализировать систему, найдя матрицу канонического преобразования.
3.Исследовать управляемость системы, используя результаты канонического преобразования.
4.Исследовать управляемость на основе полиномиального разложения матричной экспоненты.
5.Исследовать наблюдаемость, анализируя каноническую систему.
6.Исследовать наблюдаемость с помощью критерия на основе полиномиального разложения матричной экспоненты.
7.Получить передаточную функцию системы, используя преобразование Лапласа.
8.Построить
дискретную модель системы, используя
замену производной по времени приближенным
равенством
 ,
полагая, что
,
полагая, что
tk=0,1,2..; k=0,1,2..; Δt=1. Получить для этой модели передаточную функцию с помощью z-преобразования.
Решение
1)
det(A
-
λE)=
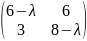 =(
=( )(
)( )
– 18= λ2
- 14λ + 30
)
– 18= λ2
- 14λ + 30
D=b2- 4ac= 76
Λ1= 11.36
Λ2= 2.64
Находим А* по формуле:
А*=φ-1×А×φ= =
=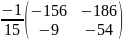 =
=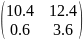 (1.1)
(1.1)
φ-1= =
=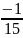
 (1.2)
(1.2)
φ*= (1.3)
φ11=3
φ21=8
φ12=3
φ22=3
detφ= 9-24= -15
det(A*
-
λ*
E)=
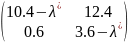 =(
=(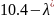 )(
)(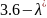 )
– 7.44=
)
– 7.44=
 2
- 14
+ 30
2
- 14
+ 30
D=b2- 4ac= 76
Λ1= 11.36
Λ2= 2.64
2)Используем формулу:
Λi= EV1=AV1 (2.1)
Для Λ1=2.64
2.64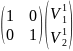 =
=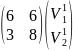
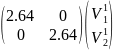 =
=
 =
=
2.64 =
=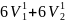 2.64
2.64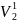 =
=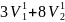
-3.36
=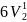 |÷(-3.36) -3.36
=
|÷(-3.36)
|÷(-3.36) -3.36
=
|÷(-3.36)


V1= =
=
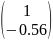
Для Λ2= 11.36
11.36 =
 =
=
 =
=
11.36 = 11.36 =
5.36
=
|÷(5.36) 3.36
=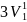 |÷(3.36)
|÷(3.36)
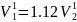

V1=
=
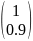
V=(V1,
V2)=
Λ=V-1AV (2.2)
V-1=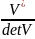 =
= =
=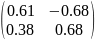
V*=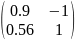
detV=1.46
λ= =
=
3)Используем формулу:
B*=V-1B= =
=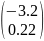 (3.1)
(3.1)
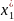 =
λ1
+ U(t)= 2.64
+ U(t)(-3.2)
=
λ1
+ U(t)= 2.64
+ U(t)(-3.2)
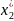 =
λ2
+ U(t)=
2.64
+ U(t)(0.22)
=
λ2
+ U(t)=
2.64
+ U(t)(0.22)
Система управляема, так как нет нулей.
4)Пользуемся формулами:
AB=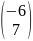
M= =
=
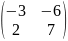 (4.1)
(4.1)
Вычисляем ранг матрицы А:
Шаг:1
Разделим строку 1 на a1,1 = |
6 |
Получим матрицу :
|
Шаг:2
Вычтем из строки 2 строку 1 умноженную на a2,1= |
3 |
Вычитаемая строка :
|
|
|
Модифицированная матрица :
|
Шаг:3
Разделим строку 2 на a2,2 = |
5 |
Получим матрицу :
|
Требуемый вид матрицы получен и ее ранг совпадает с рангом исходной. Проанализируем последнюю матрицу, в ней легко выделить невырожденную квадратную подматрицу (минор) порядка 2. Этот минор располагается с 1-й по 2-ю строку и с 1-го по 2-й столбец (см. ниже). Минор 2-го порядка :
|
|
|
Данный минор невырожденный (его определитель не равен нулю) т.к. определитель треугольной матрицы равен произведению диагональных элементов. Кроме того, из конечной матрицы нельзя выделить невырожденную подматрицу порядка больше чем 2, следовательно, ранг матрицы |A| равен 2 Ответ: rang|А|=2
Так как ранг матрицы равен двум, то данная система управляема.
5) Находим по формуле:
С*=СV= =
=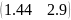 (5.1)
(5.1)
Так как нет нулей, то система наблюдаема.
6) Используем формулу:
L=( CT, ATCT)
AT=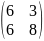
CT=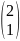
ATCT=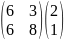 =
=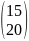
L=
Rang|L|= 2
Система наблюдаема.
7) Преобразуем уравнения, используя формулы:
Sx(S)=Ax(S) + BU(x) (7.1)
Y(S)= Cx(S) (7.2)

Y=
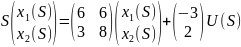
Y=
Передаточная функция имеет вид:
S(E - A)X(S)= BU(S) (7.3)
X(S)= (SE - A)-1BU(S) (7.4)
S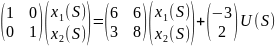

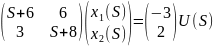
По формуле:
G(S)=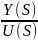 =C(SE - A)-1B
(7.5)
=C(SE - A)-1B
(7.5)
G(S)=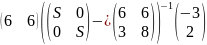 =
=
 =
=
=
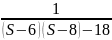
 =
=
 =
=
=
8) Находим по формуле:
T=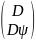 =
= (8.1)
(8.1)
 =
=
T-1=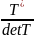 =
0,04
=
0,04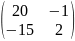 =
=
 =25
=25
Ψ*=TψT-1= =
= (8.2)
(8.2)
Ω*=TΩ= =
=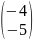 (8.3)
(8.3)
D*=DT-1= =
=
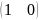
B1=-3
B2=2
A1=-30
A2=14
G(z)=
 (8.4)
(8.4)
G(z)=

Φ=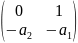 =
=
Г= B=
B=
X1(K)Ф11x(K-1) + Ф12x(K-1) +Г11U(K-1)
X2(K)Ф21x(K-1) + Ф22x(K-1) +Г12U(K-1)
-14x(K-1) + (K-1)U
x(K-1) + 30x(K-1) – 30U(K-1)
y=x1(K)
G=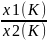 =
=