1 Положительное, 1 отрицательное

Запуск №2

Введите два числа

-1

-3

0 Положительных, 2 отрицательных

Задание №3

Дано целое число K и N ненулевых целых чисел. Найти и вывести на экран количество чисел в наборе, меньших K.

Постановка задачи

Входными данными являются:

• количество ненулевых целых чисел (N);

• число К (К).

• набор из N чисел (поскольку весь набор чисел сохранять программе не требуется, то для обработки набора можно использовать одну переменную А, в которую пользователь будет одно за другим записывать числа).

Выходные данные:

• количество чисел в наборе, меньших K (Kmn)

Словесное описание алгоритма.

1. Вывести на экран для пользователя сообщение о том, что нужно ввести количество элементов набора.

2. Записать введённое пользователем значение в переменную N.

3. Присвоить переменной Kmn начальное значение 0 (чисел меньших К пока не обнаружено).

4. Следующие далее команды 5, 6, 7 повторить N раз (для каждого из чисел, входящих в набор).

5. Вывести на экран для пользователя сообщение о том, что нужно ввести очередное число из набора.

6. Записать введённое пользователем значение в переменную А.

7. Если А<K, то увеличить значение переменной Kmn на единицу, в противном случае перейти к следующей команде.

8. Вывести на экран значение переменной Kmn.

Программа на языке Pascal.

program c;

var

N, Kmn, A, K:integer;

i:integer;

begin

writeln(‘Введите количество элементов в наборе’)

read(N);

writeln(‘Введите число К’)

read(K);

Kmn:= 0;

for i:=1 to N do

begin

writeln(‘введите число №’, i);

read (A);

if A<K then

Kmn:=Kmn+1;

end;

write(‘количество чисел в наборе, меньших K = ’, Kmn)

end.

Блок-схема алгоритма

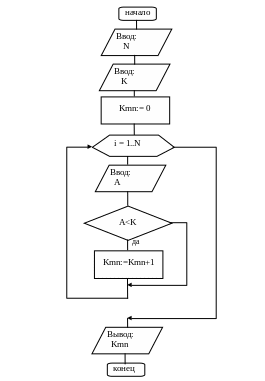
Результаты тестовых запусков:

Запуск №1:

Введите количество элементов в наборе

4

Введите число К

0

введите число №1

-1

введите число №2

1

введите число №3

10

введите число №4

-10

количество чисел в наборе, меньших K = 2

Запуск №2:

Введите количество элементов в наборе

3

Введите число К

5

введите число №1

0

введите число №2

5

введите число №3

15

количество чисел в наборе, меньших K = 1

Методика решения задач с помощью электронных таблиц ms Excel

Процесс разработки электронного документа (в нашем случае электронной таблицы Excel) для решения задачи можно разбить на следующие этапы:

1. Разработка структуры документа.

2. Реализация вычислений.

3. Представление полученных результатов.

Разработка структуры таблицы

Структура таблицы, её внешний вид и наполнение в некоторой степени зависит от вкуса разработчика. Понятие структуры таблицы можно разделить на следующие составляющие:

1. размещение ячеек с данными;

2. форматирование каждой ячейки, или групп ячеек (шапка, графа, столбец, заголовок и т. п.).

Понятие формат включает в себя набор атрибутов (свойств), использующихся для представления значений в ячейке, (например: вид шрифта; дополнительные символы, выводимые вместе с числом (“%”, “$”, “р.”); количество знаков после запятой в записи вещественного числа и т. п.), а также набор атрибутов, определяющих внешний вид ячейки (например: тип и цвет линии границы, фоновая заливка ячейки и т. п.). Соответственно форматирование – это процесс задания этих свойств, придание ячейке требуемого внешнего вида.

Обычно чётко разделить во времени этапы создания структуры таблицы не удается. Разработчик может разместить на листе часть данных таблицы, затем отформатировать её, после чего проделать то же для следующей части. Затем, обнаружив, что части не состыковываются, разработчик вынужден вернуться к форматированию первой части таблицы и т. д.

Такой подход, конечно, на первый взгляд нерационален, но чёткое разделение этих этапов требует тщательного предварительного планирования, что также ведёт к временным затратам и не гарантирует отсутствия ошибок, допущенных на этапе планирования.

Поэтому в данном разделе опишем основные приёмы размещения данных в таблице и её форматирования, а в разделе «Пример выполнения заданий средствами, Excel» приведём один из вариантов реализации.

Для ввода данных в заданную ячейку, нужно её активировать: установить на нее курсор, щёлкнув мышью. После этого можно начинать вводить данные.

Если информация уже введена в ячейку и нужно лишь отредактировать ранее введенные данные, то можно, дважды щёлкнув мышью на нужной ячейке, или нажав клавишу F2, когда требуемая ячейка выделена, перейти в режим редактирования данных ячейки.

Восстановить первоначальное содержимое ячейки в режиме ввода можно, нажав клавишу ESC. Восстановление данных и выход из режима ввода осуществляется при щелчке мышью по кнопке “Отмена”, расположенной в строке формул.

При вводе данных можно столкнуться с необходимостью вставки строки или столбца в таблицу. В Excel это можно выполнить следующим образом. Активируется ячейка столбца, перед которым нужно вставить новый столбец и вызывается команда Вставка | Столбец. Аналогично для вставки строки выполните команду Вставка | Строка.

Помимо столбцов и строк в таблицу можно вставлять и ячейки. Для этого выполните команду Вставка | Ячейки, с указанием направления сдвига остальных ячеек на листе.

Форматировать ячейки удобнее не по одной, а группами (блоками). Для выделения прямоугольного блока необходимо нажать левую кнопку мыши, переместить указатель и отпустить кнопку, когда будет выделено нужное количество ячеек.

Получить доступ к атрибутам формата в выделенных ячейках можно, выполнив команду Формат | Ячейки. В диалоговом окне Формат ячейки, все атрибуты размещены на нескольких вкладках. Форматы представления значений, записанных в ячейку, собраны на вкладке Число.

Для задания расположения текста в ячейке используется вкладка Выравнивание (рис. 2). Здесь можно установить параметры выравнивания и направления текста в ячейке. Здесь же имеется несколько переключателей. В таблице 1 представлен вид текста в ячейке при включении одного из переключателей.

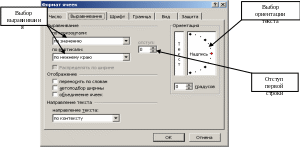
Рис. 2. Вкладка Выравнивание диалога Формат ячеек

Для изменения вида границы ячейки используется вкладка Граница или, для быстрого доступа к этой функции, кнопка с выбором на панели инструментов (рис. 3).

С помощью вкладки Шрифт можно задать цвет, размер, начертание текста в ячейке. Для задания цвета или способа заливки фона ячейки используется вкладка Вид.

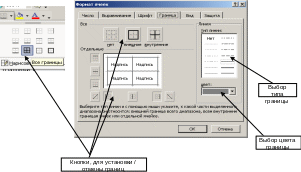
Рис. 3. Вкладка Граница диалога Формат ячеек

Таблица любой сложности, а также различные бланки и прочие документы, в конечном счёте, для Excel являются совокупностью различным образом отформатированных ячеек. Приёмов, описанных в данном разделе, вполне достаточно для составления простых электронных документов Excel.

Вычисления в таблице

После того, как готова структура таблицы, можно перейти к заполнению формулами ячеек, предназначенных для размещения промежуточных и выходных данных.

Формулой или выражением в Excel называется последовательность символов, начинающаяся со знака равенства “=”. В эту последовательность символов могут входить константы, ссылки на ячейки, вызовы функций и знаки операций.

Результатом работы формулы является новое значение, которое отображается в ячейке.

Ссылка – это адрес, который однозначно определяет ячейку или диапазон ячеек листа Excel. Ссылки могут использоваться везде, где необходимо получить значение, или массив значений, из электронной таблицы.

Функции в Excel используются для выполнения стандартных вычислений в рабочих книгах. Значения, которые используются для вычисления функций, называются аргументами. Аргументы записываются в круглых скобках сразу за названием функции и отделяются друг от друга символом точка с запятой “;” Значения, возвращаемые функциями в качестве ответа, называются результатами.

Имя_функции (аргумент1; аргумент2; ...)

В качестве аргументов можно использовать выражения или константы. Функции, являющиеся аргументом другой функции, называются вложенными. В формулах Excel можно использовать до семи уровней вложенности функций.

Тип аргумента, используемого функцией, зависит от конкретной функции. Некоторые функции могут иметь необязательные аргументы, которые могут отсутствовать при вызове функции.

Например, о формуле =(B4+C4)/2-ОКРУГЛ((B4+C4)/2;1) можно сказать, что в неё входят ссылки на ячейки В4 и С4, константы 2 и 1, вызов функции ОКРУГЛ, первый аргумент которой является выражением (B4+C4)/2, а второй константой 1, функция ОКРУГЛ возвратит результат вычисления выражения, округлённый до 1 знака после запятой.

Представление результатов в виде диаграммы

Диаграмма – средство графического представления числовых данных. В Excel диаграмма представляет собой графическое изображение, которое размещается на отдельном листе или поверх основной таблицы, в последнем случае её можно свободно перемещать и изменять размер, не искажая таблицу.

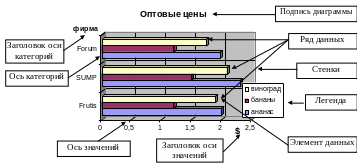
Рис. 4. Объекты, входящие в диаграмму

В первом приближении диаграмма создаётся с помощью мастера диаграмм – специальной программы, которая позволяет создать диаграмму пошагово уточняя её параметры, (подробнее работа с мастером диаграмм рассмотрена в разделе «Пример выполнения задания средствами Excel», стр. 25).

На втором этапе корректируют отдельные элементы диаграммы (см. рис. 4), каждый из которых имеет набор собственных атрибутов (свойств), которые определяют его внешний вид (положение, цвет, шрифт, выравнивание, рамки и т.п.). Доступ к этим атрибутам можно получить, выделив объект на диаграмме и вызвав команду Формат | Выделенный <Название объекта> (Например: Формат | Легенды...).

После того, как диаграмма приобретёт требуемый вид, остаётся только поместить её на листе так, чтобы она не мешала просмотру основной таблицы и результатов вычислений.

Оформление отчёта о решении задачи средствами Excel

Отчёт о решении задачи должен содержать:

1. полный текст задания;

2. описание использованных приёмов форматирования и функций, использованных для реализации вычислений в таблице;

3. распечатку готовой таблицы;

4. распечатку таблицы с демонстрацией формул в вычисляемых ячейках;

5. описание построения диаграммы;

6. изображение готовой диаграммы.

Пример выполнения задания средствами Excel

Задание

Имеются данные о некоторых деталях обуви и сведения о количестве пар обуви, выпускаемом некоторой организацией:

№	Наименование	Материал	Общая площадь деталей для производства пары обуви по размерам, дм2				Среднеассортиментная площадь дм2
225	232	240	247
	1	2	3	4	5	6	7
1	Союзка	ИК “Costo”	2,156	2,272	2,392	2,512
2	Накладной носок	ИК “Bravo”	4,724	4,976	5,24	5,508
3	Язычок	ИК “Costo”	3,756	3,756	4,016	4,016
4	Подблочник	ИК “Bravo”	3,456	3,456	4,208	4,208
5	Общая площадь заготовок, дм2

1. Общую площадь заготовок (графа 5).

2. Среднеассортиментную площадь деталей (столбец 7).

3. Подсчитать количество деталей, изготовленных из материала ИК “Costo”.

4. Подсчитать общую площадь материала ИК “Bravo”, используемого для производства обуви размера 225.

5. Сколько процентов от общей площади деталей обуви размера 240 составляют детали, выполненные из материала ИК “Costo”.

6. Определить, какая из деталей, язычок или подблочник, имеет большую среднеассортиментную площадь.

7. Построить диаграмму, представляющую площадь накладных носков обуви каждого размера.

Описание использованных приёмов форматирования и функций, использованных для реализации вычислений в таблице

Лист будет разделён на несколько частей: B3:I4 – шапка таблицы, В5:I10 – раздел данных таблицы.

Задание структуры шапки таблицы.

Как видно из задания – некоторые элементы шапки занимают две или более смежных ячеек (например, заголовок столбца «Материал», или «Общая площадь деталей для производства пары обуви по размерам»).

Для объединения двух или более смежных ячеек выделяем их, выбираем в меню Формат команду Ячейки и устанавливаем режим объединение ячеек.

Форматирование шапки таблицы.

Выделим все ячейки шапки, выбираем в меню Формат команду Ячейки, переходим на вкладку Выравнивание и установим для них параметры выравнивание по горизонтали и вертикали в положение по центру. Затем, переходим на вкладку Граница и устанавливаем внешние и внутренние границы в виде жирной линии.

После этого заполняем шапку таблицы согласно заданию.

Задание структуры раздела данных таблицы.

Описанным выше способом создаём объединённую ячейку для заголовка столбца «Общая площадь заготовок».

Форматирование раздела данных таблицы.

Выделяем ячейки раздела данных таблицы и выбираем в меню Формат команду Ячейки, переходим на вкладку Выравнивание, устанавливаем параметры выравнивание по горизонтали и вертикали в положение по центру. Переходим на вкладку Граница и устанавливаем внешние границы в виде жирной линии, а внутренние – в виде обычной линии.

Выделяем ячейки столбцов 1 и 2, выбираем в меню Формат команду Ячейки, переходим на вкладку Выравнивание, устанавливаем параметр выравнивание по горизонтали в положение по левому краю.

Выделяем ячейки с номерами столбцов и щёлкнем по кнопке с буквой «Ж» на панели инструментов для того, чтобы выделить цифры жирным. Аналогично поступаем с ячейками, содержащими номера строк.

После заполнения таблицы данными и регулирования размеров столбцов получим таблицу, представленную на рис. 5.

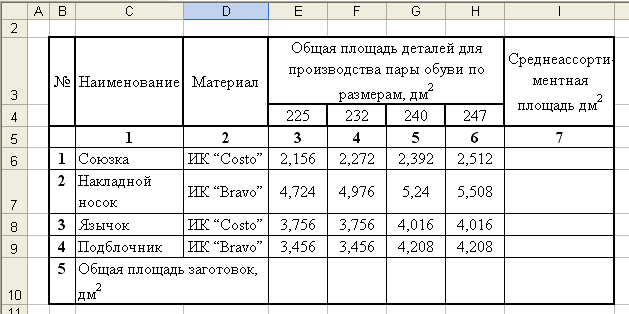
Рис. 5. Структура таблицы с исходными данными

Реализация вычислений

1. Общую площадь заготовок (графа 5).

Требуется заполнить строку с номером 5 формулами, вычисляющими сумму значений площадей заготовок по каждому размеру.

Для суммирования значений из нескольких ячеек можно использовать функцию СУММ.

В ячейку Е10 записываем формулу =СУММ(E6:E9), где E6:E9 - диапазон ячеек, содержащий площади деталей обуви размера 225.

Скопируем эту формулу в ячейку F10. Так как при составлении формулы были использованы относительные ссылки (Е6 и Е9), то при копировании они изменятся и формула примет вид =СУММ(F6:F9), где E6:E9 – диапазон ячеек, содержащий общую площадь деталей обуви, но уже для размера 232.

Скопируем данную формулу также и в ячейки G10, H10.