2.3. Методы проецирования земной поверхности
Для составления топографических карт и планов точки земной поверхности проецируют на поверхность референц-эллипсоида или на плоскость. Проецирование на поверхность референц-эллипсоида выполняется вдоль отвесных линий. Четырехугольник аbcd, полученный проецированием на сферическую поверхность эллипсоида, называют горизонтальной проекцией четырехугольника ABCD местности (рис. 2.4).
Рис. 2.4 |
Рис. 2.5 |
Рис. 2.6 |
При проецировании небольших по площади участков местности, основную уровенную поверхность можно принимать за плоскость. В таком случае отвесные линии можно считать параллельными между собой и горизонтальная проекция практически преобразуется в ортогональную. Согласно рис. 2.5 отрезки ab, bc, cd,…являются ортогональными проекциями соответствующих линий AB, BC, CD,…, углы abc, bcd,…– ортогональными проекциями соответствующих углов ABC, BCD,…, а плоский многоугольник abcd – ортогональной проекцией пространственного многоугольника ABCD. Положение точек и линий местности АВ,ВС,… в ортогональной проекции определяется длинами горизонтальных проложений ab,bc,…и горизонтальными углами между ними.
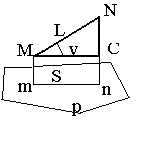
Длина ортогональной проекции линии местности MN на горизон-тальную плоскость p называется горизонтальным проложением S этой линии (рис. 2.6) и вычисляется из прямоугольного треугольника MNC по формуле S = L×cos ν.
Угол ν между линией местности MN и ее ортогональной проекцией на горизонтальную плоскость S = mn, измеряют непосредственно и называют углом наклона линии. Ортогональные проекции линий на плоскость при ν ≠ 0 всегда меньше соответствующих им отрезков на физической поверхности Земли.
2.4. Размеры участков земной поверхности, принимаемые за плоскость
Р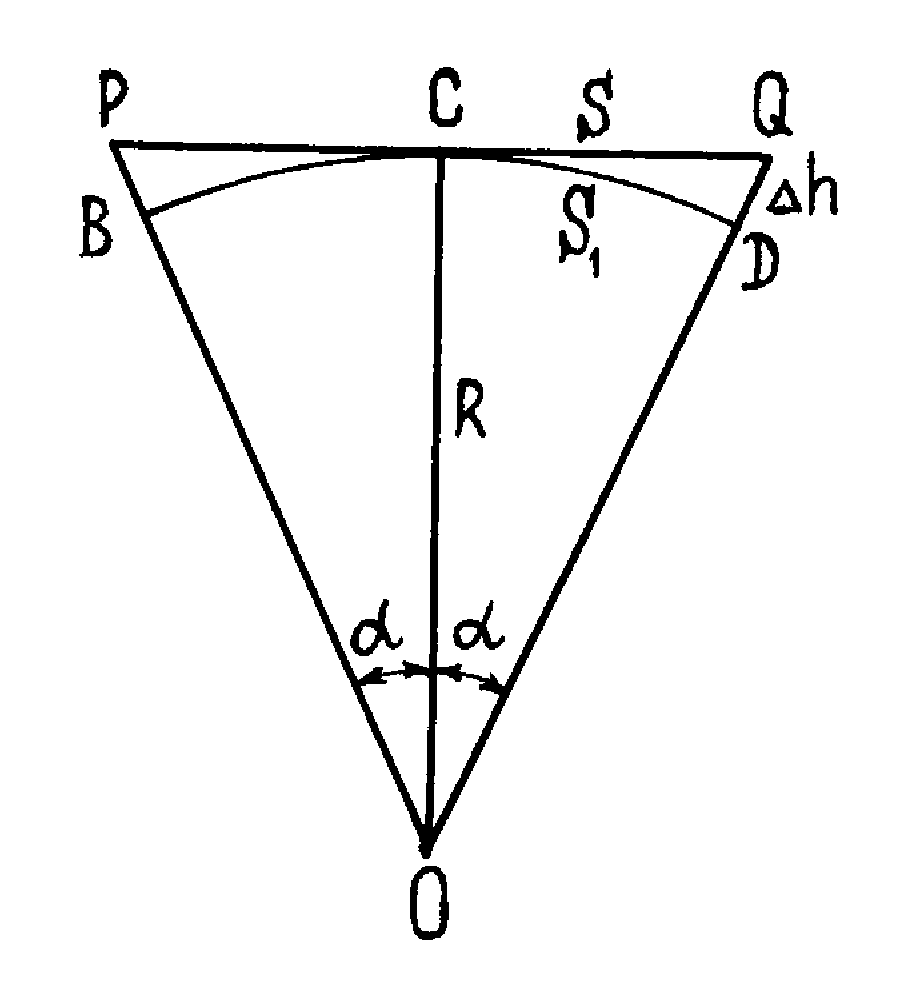
ассмотрим,
для каких по размерам участков местности
можно применять ортогональное
проецирование, т. е. при которых
кривизна Земли может не учитываться в
процессе создания карты или плана. На
рис. 2.7 изображена часть поверхности
Земли в виде дуги BCD
радиуса R и
ее проекция PQ
на плоскость
PCQ,
где PC = CQ.
Д
Рис. 2.7
Определим разность между длиной касательной S и длиной дуги S1. Выразим угол a в радианах, тогда согласно рис. 2.7 получим, что S = R × tga, а S1 = R×a. Откуда следует, что
DS = R(tga -a). (2.1)
Центральный
угол a по своей
величине незначителен. Поэтому при
разложении tga
в убывающий ряд можно ограничиться
вторым членом ряда и пренебречь
последующими из-за их незначительности.
Тогда
.
Подставим это значение в формулу 2.1. В
результате получим, что
.
(2.2)
Из формулы S1=R×a
получим, что
и заменим a в
формуле 2.2. Окончательно найдем,
что
.
(2.3)
Из
рис. 2.7 видно, что точка D находится
на уровенной поверхности и ее высота
равна нулю. Определим величину отрезка,
характеризующего отклонение точки Q
от уровенной поверхности. Для этого
рассмотрим прямоугольный треугольник
OCQ, откуда (R + h)²
= S² +
R². Упростив
данное равенство, имеем
.
Ввиду малого значения h
в сравнении с 2R окончательно
получим, что
.
(2.4)
Сравнивая формулы 2.3 и 2.4 видно, что значение h существенно больше DS. Если условно принять радиус Земли постоянным, то можно вычислить расхождения DS между длинами дуг на уровенной поверхности и их проекциями на плоскость, а также отклонения высот точек h от их положения на поверхности сферы из-за кривизны Земли (табл. 2.2).
Таблица 2.2
S , км |
DS ,м |
h, м |
1 |
0,00 |
0,08 |
5 |
0,00 |
1,96 |
10 |
0,01 |
7,85 |
20 |
0,07 |
31,39 |
50 |
1,02 |
196,20 |
Значение величины DS возрастает незначительно. При дуге 11 км DS составляет лишь 1:1 000 000 ее длины. Относительная погрешность измерения расстояний современными приборами составляет порядка 1:1 000 000. Поэтому принято считать, что участок радиусом 11 км можно принимать за плоскость, а при определении превышений между точками местности необходимо вводить поправку h.