3.3. Масштабы планов и карт

Масштабом плана называется отношение длины линии на плане к соответствующей длине горизонтального проложения этой линии на местности.

Как известно, планы составляются для небольших по площади территорий и поэтому их масштаб можно считать величиной постоянной. На картах следует учитывать искажения длины линий из-за кривизны Земли. Например, для проекции Гаусса–Крюгера поправки вычисляются по формуле 3.1. и при необходимости вводятся в измеренные линии.

Масштаб на планах и картах выражается в численной, именованной и графической формах.

Численный масштаб выражается простой дробью, в числителе которой единица, а в знаменателе число, показывающее во сколько раз горизонтальное проложение линии местности уменьшено при нанесении на план (карту). Масштабы могут быть любыми. Но чаще используются их стандартные величины: 1:500; 1:1000; 1:2000; 1:5000; 1:10 000; 1:25 000; 1:50 000; 1:100 000; 1:200 000; 1:300 000; 1:500 000; 1:1000 000. Например, масштаб карты 1:10 000 указывает, что горизонтальное проложение линии уменьшено на карте в 10 000 раз, т. е. 1 см на плане соответствует 10 000 см на горизонтальной проекции местности. Чем меньше знаменатель численного масштаба, тем крупнее считается масштаб, и наоборот. Численный масштаб величина безразмерная; она не зависит от системы линейных мер, т. е. им можно пользоваться, проводя измерения в любых линейных мерах.

Именованный масштаб представляет краткое словесное выражение численного масштаба и указывает, какая величина горизонтального проложения местности соответствует 1 см на плане (карте). Например, «в 1 сантиметре 100 метров».

Л

Рис. 3.3

инейный масштаб представ­ляет собой графическое выражение численного и именованного масшта­бов в виде линии, разделенной на равные отрезки – основания. Левый из них ab делится на 10 равных частей (десятые доли). Сотые доли оцениваются «на глаз». На рис. 3.3 показан линейный масштаб с основанием ab = bc = cd…, соответствующий численному масштабу 1:10 000.

Основание линейного масштаба выбирается таким образом, чтобы выражало целое число метров горизонтального проложения линии. В нашем примере оно равно 1 см.

Для более точного измерения линий на плане или карте пользуются поперечным масштабом (рис. 3.4). Для построения поперечного масштаба, на прямой МЕ откладывают отрезки AM = AB = BC = CD = DE, принимаемые за основание масштаба. В точках М, А, В,…, Е восстанавливают перпендикуляры и на крайние из них наносят 10 равных между собой отрезков Ме = Ее = еf = …. Через полученные точки е, f, p, g проводят прямые, параллельные МЕ. Нижнее и верхнее основание масштаба МА и NQ разбивают на 10 равных частей. Точки деления соединяют между собой параллельными наклонными линиями в следующем порядке: точку А с точкой Р, точку N с точкой F и так далее.

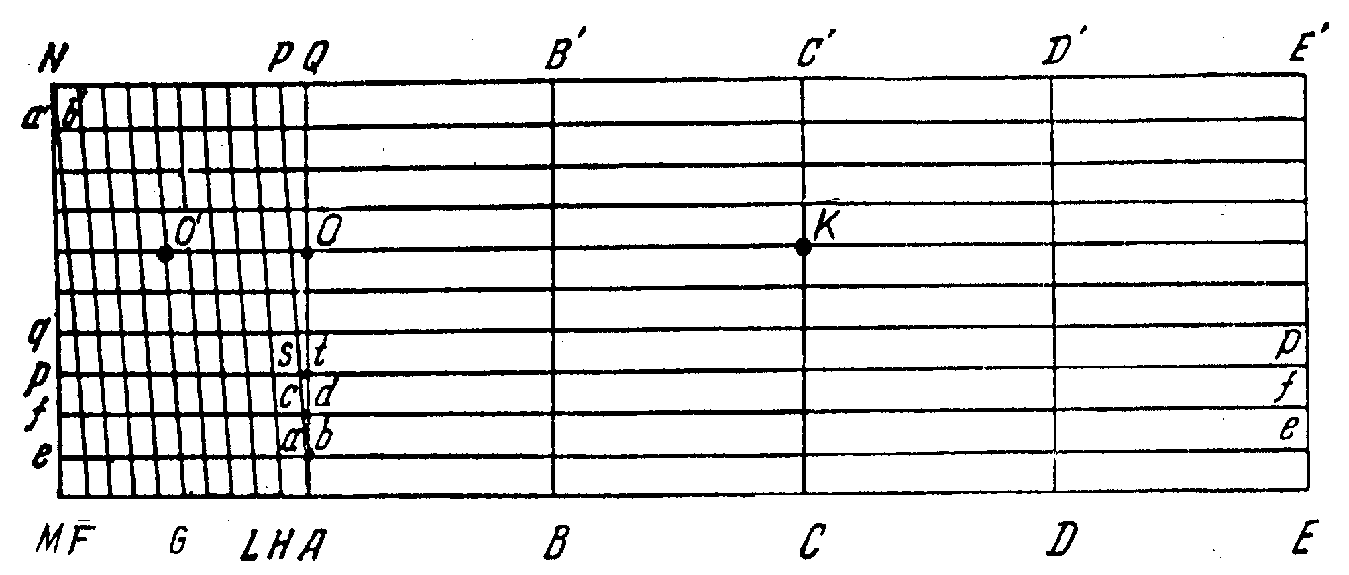
Рис. 3.4

Прямая АР и параллельные ей линии называются трансверсалями. Отрезок аb называют наименьшим делением поперечного масштаба. По построению малые отрезки АН, МF, PQ и др. будут равны 0,1 основания масштаба МА, а наименьшее деление аb будет равно 0,1 отрезков АН, МF, PQ и т. д. или 0,01 основания масштаба МА.

Пример: По поперечному масштабу с основанием равным 2 см определим расстояние О'К (рис. 3.4). При численном масштабе 1:10000 основанию в 2 см на плане будет соответствовать 200 м на местности, малые отрезки будут равны 20 м, а наименьшие – 2 м. Таким образом, ОК = 200 м × × 2 = 400 м; малых делений – 5, тогда AG = 20 м × 5 = 100 м и измеряемая линия О'К находится на шестой горизонтальной линии, т. е., 2 м × 6 = = 12 м. Таким образом, измеряемая линия О'К равняется 512 м.

При измерениях длины линий на картах, измеряемая линия берется в раствор циркуля-измерителя и переносится на поперечный масштаб. Необходимо, чтобы правая ножка измерителя находилась на одном из перпендикуляров (справа от основания МА), а левая – на пересечении трансверсали и горизонтальной линии основания МА, при этом обе ножки измерителя должны располагаться на одной горизонтальной линии О'К. Пользуясь поперечным масштабом измеряют длины прямых линий.

Измерение кривых линий производится двумя способами: при помощи курвиметра и циркулем-измерителем.

При первом способе колесико курвиметра прокатывают по измеряемой линии на карте. Стрелка прибора показывает отмеренное колесиком расстояние в сантиметрах (или дюймах). Пользуясь масштабом, определяют расстояние на местности. При измерении длин сильно извилистых линий сложно точно вести колесико по мелким изгибам, в связи с этим точность измерений курвиметром невысока.

При измерении длины кривых линий более точные результаты получают пользуясь вторым способом – применяя циркуль-измеритель с микрометренным винтом. Измерения выполняют малыми растворами измерителя (1–4 мм). Перед измерениями определяют цену раствора измерителя, т. е. измеряют линию, длина которой известна (обычно расстояние между километровыми сетками).

Точность масштаба. Предельные размеры предметов, которые можно различать на плане (карте) определяются графической точностью масштаба. Свойство человеческого зрения позволяет различать точку величиной порядка 0,1 мм. Это связано с критическим углом человеческого зрения, равным 1'. Поэтому расстояние на местности, соответствующее 0,1 мм плана, называют предельной точностью масштаба и ее величина t в метрах зависит от масштаба карты, т. е. t = 0,0001 М, где М – знаменатель масштаба карты. Например, для карты масштаба 1:10 000 предельная точность равна t = 0,0001  10 000 = 1м, а для карты масштаба 1: 50 000 – t = = 5м. Практически средняя ошибка измерения длин линий на карте составляет 0,3–0,4мм или 0,0003–0,0004 М.