- •7. Приборы для измерения давления
- •8. Сила давления жидкости на плоскую стенку произвольной формы
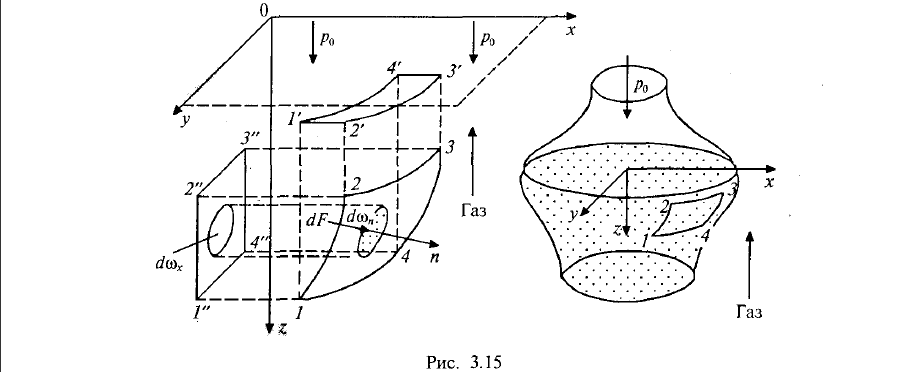
- •Сила давления жидкости на криволинейную стенку.
- •Простые гидравлические машины. Гидравлический пресс.
- •Закон Паскаля.
- •Закон Архимеда.
- •13. Условия плавучести и устойчивости тел, частично погруженных в жидкость.
- •14. Виды движения жидкости.
- •15. Струйка, поток жидкости, расход, живое сечение.
- •20. Геометрический и энергетический смысл уравнения Бернулли
- •21. Практическое применение уравнения Бернулли.
- •22. Виды гидравлических потерь.
- •23. Общие формулы для определения потерь напора.
- •24. Ламинарный режим течения жидкости.
- •Турбулентный режим течения жидкости.
- •Напряжения, скорость, потери при ламинарном течении.
- •Турбулентное течение в шероховатых трубах.
- •Характерные зоны движения жидкости. Опыты Никурадзе.
- •Формулы для определения коэффициента гидравлического трения.
- •Местные потери напора.
1. Предмет «общая гидравлика». Краткая история его развития.



Силы, действующие в жидкости.


Основные свойства капельных жидкостей.



Гидростатическое давление и его свойства.



Основное уравнение гидростатики.
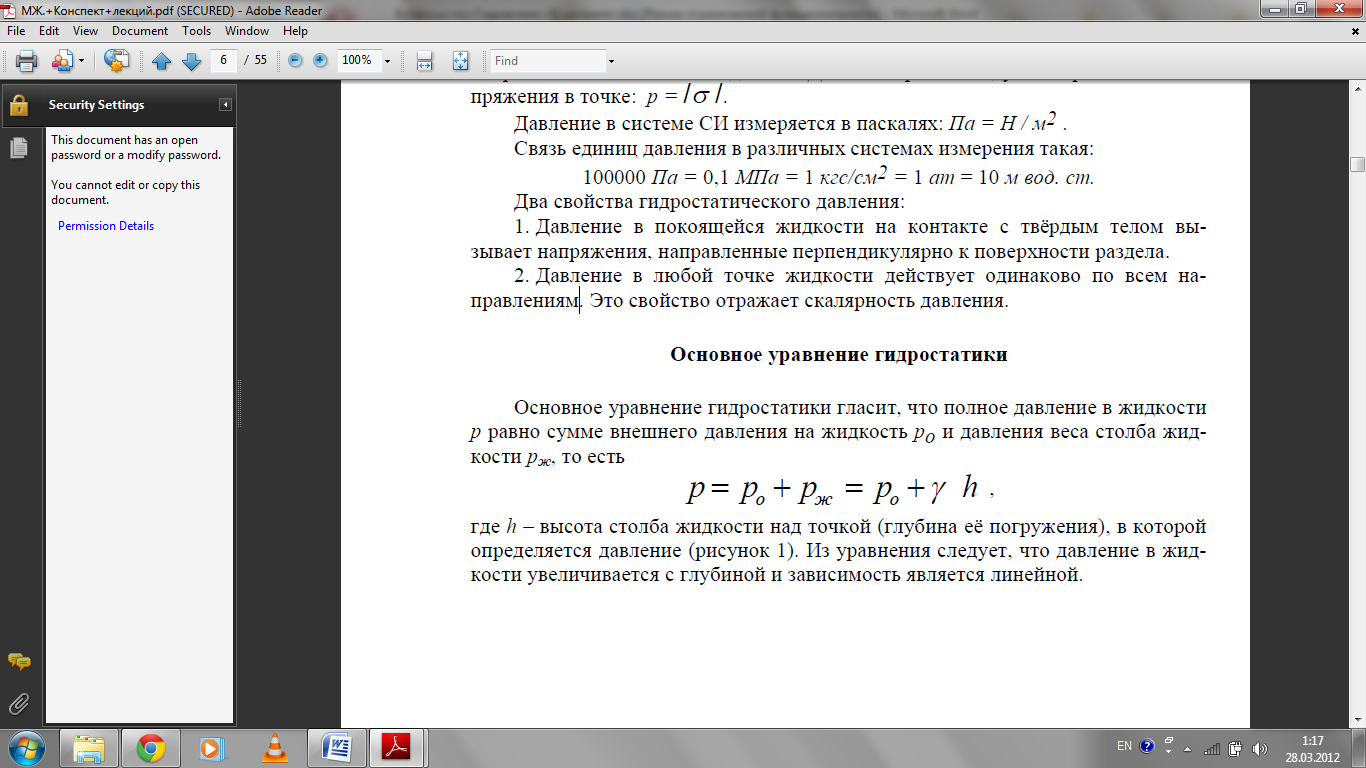

Дифференциальные уравнения равновесия жидкости.
![]() Система
уравнений Эйлера (уравнения
равновесия) определяет закон распределения
давления в покоящейся жидкости вдоль
соответствующей оси координат.
Система
уравнений Эйлера (уравнения
равновесия) определяет закон распределения
давления в покоящейся жидкости вдоль
соответствующей оси координат.
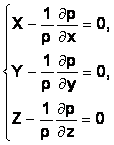
здесь X,Y,Z – напряжения массовых сил в проекциях на соответствующие оси координат x, y, z,
p – давление в соответствующей точке жидкости,
ρ - плотность жидкости.
Из уравнений Эйлера можно получить следующий вид основного дифференциального уравнения равновесия жидкости
7. Приборы для измерения давления
Давление в жидкости измеряется приборами:
пьезометрами,
манометрами,
вакуумметрами.
Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере P = 1 кгс/см2 = 0,1 МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления р необходимо к манометрическому давлению рман прибавить атмосферное давление Pатм снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной Pатм =101325 =100000 Па.
Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рисунке 2), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометре hp является показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению
Pизб=γhp
Где hp - пьезометрический напор (высота), м
Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов.
8. Сила давления жидкости на плоскую стенку произвольной формы
Пусть имеется фигура произвольной формы площадью со в плоскости 0l, наклоненной к горизонту под углом α (рис. 3.17).
Для удобства вывода формулы для силы давления жидкости на рассматриваемую фигуру повернем плоскость стенки на 90° вокруг оси 0l и совместим ее с плоскостью чертежа. Выделим на рассматриваемой плоской фигуре на глубине h от свободной поверхности жидкости элементарную площадку dω. Тогда элементарная сила, действующая на площадку dω, будет
dF= (p0 + γh) dω
 Интегрируя
последнее соотношение, получим суммарную
силу давления жидкости на плоскую
фигуру:
Интегрируя
последнее соотношение, получим суммарную
силу давления жидкости на плоскую
фигуру:
F=![]()
Рис 137
Учитывая, что h=l sinα, получим
F=![]()
или
F=
p0ω+
γ
l
sinα![]()
Последний интеграл равен статическому моменту площадки со относительно оси 0у, т. е.
=lc![]() ,
,
где lc — расстояние от оси Оу до центра тяжести фигуры. Тогда
F= p0ω+ γ l sinα ω
Так как lc sinα=hc
F=![]()
т. е. суммарная сила давления на плоскую фигуру равна произведению площади фигуры на гидростатическое давление в ее центре тяжести.
Точку приложения суммарной силы давления (точка d, см. рис. 3.17) называют центром давления. Центр давления находится ниже центра тяжести плоской фигуры на величину эксцентриситета е.
 Последовательность
определения координат центра давления
и величины эксцентриситета изложена
в § 3.15.
Последовательность
определения координат центра давления
и величины эксцентриситета изложена
в § 3.15.
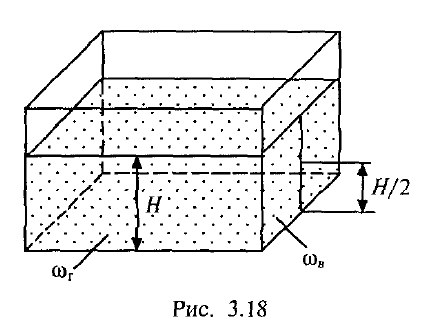
F=(po+γH)ωв
В частном случае вертикальной прямоугольной стенки получим (рис. 3.18)
F=(po+γH)ωr
Сила давления жидкости на криволинейную стенку.