Алгоритм "Селигер"

1. Привести систему уравнений к нулевому виду (исходная система).

2. Заполнить карту Карно нулями в соответствии с термами левых частей исходной системы уравнений, а в оставшиеся клетки вписать единицы. Эти единичные термы представляют собой СДНФ полной единицы системы.

3. Произвести минимизацию совокупности единичных термов. Полученное соотношение представляет МДНФ уравнения полной единицы системы.

4. Построить сокращённую (только для единичных термов) таблицу истинности уравнения полной единицы и выписать из неё все значения входных и выходных переменных в виде частных таблиц истинности для искомых функций.

5. Произвети минимизацию искомых функций.

Пример 1

Рассмотрим 1-ю задачу Порецкого[2]. Между птицами данного зоосада существуют 5 отношений:

1. Птицы певчие - крупные или обладающие качеством Y.

2. Птицы,не имеющие качества Y - или не крупны, или не имеют качества X.

3. Птицы певчие в соединении с крупными объединяют всех птиц с качеством X.

4. Каждая не-крупная птица есть или певчая,или обладающая качеством X.

5. Между птиц с качеством X совсем нет таких птиц с качеством Y,которые не будучи певчими, были бы крупны.

Определить, были ли птицы качества X певчие или нет. Узнать то же в отношении птиц качества Y. Найти, были ли среди птиц качества X птицы качества Y и наоборот.

Решение

Прежде всего необходимо отметить,что все 5 отношений являются по существу общеутвердительными и общеотрицательными посылками сорита,т.е.фактически речь идет о синтезе заключения в сорите.

Пусть X - птицы качества X,

Y - птицы качества Y,

S - певчие птицы,

G - крупные птицы.

Тогда условие задачи будет представлено следующими рекурсивными уравнениями[2](здесь и далее апостроф обозначает отрицание):

1. s=(g+y)s;

2. y'=(g'+x')y';

3. x(s+g)=x;

4. g'=(s+x)g';

5. xys'g=0.

Уравнения Порецкий через эквивалентность приводит к единичной форме:

1. g+y+s'

2. g'+x'+y

3. s+g+x'

4. s+g+x

5. x'+y'+s+g'

Основываясь на введенном нами русском базисе силлогистики[3] Axy = x'+y и Exy = x'+y', созданном при помощи скалярных диаграмм, можно получить эти же соотношения более простым путем :

1. As(g+y) = s'+g+y

2. Ay'(g'+x') = y+g'+x'

3. Ax(s+g) = x'+s+g

4. Ag'(s+x) = g+s+x

5. Ex(ys'g) = x'+y'+s+g'

Однако восхищает красота решения задачи П.С.Порецким без привлечения современной математической логики. Фактически русский ученый впервые в мире вывел соотношения для силлогистических функторов Аху и Еху в виде:

Axy = (x = xy),

Exy = (x = xy').

После раскрытия скобок по формуле эквивалентности мы получим формулы русского базиса[3]. Современная силлогистика до сих пор не замечает и не использует этих результатов великого русского логика. Кроме того, данная система уравнений представляет из себя 5 посылок силлогизма, точнее сорита.Таким образом, решив систему уравнений,Порецкий впервые в мире синтезировал аналитически заключение силлогизма(сорита).

Полная логическая единица всей задачи определяется Порецким как конъюнкция всех левых частей системы логических уравнений .Эту рутинную операцию можно заменить на менее утомительную процедуру построения дизъюнкции нулей.Получим систему[4]:

1. g'y's=0

2. gxy'=0

3. g's'x=0

4. g's'x'=0

5. gs'xy=0

Полный логический нуль системы равен дизъюнкции всех левых частей системы логических уравнений .Проведем решение задачи Порецкого с использованием карты Карно.Заполним карту Карно нулями в соответствии с нулевыми термами системы,а в оставшиеся клетки впишем единицы. Тогда минимальная дизъюнктивная нормальная форма (МДНФ) полной логической единицы всей задачи примет вид:

M=sy+gx'

xy

\ 00 01 11 10

gs \------------------+

00¦ 0 ¦ 0 ¦ 0 ¦ 0 ¦

+----+----+----+---+

01¦ 0 ¦ 1 ¦ 1 ¦ 0 ¦

+----+----+----+---+

11¦ 1 ¦ 1 ¦ 1 ¦ 0 ¦

+----+----+----+---+

10¦ 1 ¦ 1 ¦ 0 ¦ 0 ¦

+------------------+

Рис.1

Выпишем из карты Карно все единичные термы в виде таблицы истинности (табл.1). По табл.1 построим табл.2 для x = f1(g,s),табл.3 для y = f2(g,s) и табл.4 для y = f3(x). Если на каком-либо наборе функция принимает значение как 0, так и 1, то в соответствующую клетку карты Карно вписываем i. Если какой-либо набор отсутствует, то для этого набора в карту Карно вносим значение j при четырехзначной логике[4]. Карты Карно для табл.2,3 и 4 представлены на рис.2,3 и 4 соответственно.

Табл.1 Табл.2 Табл.3 Табл.4

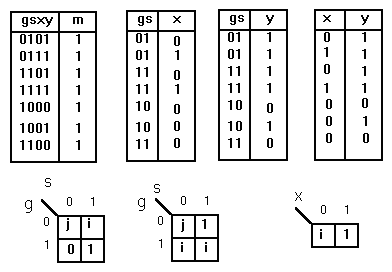
Рис.2 Рис.3 Рис.4

После минимизации получим для четырехзначной логики систему уравнений[4] :

x = is + jg's'

y = g's + ig + jg's'

y = x + ix' = (x + ix) + ix' = x + i

Результаты,полученные Порецким :

x = xs

y = g's + gy

y = y + x

Результаты Порецкого менее корректны,поскольку он использует 2-значную(с некоторой натяжкой ее можно считать псевдо-трехзначной: здесь в качестве i выступает символ функции,встречающийся в правой части уравнений) логику вместо 4-значной. Метод Порецкого корректен при общих посылках и общем заключении, но он абсолютно непригоден для частных посылок и частных заключений. Порецкий своими методами мог бы частично обосновать русскую силлогистику[3], в том числе доказать некорректность 1-го модуса 4-й фигуры.