Недостатки и ошибки классической логики Аннотация

В статье анализируются недостатки и грубейшие ошибки классической логики в таких её разделах как логика суждений и логика предикатов. Отмечается недопустимость преподавания логики с подобными изъянами. Предлагаются простые, доступные пониманию школьников, математические методы решения проблем логики, возраст которых превышает 24 века. Впервые в мире решена задача Лейбница о переводе логики на математическую основу. Методы апробированы в течение 6-летноего преподавания в школах и колледжах, при чтении лекций в НПФ "Знание", в докладах на международных конференциях по проблемам логики. Результаты автора изложены в многочисленных отечественных и зарубежных публикациях.

Фундаментом классической логики служат логика суждений и логика предикатов (силлогистика). До сих пор доказательство различных логических законов ведётся на основе громоздких таблиц истинности, что лишний раз свидетельствует о низком профессиональном уровне "классиков". Переход к аналитическим методам доказательства предельно прост, но почему-то никто из "логиков"[1] до него не додумался. Возможно "профессионалов" отпугивает минимизация логических функций. Действительно, если использовать традиционные методы (Квайна, Блека - Порецкого), то проводить аналитическое доказательство не захочется. Поэтому автор ещё в 1977г. разработал алгоритмы для работы с картами Карно, что существенно упростило минимизацию[2, 3]. На основе этих алгоритмов были разработаны новые методы анализа и синтеза законов логики суждений, силлогизмов, соритов, полисиллогизмов и решения логических уравнений[5 - 18, 29]. Начнём с доказательства законов логики суждений и анализа заключений импликативных силлогизмов.

Алгоритм "Импульс".

Алгоритм анализа (доказательства) законов логики суждений чрезвычайно прост (здесь и далее апостроф означает отрицание):

1. произвести замену всех знаков импликации на символы дизъюнкции в соответствии с известной формулой x ® y = x' + y;

2. привести полученное выражение с помощью закона Де Моргана к дизъюнктивной нормальной форме (ДНФ);

3. занести ДНФ в карту Карно и убедиться, что она вся покрыта единицами - это свидетельствует о истинности проверяемого закона или суждения.

Воспользуемся алгоритмом "Импульс" для доказательства наиболее интересных законов логики суждений.

Законы импликативных силлогизмов

1.Если [(если р, то q) и (если р,то r)], то [если р, то(q и r )].

[(p -> q)(p -> r)] -> (p -> qr) = [(p' + q)(p' + r)]' + (p' + qr) =

= (p'+qr)'+p'+qr = 1.

2.Если [(если р, то q) и (если r,то s)],то [если(р и r),то (q и s)].

[(p->q)(r->s)] -> (pr->qs) = [(p'+q)(r'+s)]'+p'+r'+qs =

= pq'+rs'+p'+r'+qs = 1.

3.Если [(если р, то q) и (если q, то r)],то (если р, то r).

[(p->q)(q->r)] -> (p->r) = pq'+qr'+p'+r = 1.

4.Если [(если р, то q) и (если r, то q)],то [если (р или r), то q].

[(p->q)(r->q)] -> [(p+r) ->q] = pq'+rq'+p'r'+q = 1.

Как видит читатель, такие законы можно "изобретать" и доказывать десятками. Во всех выводах применялась аналитическая минимизация логических функций. Однако значительно проще для этой цели использовать карты Карно[2, 3].

Решим аналитически одну из задач Катречко[4, 6].

Задача

Если бог существует, то он всемогущ и всеблаг. Бог или бессилен предотвратить зло, или он не желает предотвращать его( зло существует на Земле). Если бог всемогущ, то неверно, что он бессилен предотвратить зло. Если бог всеблаг, то неверно, что он не желает предотвращать зло. Следовательно, неверно, что бог существует.

Решение

X - бог всемогущ,

Y - бог всеблаг,

Z - бог существует,

U - зло существует,

V - бог бессилен против зла,

W - бог желает предотвратить зло.

(z -> xy)u(u -> (v+w'))(x -> v')(y -> w) -> z' =

= (z'+xy)u(u'+v+w')(x'+v')(y'+w) -> z' =

= z(x'+y')+u'+uv'w+xv+yw'+z' = 1.

Мы строго математически доказали, что вера в бога ошибочна. Это верно при условии, что все наши посылки корректны. Здесь для минимизации логической функции была использована карта Карно от 6 переменных. Аналитический метод минимизации был бы чрезвычайно утомителен и без гарантии успеха, а применение машинной минимизации - неэффективно: "из пушки по воробьям". Полное решение всех задач Катречко можно найти в [6].

Важнейшим разделом классической логики является силлогистика, или логика предикатов. Силлогизм - это умозаключение, в котором из двух посылок, связанных общим термином, выводится заключение. Силлогистика - раздел логики, занимающийся анализом и синтезом силлогизмов. Изучение этого раздела невозможно без решения задач, что вызывает непреодолимые трудности не только у студентов, но и у преподавателей. Ни один академик не умеет решать задачи по силлогистике. О формальных методах анализа и синтеза силлогизмов мечтал самый выдающийся математик всех времён и народов Г.В. Лейбниц: "Единственное средство улучшить наши умозаключения состоит в том, чтобы сделать их столь же наглядными, как и у математиков, - такими, что их ошибочность можно было бы увидеть глазами, и если между людьми возникают разногласия, достаточно было бы только сказать: "Вычислим! " - чтобы без долгих рассуждений стало ясно, кто прав".

Для общеразговорной логики вполне достаточно трёх или даже двух (Axy и Ixy) базовых суждений (силлогистических функторов):

1. Все X суть Y(Axy);

2. Ни один X не есть Y(Exy);

3. Некоторые X суть Y(Ixy);

Для создания истинно математической силлогистики необходимо прежде всего аналитически описать все силлогистические функторы. До сих пор ни в одном учебнике таких формул нет. Поскольку функторы описывают множества, то для их отображения были созданы круги Эйлера, диаграммы Венна и диаграммы Ламберта. Они не решили поставленной задачи. Автору пришлось ввести скалярные диаграммы определённого вида (диаграммы Лобанова) и применить к ним формальный синтез логических функций. Таким образом был построен базис силлогистики[7 - 18]. На приведённых рисунках представлен процесс перехода от диаграмм Венна к диаграммам Лобанова и синтез логических функций для силлогистических функторов Axy, Exy, Ixy.

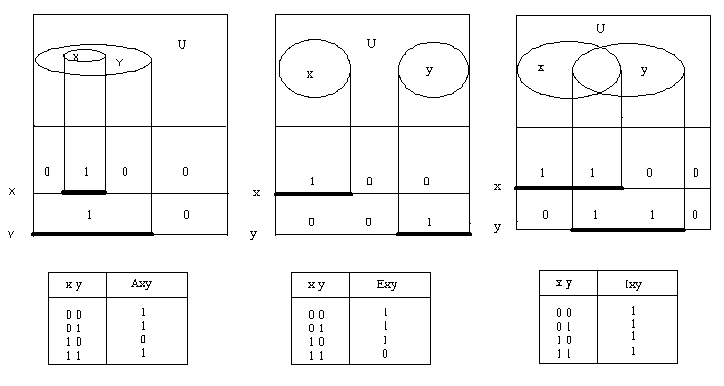
Axy = x' + y Exy = x' + y' Ixy(8) = 1

Под базисом будем понимать определённый набор функторов Аху, Еху, Ixy. В общеразговорной логике все суждения построены в базисе Васильева, поскольку именно он отражает логику здравого смысла(см. вышеприведённый рисунок). Этот базис имеет следующее аналитическое представление:

Axy = x'+y = (xy')'

Exy = x'+y' = (xy)'

Ixy(8) = x+y+x'y' = 1,

где в скобках указан номер базиса для частно-утвердительного суждения. С помощью этого базиса можно представить любой другой базис, заменив скалярные диаграммы. Для фиксации и компактного описания введем операцию сцепления (конкатенации) функторов, обозначив ее символом ||. Тогда для частно-утвердительного функтора могут быть получены следующие описания и аналитические выражения [5 - 12]:

1. Ixy(1) = Axy & Ax'y = x;

2. Ixy(2) = Ixy(8) || (Ax'y & Ay'x) = x+y+ix'y' - русский функтор;

3. Ixy(3) = Ixy(8) || (Ax'y & Ay'x) || Axy || Ayx = xy + i(x'+y') - функтор Аристотеля;

4. Ixy(4) = Ixy(8) || Ayx = x+y'+ ix'y;

5. Ixy(5) = Ixy(8) || Ayx || (Ax'y & Ay'x) = x+ix';

6. Ixy(6) = (Ax'y & Ay'x) = x+y;

7. Ixy(7) = Ixy(8) || Axy || (Ax'y & Ay'x) = y+iy';

8. Ixy(8) = x+y+x'y' = 1 - функтор Васильева.

Автором разработаны несколько алгоритмов анализа и синтеза силлогизмов[7 - 18]. Здесь приводится лишь наиболее простой и наглядный алгоритм ТВАТ.