
- •Варианты типового расчёта Вариант 1.
- •4. Найти площадь фигуры, ограниченной линиями , .
- •Вариант 2.
- •2. Найти площадь фигуры, ограниченной линиями ; .
- •Вариант 3.
- •5. Найти длину дуги кривой , .
- •6. Найти длину дуги кривой, заданной в параметрическом виде , .
- •7. Оценить интеграл, не вычисляя его .
- •Вариант 4.
- •Вариант 5.
- •5. Найти длину дуги кривой , .
- •6. Найти длину дуги кривой, заданной в параметрическом виде , .
- •7. Оценить интеграл, не вычисляя его .
- •Вариант 6.
- •5. Найти длину дуги кривой , .
- •Вариант 7.
- •Вариант 8.
- •4. Найти площадь фигуры, ограниченной линиями , .
- •5. Найти длину дуги кривой , .
- •Вариант 9.
- •3. Найти площадь фигуры в полярной системе координат.
- •5. Найти длину дуги кривой , .
- •Вариант 10.
- •4. Найти площадь фигуры, ограниченной линиями , .
- •5. Найти длину дуги кривой , .
- •6. Найти длину дуги кривой , .
- •Вариант 11.
- •7. Вычислить среднее значение функции на отрезке .
- •Вариант 12.
- •Вариант 13.
- •8. Оценить интеграл .
- •Вариант 14.
- •4. Вычислить площадь фигуры, ограниченной кривой .
- •7. Оценить интеграл .
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •7. Вычислить среднее значение функции на отрезке
- •Вариант 19.
- •2. Вычислить площадь фигуры, ограниченной линиями и .
- •7. Оценить интеграл, не вычисляя его .
- •Вариант 20.
- •6. Найти длину дуги кривой , .
- •Вариант 21.
- •6. Найти длину дуги кривой , .
- •Вариант 22.
- •Вариант 23.
- •Вариант 24.
- •Вариант 25.
- •2. Вычислить площадь фигуры, ограниченной линиями и .
- •Вариант 26.
- •Вариант 27.
- •Вариант 28.
- •3. Вычислить площадь фигуры, ограниченной кривой .
- •5. Найти длину дуги кривой .
- •Вариант 29.
- •Вариант 30.
- •Вариант 31.
- •3. Вычислить площадь фигуры, ограниченной кривой .
- •Вариант 32.
Вариант 21.
1.
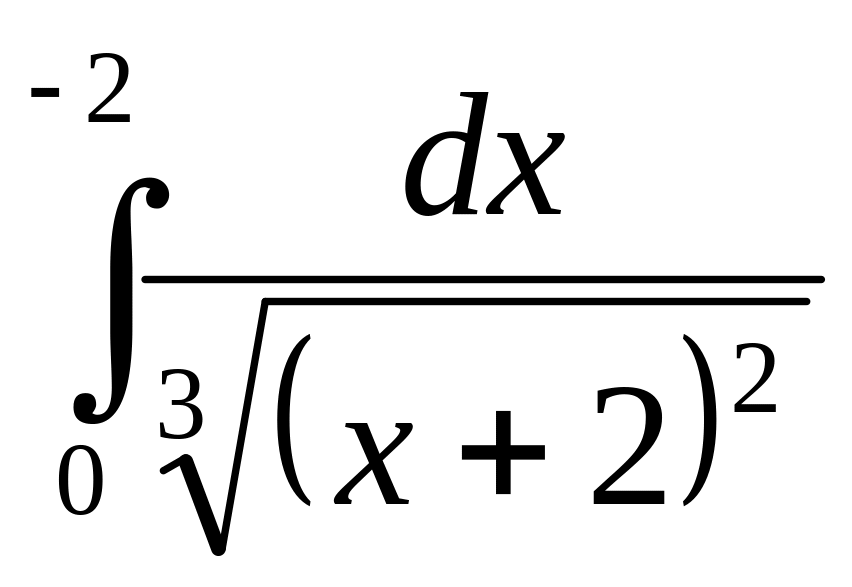 ,
,
![]() ,
,
![]() ,
,
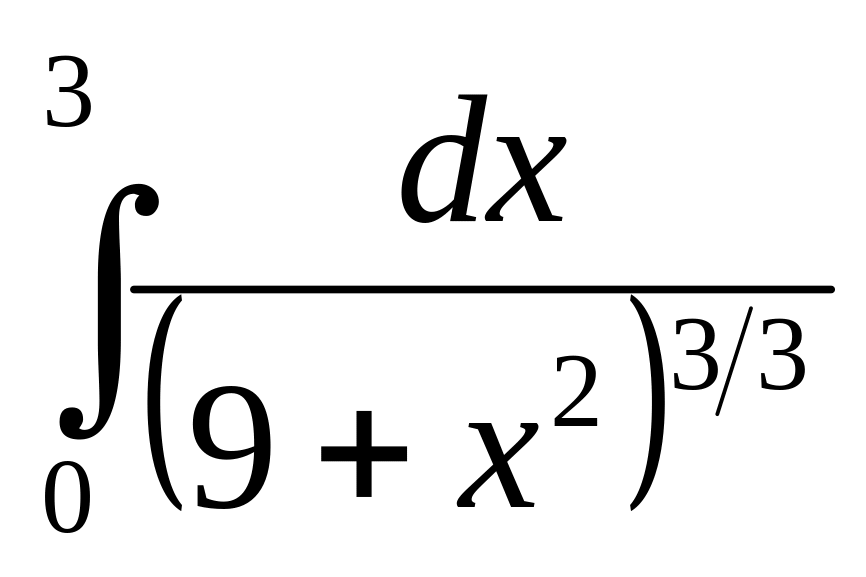 .
.
2. Вычислить площадь фигуры, ограниченной
линиями
,
![]() ,
.
,
.
3. Вычислить площадь фигуры, ограниченной
линией
![]() .
.
4. Вычислить площадь фигуры, ограниченной
линиями
![]() ,
,
![]() .
.
5. Вычислить длину дуги кривой
![]()
![]() .
.
6. Найти длину дуги кривой , .
7. Оценить интеграл![]() ,
не вычисляя его.
,
не вычисляя его.
8. Определить объем тела вращения фигуры,
образованной линиями
![]() ,
,
![]() вокруг оси OX.
вокруг оси OX.
9. Скорость движения тела пропорциональна кубу времени. В конце 8-й секунды скорость тела равна 5м/с. Чему равен путь, пройденный телом за 5с.?
Вариант 22.
1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Определить площадь фигуры, ограниченной
линиями
![]() ,
,
![]() ,
.
,
.
3. Вычислить общую часть площади, ограниченную линиями в полярной системе координат , .
4. Вычислить площадь фигуры
,
![]() .
.
5. Вычислить длину дуги кривой
![]() .
.
6. Вычислить длину дуги кривой
![]() ,
,
![]() .
.
7. Доказать, что
![]() .
.
8. Найти объем тела, образованного
вращением фигуры, ограниченной линиями
![]() и
вокруг оси OY.
и
вокруг оси OY.
9. Определить давление воды на вертикальный параболический сегмент, основание которого равно 4м и расположено на поверхности воды, а вершина лежит на глубине 4м.
Вариант 23.
1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Вычислить площадь фигуры, ограниченной
линиями
![]() ,
,
![]() .
.
3. Вычислить общую часть площади,
ограниченную линиями в полярной системе
координат
![]() .
.
4. Вычислить площадь фигуры, ограниченной
линиями
![]() ,
.
,
.
5. Вычислить длину дуги кривой
![]() ,
.
,
.
6. Вычислить длину дуги кривой
![]() .
.
7. Доказать, что
![]() .
.
8. Найти объем тела вращения, если вокруг
оси OY вращается фигура,
ограниченная линиями
![]() ,
.
,
.
9. Вычислить силу давления воды на вертикальную стенку, имеющую форму трапеции,
нижнее основание которой
![]() ,
верхнее
,
верхнее
![]() и высота
и высота
![]() ,
если уровень погружения нижнего основания
,
если уровень погружения нижнего основания
![]() .
.
Вариант 24.
1.
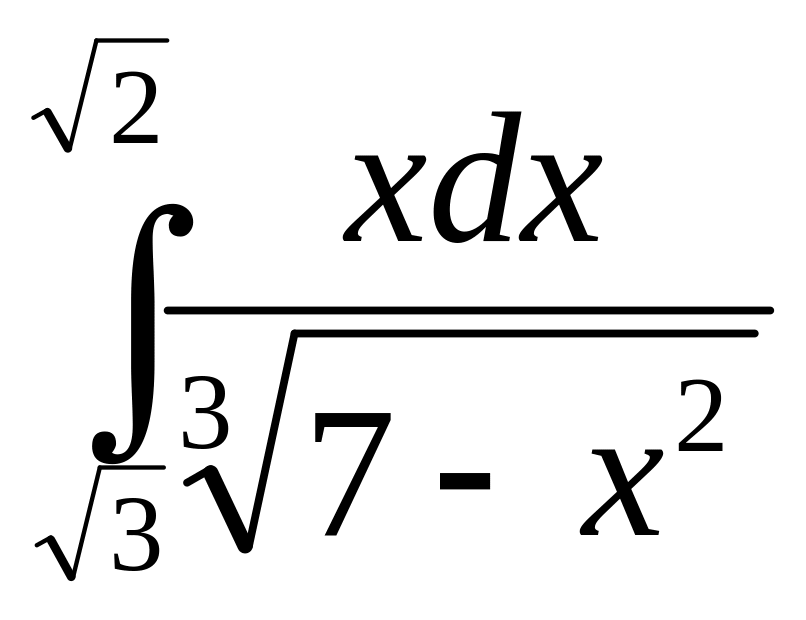 ,
,
![]() ,
,![]() ,
,
![]() .
.
2. Найти площадь фигуры, между линией
![]() и ее асимптотой.
и ее асимптотой.
3. Вычислить площадь фигуры, ограниченной
линией
![]() .
.
4. Вычислить площадь фигуры, ограниченной
линиями
![]() ,
,
![]() .
.
5. Вычислить длину дуги линии
![]() ,
отсеченной прямой
.
,
отсеченной прямой
.
6. Вычислить длину дуги кривой, заданной уравнениями .
7. Оценить интеграл , не вычисляя его.
8. Вычислить объем тела вращения,
образованного вращением фигуры,
образованной кривыми
и
![]() около оси OX.
около оси OX.
9. Какую работу надо затратить, чтобы тело массой m поднять с поверхности земли на высоту h? Чему равна эта работа, если тело должно быть удалено в бесконечность?
Вариант 25.
1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Вычислить площадь фигуры, ограниченной линиями и .
3. Вычислить общую часть площади,
ограниченную линиями в полярной системе
координат
![]() .
.
4. Вычислить площадь фигуры, ограниченной
линиями
![]() ,
,
![]() .
.
5. Вычислить длину дуги кривой
![]() ,
отсеченной прямой
,
отсеченной прямой
![]() .
.
6. Вычислить длину дуги параметрической кривой .
7. Оценить интеграл![]() ,
не вычисляя его.
,
не вычисляя его.
8. Вычислить объем тела вращения,
образованного дугой кривой
![]() при ее вращении вокруг оси OY
от
при ее вращении вокруг оси OY
от
![]() до
до
![]() .
.
9. Вычислить кинетическую энергию диска
массы M и радиуса R,
вращающегося с угловой скоростью
![]() около оси, проходящей через его центр,
перпендикулярно его плоскости.
около оси, проходящей через его центр,
перпендикулярно его плоскости.
