Задание №2
Найти производные
данных функций
.
а)
б)
Решение
а)
Используя формулы
,
,
,
где
-
сложная функция, получим
.
.
б) . Заменим кубический корень дробным показателем и найдем производную сложной степенной функции (формулы и , где - сложная функция):
,
.
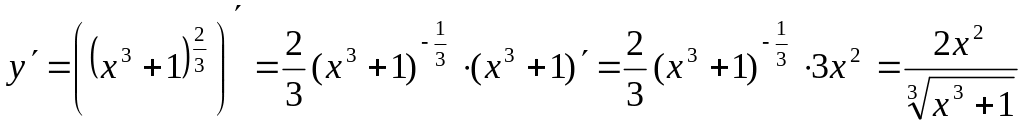Задание №3
Исследовать методами дифференциального исчисления функцию и построить ее график, используя результаты исследования.
.
Решение
Находим область определения функции:
.
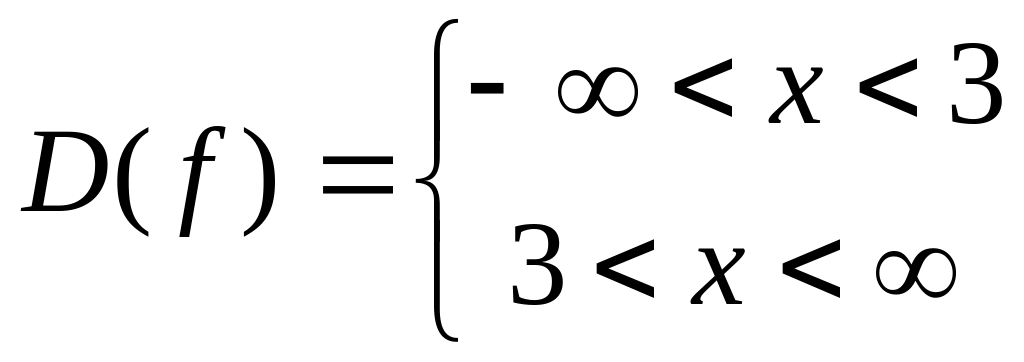Данная функция не является ни четной, ни нечетной, ни периодической, так как ее область определения не симметрична относительно начала координат.
При
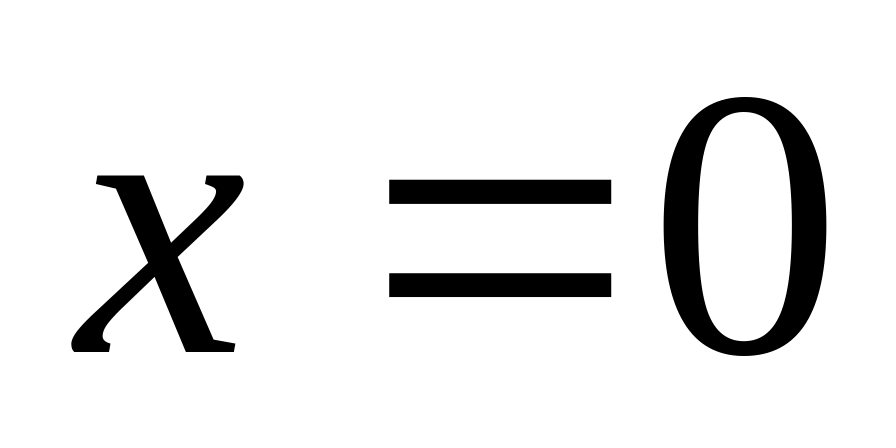получим
,
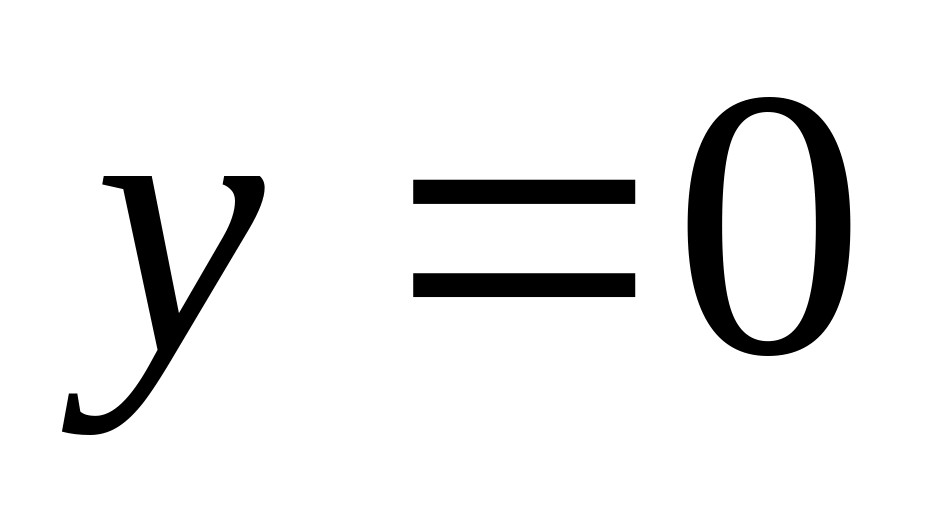т.е. график проходит через начало
координат.
Так как
,
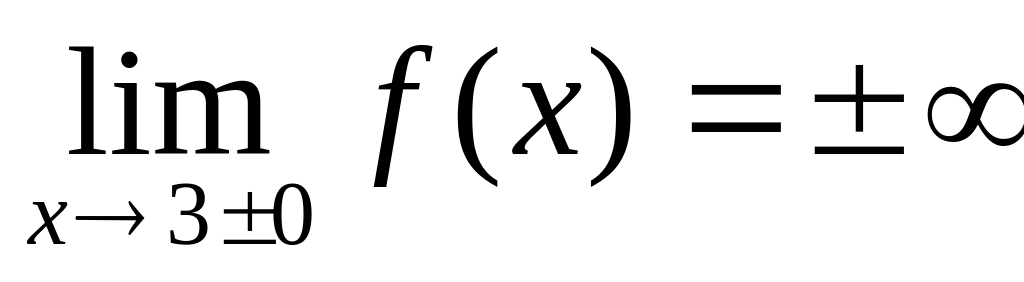то прямая
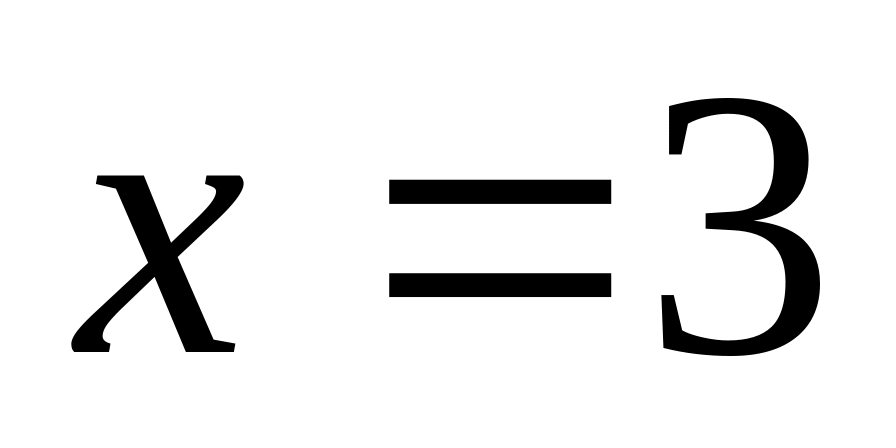служит
вертикальной асимптотой графика. Далее
находим:
,
.
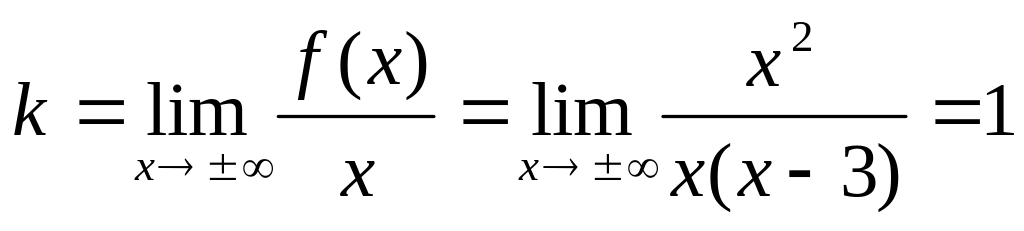Следовательно,
прямая
является
наклонной асимптотой графика.
Находим
.
Производная
обращается
в нуль в точках
и
и терпит разрыв при
.
Этими точками числовая прямая делится
на четыре промежутка:
,
,
,
.
Исследуем знак производной
в
каждом из них; очевидно, что
в
промежутках
и
(в
этих промежутках функция возрастает)
и
в
промежутках
и
(в этих промежутках функция убывает).
При переходе через точку
производная
меняет знак с плюса на минус, т.е. это
точка максимума, а при переходе через
точку
производная
меняет знак с минуса на плюс, т.е. это
точка минимума. Находим
,
.
Находим
.
Вторая производная
в нуль нигде не обращается и терпит
разрыв при
.
В промежутке
имеем
,
т.е. в этом промежутке кривая выпукла
вверх; в промежутке
имеем
,
т.е. в том промежутке кривая выпукла
вниз. Точек перегиба нет.
На основании полученных данных построим график функции.
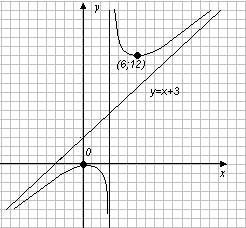
Задание №4
Найти неопределенный интеграл
а)
б)
в)
Решение
а) .
Так как
,
то
.
б) .
Введем подстановку
.
Дифференцируя, имеем
,
откуда
.
Подставив в данный интеграл вместо
и
их выражения, получим
.
Заменив
его
выражением через
,
находим
.
в) .
Положим
,
;
тогда
,
,
т.е.
.
Используя формулу
,
получим
.
Задание №5
Вычислить определенный интеграл
Решение
Положим
;
тогда
,
.
Вычисляем новые пределы интегрирования:
,
.
Потому
.
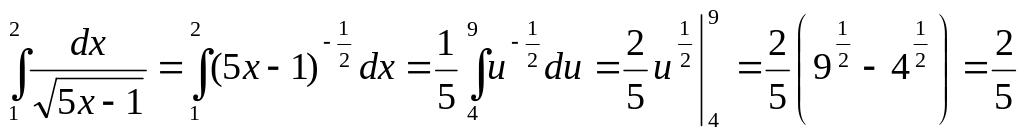Задание №6
Вычислить площадь фигуры, ограниченной линиями
и
.
Решение
Выполним построение фигуры:
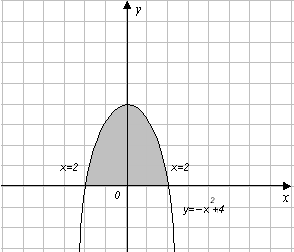
Искомая площадь
заключена между параболой
и
осью
.
Найдем точки
пересечения параболы с осью
.
Полагая
,
найдем
.
Так как данная фигура симметрична
относительно оси
,
то вычислим площадь фигуры, расположенной
справа от оси
,
и полученный результат удвоим:
(кв.
ед.).
(кв. ед.).
Задание №7
Найти частный интеграл (решение) дифференциального уравнения, удовлетворяющий заданным начальным условиям
,
,
.
Решение
Так как характеристическое
уравнение
имеет
равные действительные корни
,
то общее решение данного дифференциального
уравнения записывается в виде
.
Дифференцируя общее решение, имеем
.
Подставив начальные
данные в выражения для
и
,
получим систему уравнений
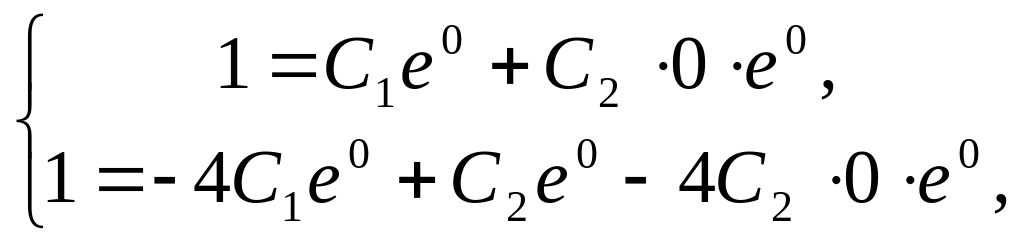или
откуда
и
.
Следовательно, искомое частное решение
имеет вид
.