
- •Программа государственного экзамена для специальности 010101.65 «Математика»
- •Алгебра и геометрия
- •Математический анализ
- •Теория функций комплексной переменной
- •Топология и функциональный анализ
- •Дифференциальные уравнения
- •Теория вероятностей
- •Задания, включенные в программу государственного квалификационного экзамена Раздел «Функциональный анализ и топология»
- •Раздел “Математический анализ”
- •Раздел “Теория функций комплексного переменного”
- •I. Действия над комплексными числами
- •II. Функции комплексного переменного. Понятие голоморфности
- •III. Свойства голоморфных функций. Теорема Коши. Интегральная формула Коши
- •IV. Особые точки. Теория вычетов
- •Раздел «Уравнения с частными производными»
- •Раздел «Теория групп»
- •Раздел «Дифференциальные уравнения»
- •Раздел «Методы оптимизации»
- •Литература
IV. Особые точки. Теория вычетов
15. Определить изолированные особые точки функции f(z), выяснить их характер, написать разложение в ряд Лорана в окрестности этих точек:
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() .
.
16. Используя теорию вычетов, найдите интеграл:
а)
![]() б)
б)
![]() в)
в) .
.
Раздел «Уравнения с частными производными»
1. Решить задачу

2. Решить задачу

3. Решить задачу

4. Решить задачу

5. Решить задачу

Раздел «Аналитическая геометрия»
Составить канонические уравнения прямой, проходящей через точку
 параллельно плоскости
параллельно плоскости
 и образующей угол
и образующей угол
 с прямой
с прямой
 .
.
(Ответ
![]() )
)
Определить тип кривой и построить эту кривую в системе координат :
 (Ответ эллипс)
(Ответ эллипс)
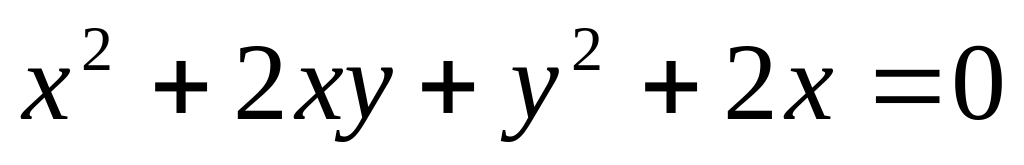 (Ответ парабола)
(Ответ парабола) (Ответ гипербола)
(Ответ гипербола)
Вычислите расстояние между параллельными сторонами параллелограмма, построенного на векторах
 .
Ответ (
.
Ответ ( )
)Найдите высоту тетраэдра ABCD, опущенного из вершины B, зная, что
 Ответ (
Ответ (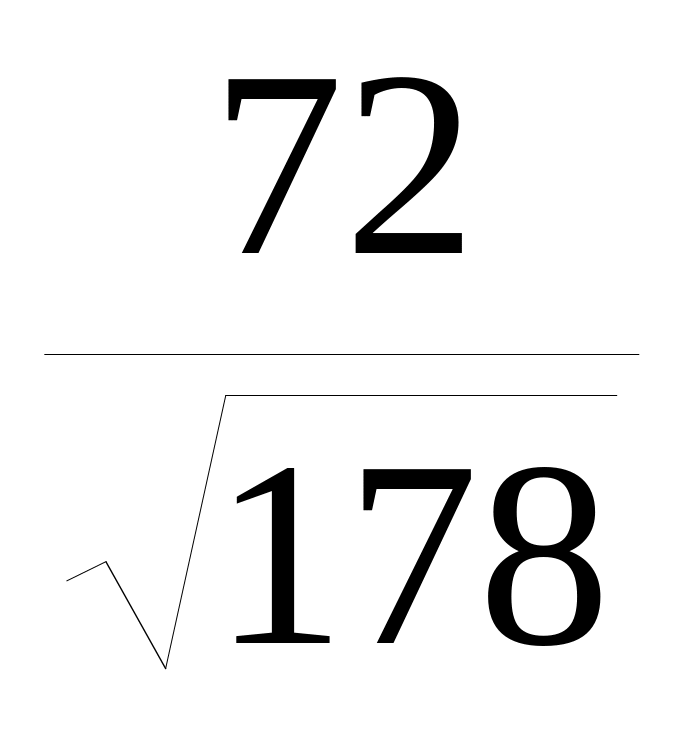 )
)
Даны два вектора
 .
Найдите единичный вектор
.
Найдите единичный вектор
 ,
ортогональный векторам
,
ортогональный векторам
 и
и
 и направленный так, чтобы упорядоченная
тройка векторов
,
,
была правой. (Ответ
и направленный так, чтобы упорядоченная
тройка векторов
,
,
была правой. (Ответ
 .
.
Раздел «Алгебра и геометрия»
Разложите многочлены на неприводимые над R и C:
![]() .
.
.Найдите размерность линейной оболочки векторов
 :
При каких
:
При каких указанные
векторы образуют базис в R4
?
указанные
векторы образуют базис в R4
?Найдите матрицу оператора дифференцирования в пространстве
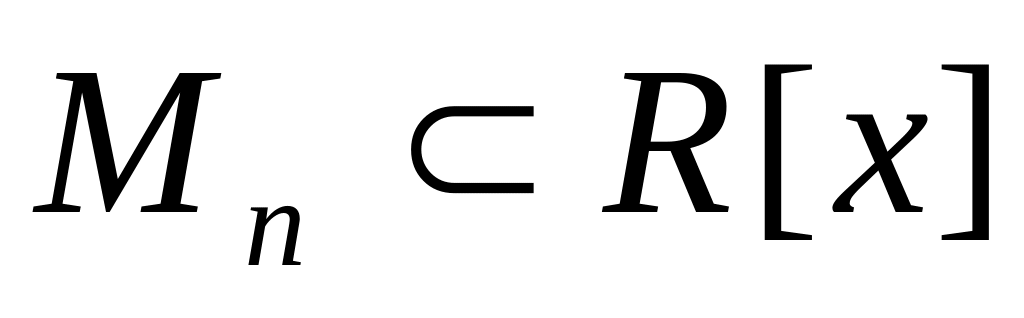 полиномов степени не выше n
в базисе
полиномов степени не выше n
в базисе
 .
.
Найдите ортонормированный базис из собственных векторов и матрицу в этом базисе для линейного оператора , заданного в некотором базисе матрицей
 .
.
Раздел «Теория групп»
Пусть
 -
группа ненулевых комплексных чисел с
операцией умножения. Доказать, что
множество корней степени 6 из единицы
является циклической подгруппой группы
-
группа ненулевых комплексных чисел с
операцией умножения. Доказать, что
множество корней степени 6 из единицы
является циклической подгруппой группы
 и найти все образующие этой подгруппы.
и найти все образующие этой подгруппы.
Доказать, что множество
 является
подгруппой группы
является
подгруппой группы
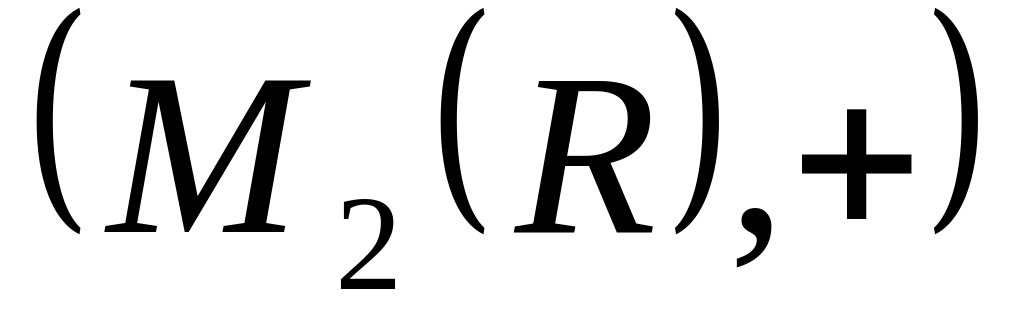 всех вещественных квадратных матриц
с операцией сложения. Пусть
всех вещественных квадратных матриц
с операцией сложения. Пусть
 –
отображение, заданное формулой
–
отображение, заданное формулой
 .
Являются ли отображения
.
Являются ли отображения
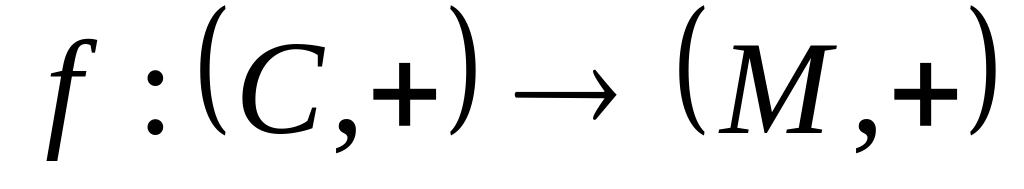 и
и
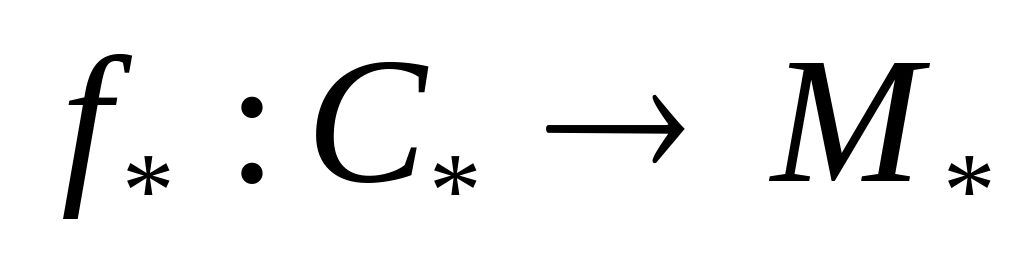 ,
где
,
,
где
,
 и
и
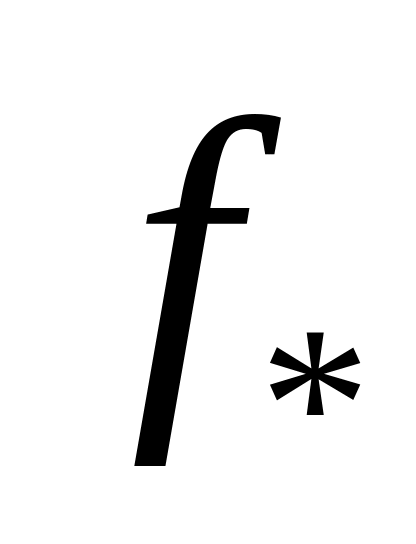 –
ограничение отображения
–
ограничение отображения
 ?
?
Раздел «Топология»
1. Докажите, что связное компактное множество на прямой является отрезком.
Раздел «Теория вероятностей»
В каждой из трех урн находится по 6 белых и 4 черных шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым
Равнобедренный треугольник образован единичным вектором в направлении оси абсцисс и единичным вектором в случайном направлении в пространстве
 .
Найдите функцию распределения третьей
стороны.
.
Найдите функцию распределения третьей
стороны.
Пусть
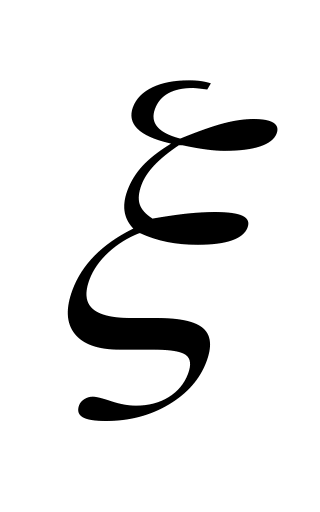 и
и
 –
случайные величины,
–
случайные величины,
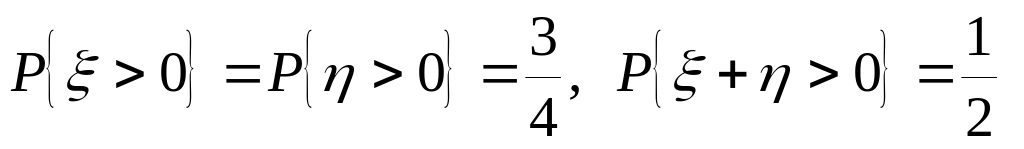 .
Доказать, что
и
– зависимые случайные величины
.
Доказать, что
и
– зависимые случайные величины
Написаны n писем, предназначенных разным адресатам. Имеется n конвертов с соответствующими адресами. Письма в случайном порядке вкладываются в конверты. Пусть
 –
число писем, посланных тем адресатам,
которым они предназначены. Найти
математическое ожидание
–
число писем, посланных тем адресатам,
которым они предназначены. Найти
математическое ожидание
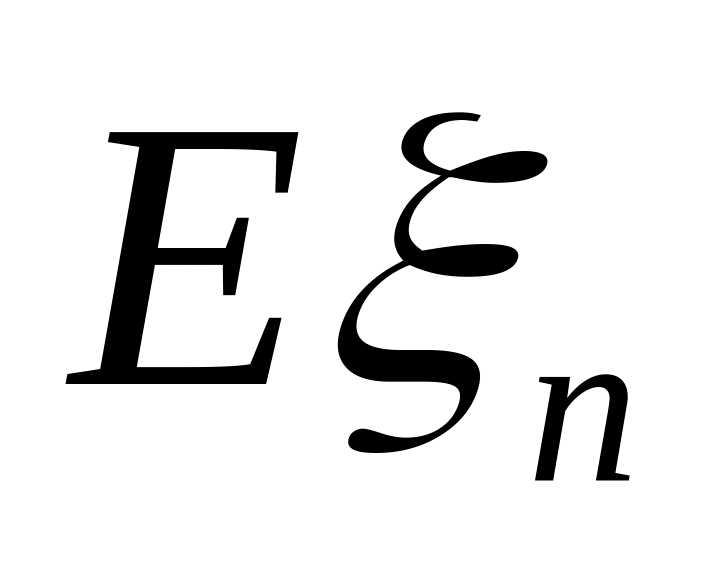 .
.Две точки выбираются наудачу из отрезка [0, 1]. Пусть p и q – координаты этих точек. Найдите вероятность того, что квадратное уравнение
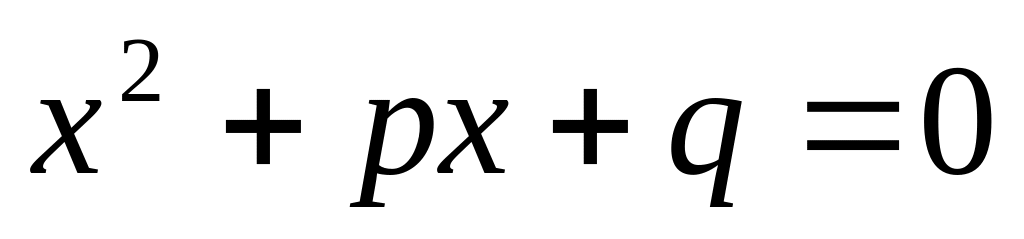 будет иметь вещественные корни.
будет иметь вещественные корни.Стержень ломается случайным образом на две части. Каково среднее отношение длины короткого куска к длине длинного куска?
