
- •Программа государственного экзамена для специальности 010101.65 «Математика»
- •Алгебра и геометрия
- •Математический анализ
- •Теория функций комплексной переменной
- •Топология и функциональный анализ
- •Дифференциальные уравнения
- •Теория вероятностей
- •Задания, включенные в программу государственного квалификационного экзамена Раздел «Функциональный анализ и топология»
- •Раздел “Математический анализ”
- •Раздел “Теория функций комплексного переменного”
- •I. Действия над комплексными числами
- •II. Функции комплексного переменного. Понятие голоморфности
- •III. Свойства голоморфных функций. Теорема Коши. Интегральная формула Коши
- •IV. Особые точки. Теория вычетов
- •Раздел «Уравнения с частными производными»
- •Раздел «Теория групп»
- •Раздел «Дифференциальные уравнения»
- •Раздел «Методы оптимизации»
- •Литература
Раздел “Математический анализ”
Докажите, что если
 сходится, то в ней есть или наибольший
член, или наименьший, или тот и другой.
сходится, то в ней есть или наибольший
член, или наименьший, или тот и другой.Докажите, что если
 ,
то среди ее членов есть наименьший.
,
то среди ее членов есть наименьший.Докажите, что для сходимости монотонной последовательности достаточно сходимости некоторой ее подпоследовательности.
Найти
 ,
если: а)
,
если: а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.Найти суммы рядов: а)
 ;
б)
;
б)
 .
.Найти пределы: а)
 (
( );
б)
);
б)
 ;
в)
;
в)
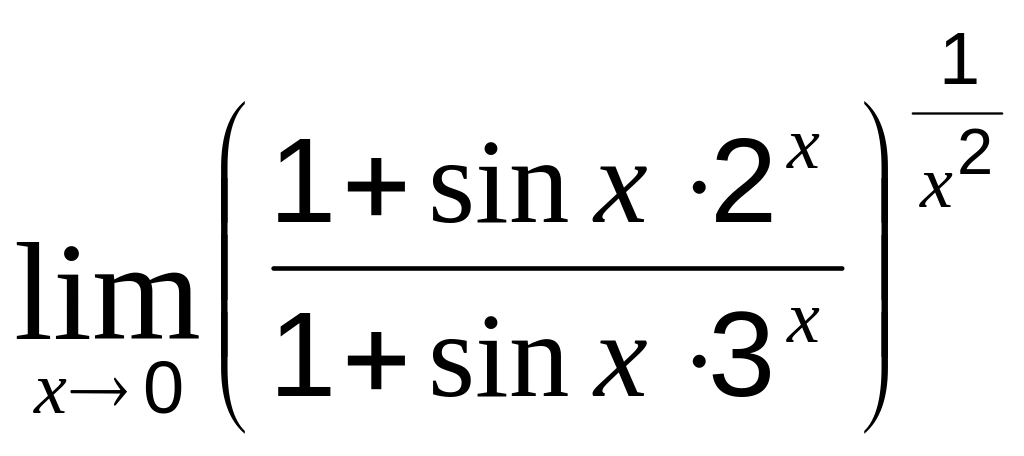 ;
г)
;
г)
 .
.Найти интегралы: а)
 ;
б)
;
б)
 ;
в)
;
в)
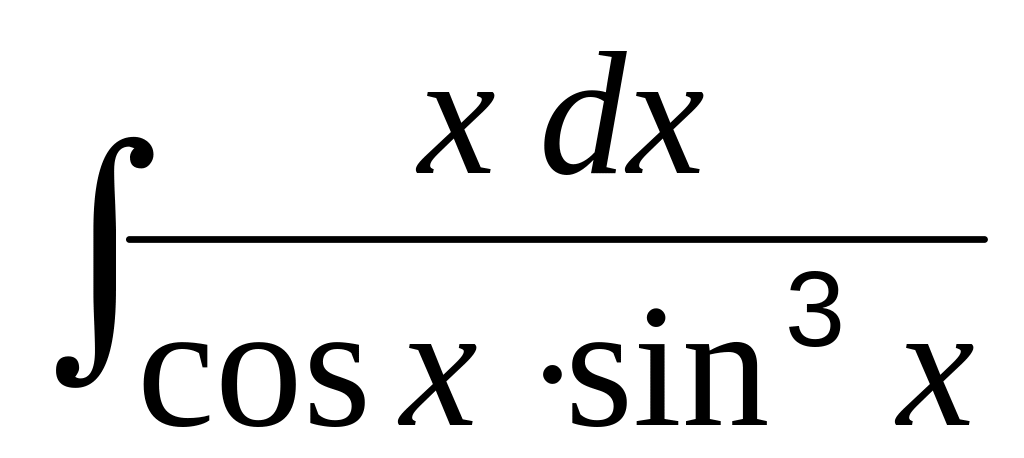 ;
г)
;
г)
 ;
д)
;
д)
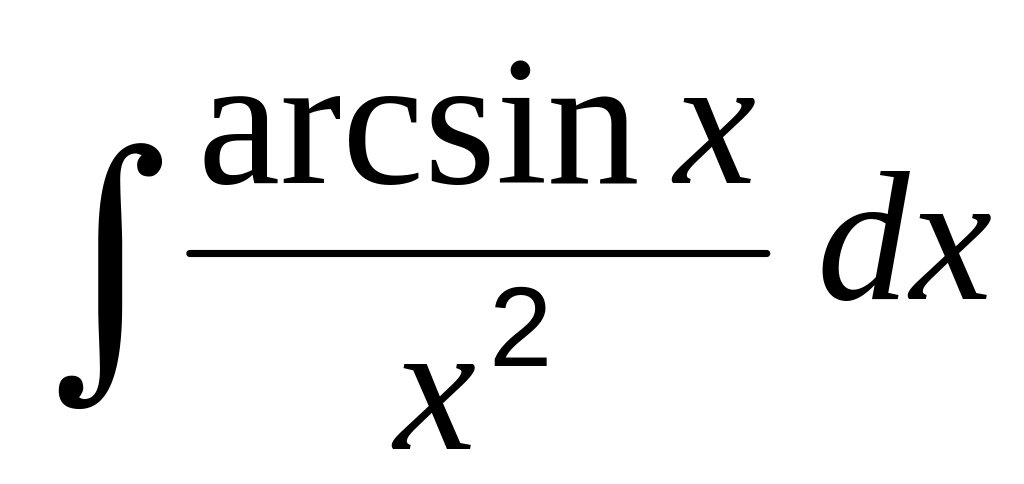 .
.Найти площадь фигуры, ограниченной кривой: а)
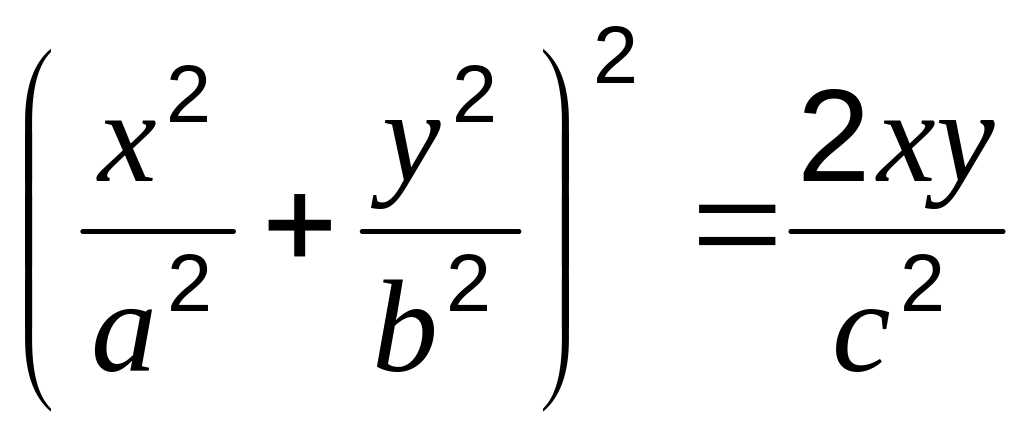 ;
б)
;
б)
 .
.Вычислить объем тела, ограниченного поверхностью: а)
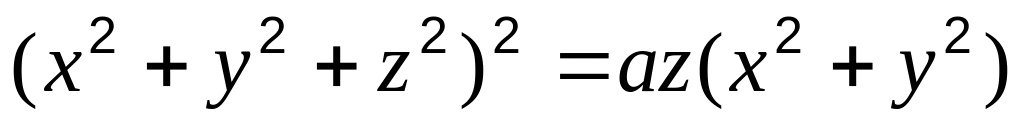 ;
б)
;
б)
 .
.Вычислить интегралы: а)
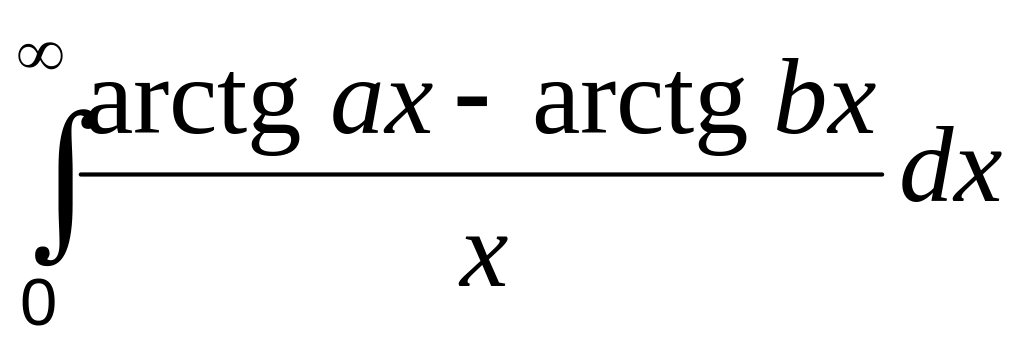 (
(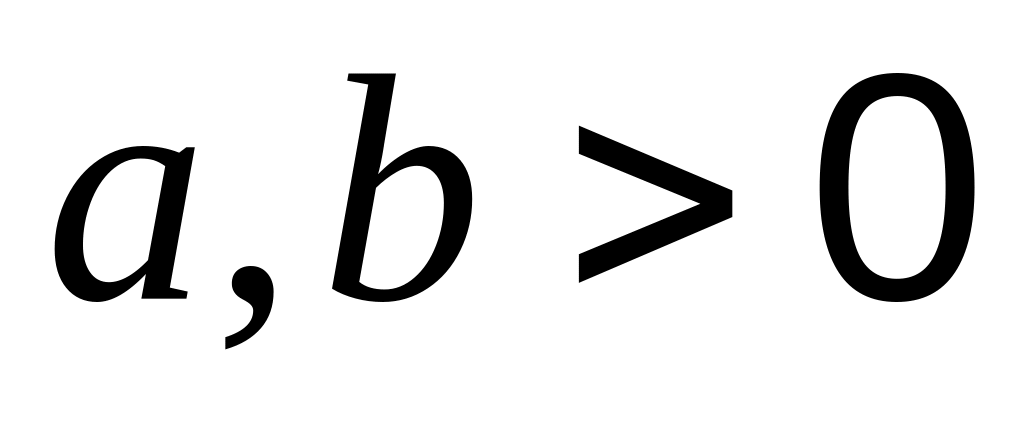 );
б)
);
б)
 (
);
в)
(
);
в)
 ;
г)
;
г)
 .
.Исследовать на сходимость числовые ряды: а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.Исследовать на экстремум следующие функции многих переменных: а)
 ,
,
 ;
б)
;
б)
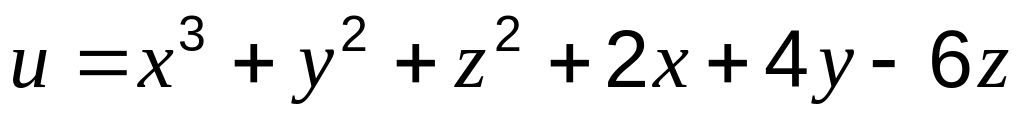 ;
в)
;
в)
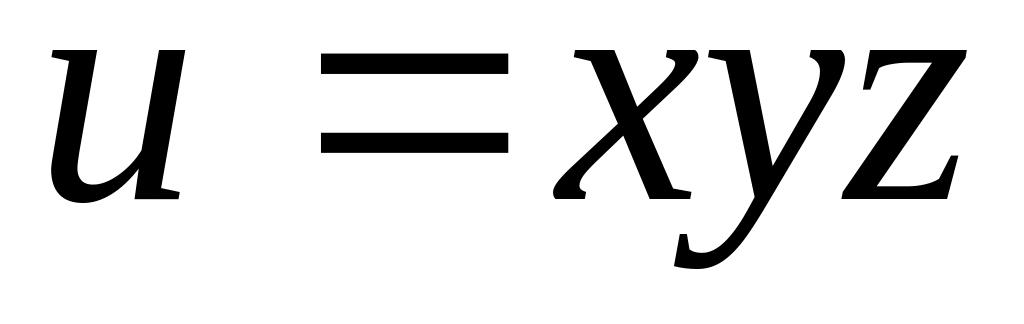 ,
если
,
если
 ,
,
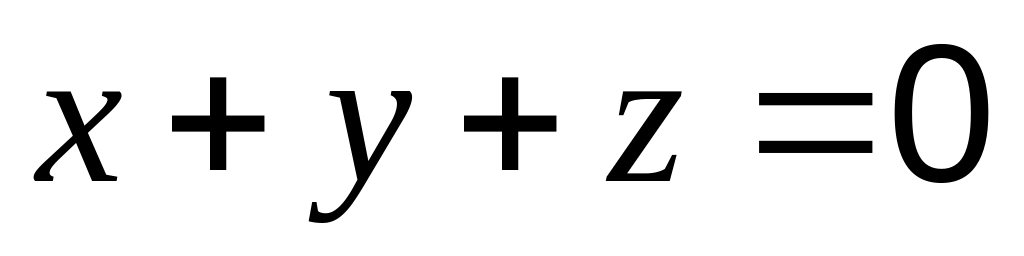 .
.
Раздел “Теория функций комплексного переменного”
I. Действия над комплексными числами
Найти аргумент и модуль комплексного числа:


 a)
a)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)*
д)*
![]()
Найти все значения nN , для которых
 ,
где i-
мнимая единица.
,
где i-
мнимая единица.В плоскости комплексного переменного
 нарисовать множество точек z ,
удовлетворяющих условию
нарисовать множество точек z ,
удовлетворяющих условию
а)
![]() б)
б)
![]() в)
в)
![]()
г)![]()
II. Функции комплексного переменного. Понятие голоморфности
4. Выяснить, голоморфны ли функции
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
5. Проверить выполнение условий Коши-Римана для функций:
а)
![]() б)
б)
![]() в)
в)
![]()
6. Найти образ
полуплоскости {zC:
Im z>0} при отображении
![]() .
.
7. Найти образ
окружности {z:
![]() }
при отображении
}
при отображении
![]() .
.
8*. Найти образ треугольника с вершинами в точках 0; 1; i при отображении
.
9. Выделите ветви многозначной функции
а)
![]() б)
б)
![]() в)*
в)*
![]()
Отметьте точки ветвления.
10. Вычислите:
а)
![]() б)
б)
![]() в)
в)
![]() г)*
г)*
![]()
III. Свойства голоморфных функций. Теорема Коши. Интегральная формула Коши
11. Используя интегральную формулу Коши вычислите интеграл:
а)
![]() б)
б)
в)
![]() г)
г)
![]() д)
д)
 .
.
12*. Сформулируйте принцип максимума модуля для голоморфной функции,
рассмотрите
пример
![]() .
.
13. Поясните , почему
функция
![]() обращающаяся в нуль на бес-
обращающаяся в нуль на бес-
конечности
множестве E={![]() }
не равна 0 тождественно.
}
не равна 0 тождественно.
Какой пункт теоремы единственности не выполнен ?
14. Используя теорему Лиувилля, докажите основную теорему алгебры.
