8.Термодинамічні потенціали для систем зі змінною кількістю частинок. Хім. Потенціал.

Запишемо основне рівняння термодинаміки для системи, що складається з рідини та газу.

Якщо задана кількість часток пару та рідини, то виникає додаткова робота (крім PdV).

Це потенціали для системи зі змінною кількістю частинок.

V,S – екстенсивні потенціали(можуть бути віднесені к одній частинці), T,P – інтенсивні.

Хімічний потенціал – це є енергія Гібса на одну частинку.

Він є інтенсивним параметром.

Треба ввести потенціал, який би дав можливість знайти кількість частинок N. Він має залежність від

9. Загальні умови рівноваги і стійкості

Будемо виходити з основного співвідношення т. д-ки для нестатичних процесів (об’єднує 1-ше і 2-ге начала для нестаціонарних процесів).

(1)

умови рівноваги і стійкості будемо знаходити для конкретних умов

Ізольована система

1)

процеси самі ідуть в бік збільшення S

в стані рівноваги S максимальне. Умова максимуму в варіаціях (віртуальних змінних):

нехай система знаходиться в рівновазі з термостатом, не змінює V i N :

2)

вільна енергія зменшується і в стані рівноваги мінімальна

умова мінімуму на варіаційній мові:

3)

аналогічно і для інших процесів. Всі потенціали в стані рівноваги мінімальні:

умова, коли перша варіація =0, дає умову рівноваги. Коли 2-га вар-я >0 дає мову стійкості (не для ізольованої системи).

11. Умови стійкості однорідної системи. Детермінанти і коефіцієнти стійкості.

У стані рівноваги потенціали мінімальні, і це пов'язано з тим, що . Будемо казати, що S, V I U мають т.з. будь-які віртуальні зміни δS, δV, δU.

Якщо в системі з'явилися такі зміни, то нам необх. знайти такі умови, щоб система завдовольняла флюктуаціям повернулась в попередній стан.

— диференціал U.

— друга варіація U. Перша варіація дає умову рівноваги, друга — стійкої рівноваги. Вираз δ²U – квадратична форма: .

Умови невід'ємності КФ полягають у тому, що визначник цієї форми і всі його головні мінори позитивні.

,

.

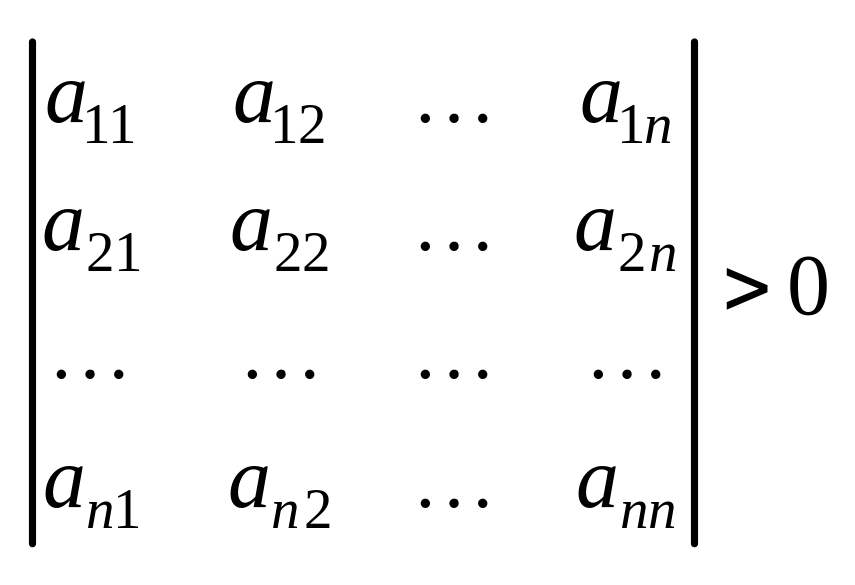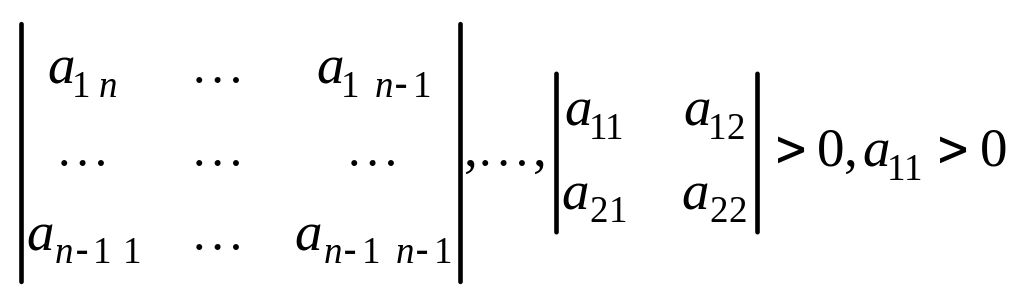Це т.з. Критерій Сільвестра.

— адіабатні коефіцієнти стійкості

Ця матриця дорівнює якобіану D – детермінант Сільвестра.

Якщо є функції , то визначник символічно записується як

і зветься Якобіаном. Властивості Якобіана: 1) будь-яку похідну можна записати як ; 2) ; 3) — обернений Якобіан. Теорія якобіанів використовується при переході від одних змінних до інших; 4) .

Назвемо Якобіан коефіцієнтом стійкості. Для того, щоб система була у стані термодинамічної рівноваги, необхідно щоб D, який являє собою якобіан, збудований з похідних сил по відповідним координатам і всі його головні мінори були позитивні. Величини на головній діагоналі

і назвемо адіабатними коефіцієнтами стійкості (АКС).

— коефіцієнт Гука (шв. звука). Обернена величина — стисливість.

— адіабатне поширення.

Всі похідні в ΔС беруться по термодинамічних координатах. Кожній координаті відповідає термодинамічна сила. V, S = const => ідуть ізохорні адіабатні процеси. Практично легше підтримати const P i T (сталі сили). Перейдемо від похідних по координатах до похідних по силах. Використаємо третю властивість і побудуємо зворотн. ΔС.

, — обернені коефіцієнти стійкості . Це ізодинамічні величини при сталих силах, а величини , назвемо ізодинамічними коефіцієнтами стійкості(ІКС). За стійкості системи відповідають: D, АКС, ІКС, а не будь-які величини. Перш ніж дослідити будь-які системи, необхідно впевнитись, що вона стійка.

_{Знайдемо відповідність між ІКС та АКС.}

. Перейдемо від величини до Якобіану (детермінанту). Робимо роздвижку , де — адіабатний термічний коефіцієнт стійкості.

— ізодинамічний термічний коефіцієнт стійкості.

Розглянемо АКС:

,

.

Це рівняння пов'язує ΔС з КС.

КС мають прозорий статичний зміст. Вони обернено пропорційні флуктуаціям системи.