1. Постулати термодинаміки, їх значення для обґрунтування термодинаміки.

Тд-ка вивчає стан системи у рівновазі і при малому відхиленні від рівноваги, тобто нерівноважні процеси не вивчаються. Тд. рівновага означає, що:

1) Всі вел-ни на залежать від часу;

2) Люба система самостійно не вийде із стану рівноваги.

Якщо ці дві умови виконуються, то система знаходиться у рівновазі. Тд-ка базується на трьох постулатах і трьох началах.

Постулат 1

Люба ізольована система обов’язково прийде у стан тд. рівноваги. Цей стан буде називатися середнім значенням системи.

Постулат 2

Стан системи визначається сукупністю зовн. параметрів і темп-р.

Цей постулат вперше вводить темп-ру.

Постулат 3.

Енергія усієї (макроскопічної) системи складається із суми енергій її мікроскоп. частин.

Темп-ра – це інтенсивний параметр. Тд-ка розглядає внутр. енергію, яка складається з енергії всіх взаємодій між частинками, енергії в полі, рівнів енергії. Внутр. енергія є ф-цією стану системи:

Таким чином зміна при зміні стану не залежить від шляху зміни стану. Зміна відбувається у формі роботи і формі тепла. Якщо зміна відбулася при зміні зовн. параметрів, то маємо роботу, а якщо без зміни зовн. параметрів – то теплоту. І робота, і теплота є формами зміни енергії, але енергією вони не являються. Робота і теплоті є ф-ціями процесу. Робота при ізохорному процесі одня, а при ізобарному – інша. Робота, теплота і енергія пов’язані між собою 1 началом тд-ки. Взаємодія між формами зміни енергії описується 2 началом тд-ки.

Стан системи визначається двома видами рівнянь стану. Їх існування витікає з 2го постулату тд-ки. Ф-ція стану визначається повним диференціалом , а ф-ція процесу – зміною , наприклад . Ел-нтарна робота:

де

- узагальнена тд. сила ( );

- тд. к-ната ( ).

Якщо на систему діє багато сил (система знаходиться під тиском і у ел. полі ), то робота дорівнює:

2. Другий постулат термодинаміки. Рівняння стану, їх виведення для ід. Газу і парамагнетика.

Якщо система задається внутр. енергією, то ї стан задається таким чином:

і таке рівняння наз-ть калорічним рівнянням стану.

Якщо стан системи задається тд. силами, то по 2му постулату:

- термічне рівняння

Кількість цих рівнянь дорівнює кількості тд. сил. Для того, щоб визначити тд. стан системи, треба задати рівняння стану. Розглянемо систему (на неї діє , параметрами стану є ). Маємо рівняння стану:

і термічне рівняння:

Стан системи описується 2ма рівняннями. Якщо газ ідеальний, то для одного моля:

3. Перше начало термодинаміки. Робота, енергія, теплота.

Якщо система ізольована, то її енергія не змінюється. 1 начало тд-ки:

де - дві форми енергії.

Формули для роботи, теплоти, енергії:

4. Друге начало термодинаміки для квазістат. Процесів. Мат. Обґрунтування існування ентропії.

Квазістатичні процеси ідуть так повільно, що в деякий інтервал часу можна вважати, що деяка фіз. вел-на є сталою. Біля кожного стану рівноважної однорідної системи будуть існувати такі стани, які недосяжні адіабатично. Нехай є стани 1 і 2:

За 1шим началом тд-ки (до переходу 1-2):

Після адіабатичного переходу 1-2:

Складемо ці рівняння:

Робота була виконана без компенсації, а цього бути не може. Отже із стану 2 в 1 адіабатично перейти не можна. Робимо висновок, що існує деяка нова ф-ція стану:

- ентропія, де

- емпірична темп-ра, - зовн. параметри, - параметри стану. В нашому процесі .

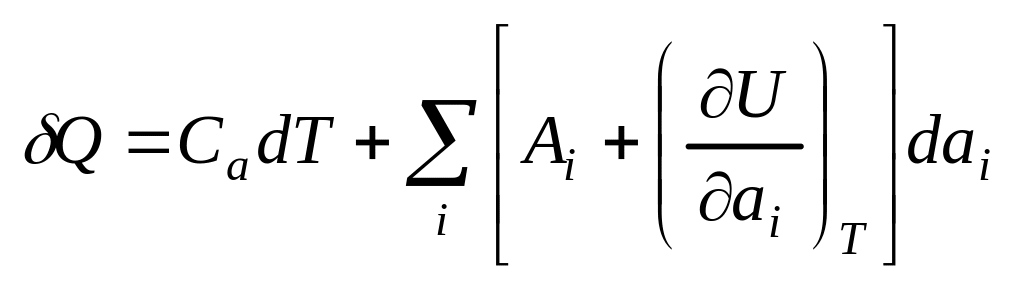
В стані 1 , в стані 2 , тобто перейти з стану 2 в 1 при неможливо. при адіабатному процесі .

і , і залежать від сукупності параметрів, тобто . Вони одночасно дорівнюють нулю в адіабатному процесі.

де

- ф-ція стану, - ф-ція процесу.

З мат. аналізу відомо, що якщо ф-ція не є повним диференціалом, то її можна зробити повним диференціалом. Якщо виберемо такй множник, що залежить лише від : , то можна показати, що вигляд функції буде різним в залежності від того, яку емпіричну температуру ми виберемо. Для різних емпіричних температур функції матимуть різний вигляд але абсолютна температура, що відповідає цим емпіричним, є однією і тією самою.

Якщо , то функція стану зветься ентропією.

- визначення 2-го начала термодинаміки.

, де Т- термодинамічна сила, S-координата. . Якщо процес адіабатичний то

Тобто при квазістатичних процесах в ізольваній системі не змінюється.

- формула для обчислення ентропії, (1)

і (2) – стани.

2-м началом термодинаміки обчислюємо абсолютне значення , а її зміну. Для того, щоб знайти абсолютне значення , треба ввести деякий детермінований стан.(тобто стан в якому ми знаємо значення ). Таким чином є стан біля абсолютного нуля ( ). Тоді інтеграл береться від (0).

З принципу адіабатичної недосяжності отримали, що диференційну форму можна зробити повним диференціалом діленням на інтегруючий дільник .Покажемо, що серед усіх існують такий, що залежить лише від емпіричної температури t, тобто , і визначає ентропію системи, причому головне значення не залежить від вибору .

Існування . Нехай є дві підсистеми, що знаходяться в тепловій рівновазі. Стан 1-ї визначається параметрами

другої всієї системи в цілому –параметрами . Нехай в деякому рівноважному процесі системам надали теплоти і , (1)

Усі ці елементи головні: , де - інтегруючі дільники; і - функції стану систем, їх можна взяти в якості незалежних змінних кожної з систем, наприклад замість і :

(3)

З (1) і (2) маємо (4)

З (3) і (4) маємо

З 3 – ї і 4 – ї рівності маємо

Оскільки не залежить від , а від то з рівностей 5-8 маємо , що не залежить від і , від , від .Тоді

Функції і , довільні. Можемо підібрати функції так, що

є однаковим для всіх систем, що знаходяться в тепл. рівновазі. Функція , що визначається рівнянням називається ентропією 1-ї системи, відповідно , що

Ввиводиться з рівняння