
- •Лабораторная работа № 2 определение параметров типовых динамических звеньев по их частотным характеристикам
- •Теоретическая часть
- •Подставляя уравнения (2) в (1), получим
- •Апериодическое (инерционное) звено
- •Дифференцирующее звено первого порядка
- •Для схемы рис.7а
- •Колебательное звено
- •Лабораторное задание
- •Описание лабораторного стенда
- •Порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •Литература
Апериодическое (инерционное) звено
Дифференциальное уравнение и передаточная функция апериодического звена имеют вид:

На основании передаточной функции можно записать выражение для частотной характеристики
![]() ,
,
или
![]() .
.
Следовательно,

На рис.1 изображена АФХ апериодического звена.

Рис. 1. АФХ апериодического звена.
Пунктирная линия соответствует отрицательным значениям частоты. Характеристика представляет собой окружность, диаметр которой равен статическому коэффициенту усиления (в данном случае – единице). Каждой точке характеристики соответствует определенное значение частоты колебаний.
Логарифмическая амплитудно-частотная характеристика:
![]() .
.
При
низких частотах, когда Т<<1
или <<1/Т,
можно считать, что
![]() .
Это означает, что при низких частотах
<<
Т/1 и L()
имеет вид прямой линии, совпадающей с
осью частот.
.
Это означает, что при низких частотах
<<
Т/1 и L()
имеет вид прямой линии, совпадающей с
осью частот.
При высоких частотах, когда Т>>1, т.е. >>1/Т ,
![]() .
.
Отсюда следует, что при высоких частотах L() изображается наклонной прямой с отрицательным наклоном, который можно определить следующим образом.
Для любого значения частоты =1 имеем
![]()
При десятикратном увеличении частоты, т.е. =101, что соответствует в логарифмическом масштабе изменению частоты на одну декаду,
![]()
Следовательно, приращение амплитуды в интервале, равен одной декаде
![]() .
.
таким образом, наклон прямой линии при высоких частотах составляет 20 дб/дек или 6 дб/окт.
![]() .
.
Суммируя L1() и L2(), получим ЛАЧХ L() апериодического звена (рис.2).
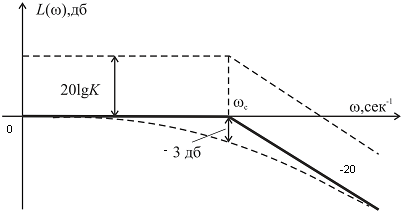
Рис. 2. ЛАЧХ апериодического звена.
Для того, чтобы построить асимптотическую ЛАЧХ апериодического звена, надо провести прямую L1() вдоль оси частот до частоты с=1/Т и из этой точки – прямую L2() с наклоном в 20 дб/дек. Частота с , в которой сопрягаются два отрезка характеристики, называется сопрягающей частотой. В случае, если апериодическое звено имеет коэффициент передачи К, т.е. числитель передаточной функции не I, то вся логарифмическая характеристика сместится параллельно оси ординат на величину 20lgК (рис.2).
Асимптотическая ЛАЧХ является приближенной характеристикой и наибольшее отклонение ее от действительной в точке с составляет 3 дб (пунктирная линия на рисунке изображает точную характеристику).
Для фазовой характеристики логарифмический масштаб используется только по оси частот, поэтому выражение для нее остается прежним, т.е.:
()=-arctgT.
Фазовая характеристика изображена на рис.3. Ее обычно строят на одном графике с амплитудной характеристике:

Рис. 3. Фазовая характеристика апериодического звена.
При построении фазовой характеристики апериодического звена можно использовать следующие данные:
Т |
0,1 |
0,2 |
0,5 |
1 |
2 |
5 |
10 |
() |
-6 |
-11,3 |
-26,6 |
-45 |
-78,7 |
-63,4 |
-84 |
Примером апериодического звена является RC-контур (рис.4).

Рис. 4. Апериодическое звено на RC-элементах.
Входное и выходное напряжение в этой схеме связаны следующим соотношением:
 .
.
Обозначая RC = T, можем записать окончательно передаточную функцию:
![]()
Заменяя р на j в передаточной функции, получаем выражение для частотной АФХ
.
