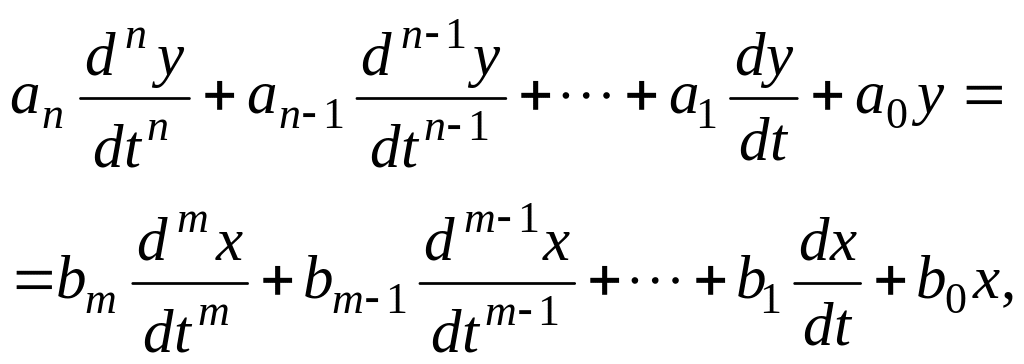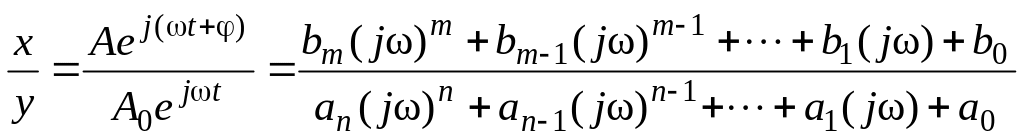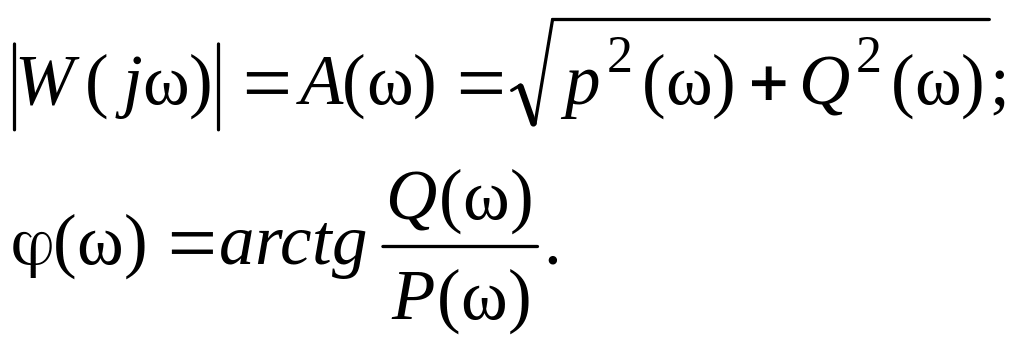Лабораторная работа № 2 определение параметров типовых динамических звеньев по их частотным характеристикам

Цель работы:	Экспериментальное определение частотных характеристик типовых динамических звеньев и исследование влияния на них параметров звеньев.
Оборудование:	Лабораторный стенд. Генератор синусоидальных колебаний типа Г3-111. Ламповый вольтметр В3-6. Фазометр Ф2-1.
Продолжительность работы: 4 часа.

Теоретическая часть

Линейная система автоматического управления, отдельное звено или элемент могут быть описаны дифференциальным уравнением, связывающим выходную координату с входной

(1)

где х(t) и y(t) – входной и выходной сигналы.

Если предположить, что на вход рассматриваемой системы (звена) подан синусоидальный сигнал y(t) с частотой , то на выходе устойчивой системы по истечении достаточно большого промежутка времени после затухания свободных составляющих процесса установится периодическое движение той же частоты , но с другими амплитудами и фазой.

При постоянной амплитуде входного сигнала амплитуда А и фаза  выходного сигнала в линейной системе определяются лишь частотой входного сигнала, т.е. А = А() и  = ().

Выразим гармонические функции х(t) и y(t) в комплексной форме:

(2)

Подставляя уравнения (2) в (1), получим

(3)

Из уравнения (3)

Обозначая правую часть через W(j) и, проводя сокращение в левой части на e ^jt, будем иметь:

(4)

Комплексная функция частоты W(j) называется частотной амплитудно-фазовой характеристикой (АФК) (комплексным коэффициентом передачи, частотной передаточной функцией). Модуль АФК равен отношению А/А₀ амплитуды выходной координаты у к амплитуде воздействия х и является амплитудно-частотной характеристикой А(). Он показывает зависимость изменения амплитуды выходного сигнала от частоты входного. Аргумент () показывает сдвиг по фазе выходного сигнала относительно входного и служит фазо-частотной характеристикой.

Частотной АФХ системы называется отношение преобразования Фурье выходной величины к преобразованию Фурье входной величины.

Таким образом, если заданы амплитуда А₀ и частота  входного сигнала, то с помощью АФХ легко найти амплитуду А и фазу  установившегося периодического изменения выходной величины х_вых. Если дифференциальное уравнение системы задано, то функция W(j) определяется по формуле:

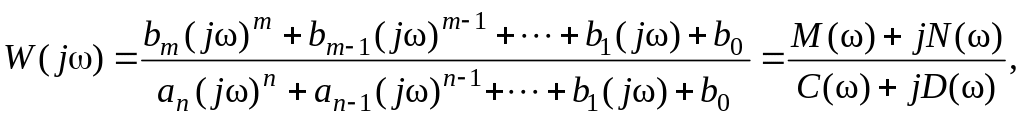
где

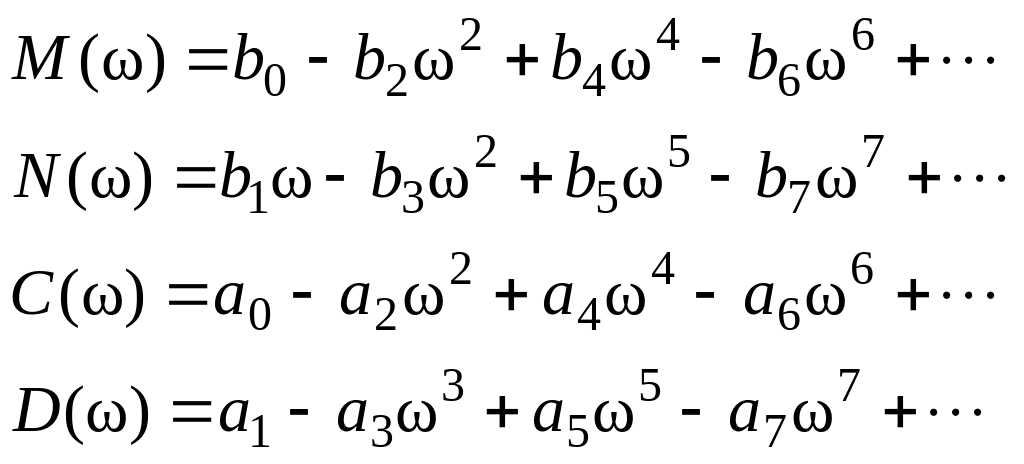
Освобождаясь от мнимой части в знаменателе, получаем

.

Величины Р() и Q() называются соответственно вещественной и мнимой частотными характеристиками систем:

(5)

Модуль и фаза частотной характеристики определяются следующим образом:

(6)

АФХ можно построить, зная ее аналитическое выражение по формулам (5) или (6) и задавая различные значения . Для реальных систем и звеньев ее можно также представить экспериментально, задавая на входе звена гармонический сигнал постоянной амплитуды и различной частоты.

Для каждого значения частоты отношение выходной амплитуды к входной будет значением модуля W(j). Фаза выходного сигнала относительно входного измеряется фазометром. Для ряда значений А() и () можно построить годограф частотной характеристики, т.е. траекторию конца вектора W(j).

Амплитудную и фазовую частотные характеристики удобно строить в логарифмическом масштабе, что значительно упрощает как вычисление, так и построение характеристик особенно для сложных систем, состоящих из последовательного соединения простых звеньев. Логарифмический масштаб позволяет упрощенно изображать амплитудные частотные характеристики в виде асимптотических логарифмических характеристики (ЛАХ), представляющих собой совокупность отрезков ломаных линий.

По оси абсцисс откладывается частота в логарифмическом масштабе. За единицу длины по оси абсцисс принимают логарифмические единицы – октаву или декаду. Отрезок оси lg, равный одной октаве, соответствует удвоению частоты; отрезок в одну декаду – изменению  в десять раз.

По оси ординат для фазовой характеристики откладываются градусы, а для амплитудной – децибелы (величина 20 lgА()).