Распределение лучистой энергии в фокальной плоскости реального концентратора

В настоящее время используются две статистические модели процесса отражения падающих на концентратор потоков лучис­той энергии. Одна из них полагает равенство угловых размеров падающего и отраженного пучков и основывается на предполо­жении о нормальном распределении локальных угловых откло­нений отражающей поверхности от идеальной. Для мериди-альных угловых отклонений осей отраженных пучков этот закон записывается в виде

где — угол, характеризующий отклонение оси отраженного

пучка от точного направления к фокусу, рад; —плотность вероятности случайных значений угла ; — среднеквадратическая ошибка (стандарт) , рад.

Величина связана со среднеквадратической угловой ошиб­кой поверхности концентратора соотношением = 2 , кото­рое вытекает из закона зеркального отражения.

Вторая модель имеет более условный характер и основывает­ся на следующих допущениях. Полагается, что оси всех отражен­ных пучков имеют направления, соответствующие зеркальному отражению от поверхности геометрически идеального концентра­тора, а энергия в каждом пучке распределена пропорционально плотности вероятности угловых отклонений луча от оси пучка при условии нормального закона распределения этих от­клонений. Указанный закон для данного случая согласно можно представить в виде

где — текущий угол отклонения луча от оси пучка, рад; — мера точности , 1/рад.

Распределяя энергию, заключенную в отраженном пучке, пропорционально плотности вероятности , получим следую­щее выражение для энергии в направлении отдельного луча:

где dN_отр — определяется уравнением

После преобразований уравнение приобретает вид

Если выразить площадь проекции элементарной площадки па-

раболоидного отражателя (рис. 4) в полярных координатах

то уравнение можно записать в виде

С ледует заметить, что уравнение относится к частному случаю параболоидного концентратора, а уравнение применимо к концентраторам любых форм.

Рис. 4. К определению ха­рактеристики фокального рас­пределения лучистой энергии

Перейдем далее к определению важнейшей характеристики процес­са концентрации лучистой энергии — распределению энергии в фокальной плоскости. Указанная характеристи­ка позволяет выбрать рациональные размеры приемного устройства и в конечном счете осуществить согла­сование параметров всей системы «концентратор — приемник». Опре­деление характеристики фокального распределения лучистых потоков может проводиться различными экс­периментальными или теоретически­ми методами. Однако для практики инженерных расчетов наибольший интерес представляет аналитичес­кие зависимости, позволяющие с достаточной степенью точности опи­сывать это распределение. При оп­ределении плотности облучения в произвольной точке фокальной плоскости параболоидный кон­центратор можно рассматривать как вторичный излучатель, со­стоящий из множества бесконечно малых элементов dS_K, излуча­ющих по закону, выраженному уравнением. Тогда в про­извольной точке Р (см. рис. 4), лежащей на окружности ра­диуса r в фокальной плоскости (центр окружности совпадает с фокусом F) , плотность лучистого потока, исходящего от пло­щадки dS_K, определится как

Подставляя в выражение значение и полагая, что вследствие малости угла справедливы равенства и , получим следующее уравнение для :

Для определения полной плотности лучистого потока в точ­ке Р, т. е. плотности, создаваемой всеми элементами отражате­ля, излучение от которых попадает в эту точку, уравнение необходимо проинтегрировать по всей отражающей поверх­ности

Текущее значение угла определяется выражением

При каждом фиксированном значении U угол изменяется от до , которые соответственно равны

Учитывая малость угла , примем = ^max, имея, однако, в виду, что это допущение должно привести к занижению расчет­ных значений плотности лучистых потоков в фокальной плоско­сти. Считая теперь, что от не зависит, выражение мо­жем преобразовать к виду

Поскольку функция в интервале [0, U_K] не отрицательна и монотонно возрастает по U, то на основании вто­рой теоремы о среднем можем записать

где

Примем = 0, что будет соответствовать максимальному зна­чению интеграла. Это допущение должно определенным образом компенсировать предыдущее ( = ^max). После интегрирования и подстановки получим

или

Где - максимальная плотность отраженно­го излучения в центре (r = 0) фокального пятна;

— геометрический параметр концентратора.

Из формулы видно, что резко очерченных границ фо­кального пятна у реального отражателя не существует, так как при . Но из-за резкого спада по r основная часть сконцентрированного излучения ( ) локализуется внутри круга ограниченного радиуса, который можно считать радиусом фокального пятна. Осредняя по этой площади, определяют среднюю плотность отраженного излучения:

где — допустимый по условию ограничения максимальных потерь сконцентрированного излучения радиус фокального пятна.

На рис. 5 в безразмерных параметрах даны типичные кри­вые распределения энергии в фокальной плоскости для отража­телей с различными значениями параметра . Характеристики, полученные по формуле, хорошо согласуются с экспери­ментальными данными.

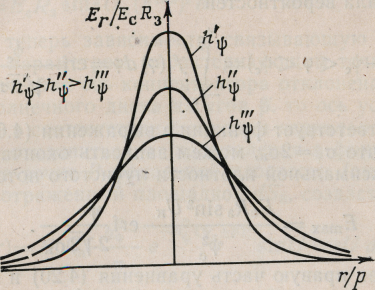
Рис. 5. Распределение энергии в фокаль­ной плоскости

Если считать, что угловые размеры падающего и отраженных пучков одинаковы и рассматривать геометрически идеальный отражатель, то среднюю величину плотности лучистого потока, переносимого в фокальную плос­кость от производной площадки dS_K, можно представить в виде

где - площадь эллипса, образованного при пересечении отраженного пучка с фокальной плоскостью.

В фокусе плотность отраженного потока определится интегри­рованием уравнения по всей поверхности концентратора:

В реальном случае при условии, что оси отраженных пучков отклоняются в соответствии с законом нормального распределения, получим следующее выражение для максимальной плотности лучистого потока в центре фокальной плоскости:

где - вероятность того, что отклонение осей от­раженных пучков от идеального направления в фокус зеркала превысит (в противном случае отраженный пучок не попа­дет в фокус).

Учитывая, что , можем записать окончательное выра­жение для максимальной плотности лучистого потока в виде

Приравнивая правую часть уравнения и значение , получим искомое выражение для

которое позволяет установить связь между и .

Таким образом, зная на основании данных аберрационных ис­пытаний для отражателей того или иного типа, можно найти с помощью уравнения производить оценки распре­деления сконцентрированной в фокальной плоскости энергии.

Все приведенные выше зависимости получены в предположе­нии, что отражатель-концентратор точно сориентирован в на­правлении Солнца. В реальных условиях работы СТЭУ вследст­вие влияния целого ряда факторов оптическая ось концентратора постоянно отклоняется от направления в центр солнечного диска возвращается в прицельное положение с помощью системы ориентации. Таким образом, оптическая ось совершает непрерыв­ные колебания относительно точного (прицельного) направле­ния В результате эффективная концентрирующая способность отражателя снижается, что приводит также к уменьшению к. п. д. системы «концентратор — приемник». Можно счи­тать, что неточность углового слежения оказывает в этом смысле такое же влияние, как и неточность геометрии отражающей поверхности концентратора.

Следовательно, с определенной степенью погрешности можно допустить, что среднее за период колебания состояние Данной системы в динамическом режиме слежения эквивалентно прицельному статическому состоянию такой же системы, но с «кажущимся» (динамическим) параметром точности меньшим, чем . Распределение плотности лучистых потоков в фокальной плоскости концентратора такой системы по аналогии будет описываться уравнением

.

Сопоставление технических характеристик

В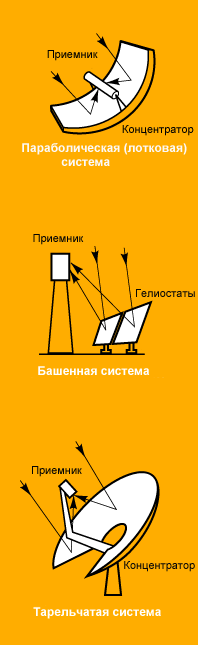 таблице сведены ключевые характеристики трех вариантов солнечной тепловой электрогенерации. Башни и параболоцилиндрические концентраторы оптимально работают в составе крупных, соединенных с сетью электростанций мощностью 30-200 МВт, тогда как системы тарельчатого типа состоят из модулей и могут использоваться как в автономных установках, так и группами общей мощностью в несколько мегаватт. Параболоцилиндрические установки - на сегодня наиболее развитая из солнечных энергетических технологий и именно они, вероятно, будут использоваться в ближайшей перспективе. Электростанции башенного типа, благодаря своей эффективной теплоаккумулирующей способности, также могут стать солнечными электростанциями недалекого будущего. Модульный характер "тарелок" позволяет использовать их в небольших установках. Башни и "тарелки" позволяют достичь более высоких значений КПД превращения солнечной энергии в электрическую при меньшей стоимости, чем у параболических концентраторов. Однако, остается неясным, смогут ли эти технологии достичь необходимого снижения капитальных затрат. Параболические концентраторы в настоящее время - уже апробированная технология, ожидающая своего шанса на совершенствование. Башенные электростанции нуждаются в демонстрации эффективности и эксплуатационной надежности технологии расплавленных солей при использовании недорогих гелиостатов. Для систем тарельчатого типа необходимо создание хотя бы одного коммерческого двигателя и разработка недорого концентратора.