РОСЖЕЛДОР
Государственное образовательное учреждение
высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(РГУПС)
Н.П. Воронова, А.В. Безуглый
РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ
Учебно-методическое пособие
к расчетно-графической работе №5 по курсу
«Теоретические основы электротехники»
Ростов-на-Дону
2009
У
ДК
Воронова, Н.П.
Расчет трехфазной цепи : учебно-методическое пособие к расчетно-графической работе № 2 / Н.П. Воронова, А.В. Безуглый ; Рост. гос. ун-т путей сообщения. – Ростов н/Д, 2009. –11 с. : ил. Библ. : 2 назв.
Составлено в соответствии с программой курса «Теоретические основы электротехники» и содержит различные варианты задания с краткими методическими указаниями.
Предназначено для студентов электротехнических специальностей 190401, 140601, 140104,190402).
Работа одобрена к изданию кафедрой ТОЭ РГУПС
Рецензент: канд. техн. наук, доц. П.А. Бодров (РГУПС)
© Воронова Н.П., Безуглый А.В. 2009
© Ростовский государственный университет
путей сообщения, 2009
Расчетное задание
Симметричный трехфазный генератор, обмотки которого соединены треугольником, питает равномерную нагрузку, соединенную треугольником (рис. 1).
Рис. 1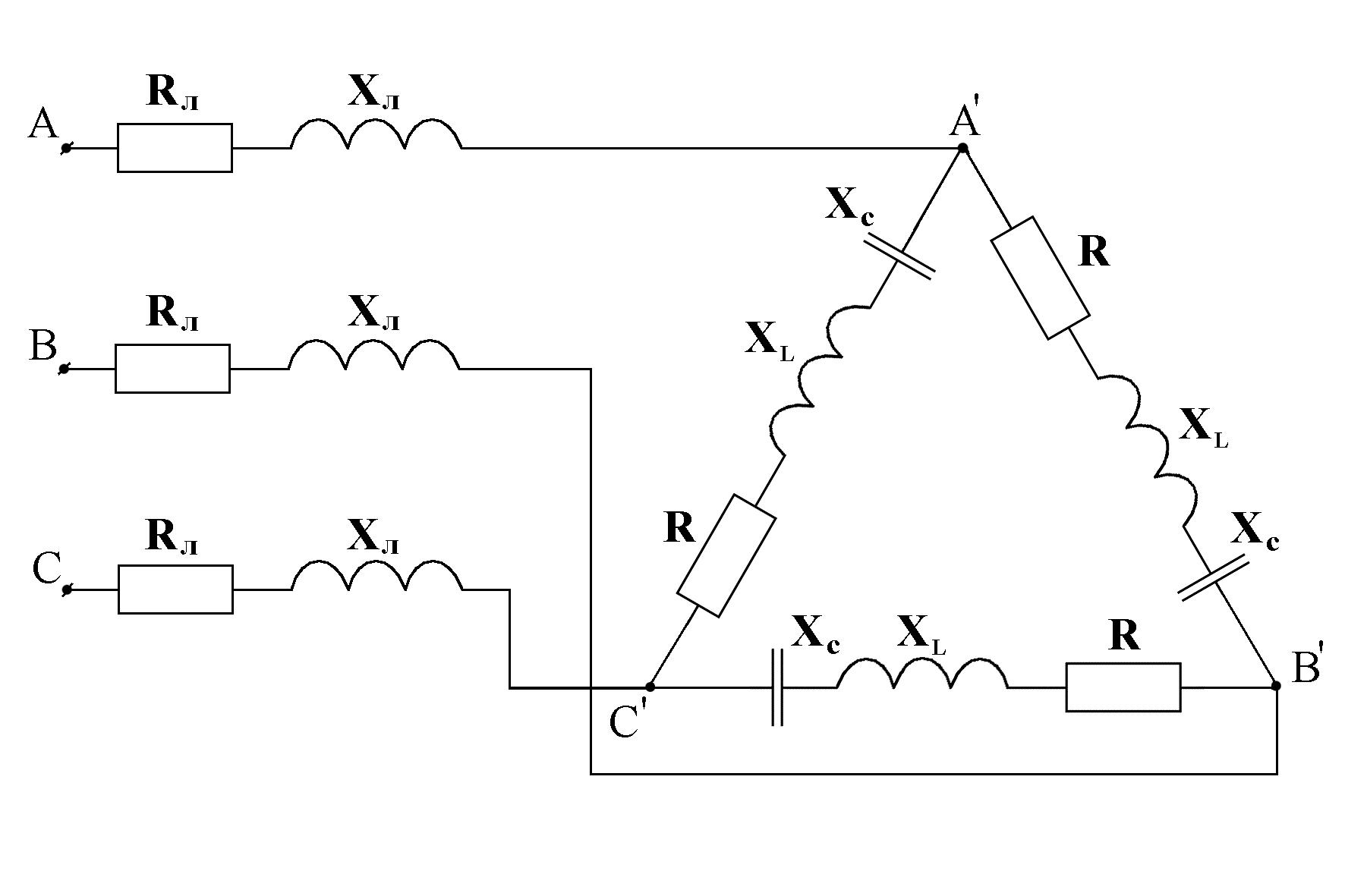
Напряжение фазы генератора UAB приведено в табл. 1, сопротивление фаз нагрузки R, XL, XC, и сопротивление линейных проводов Rл, Xл – в табл. 2, а в табл. 3 указаны фазы, в которых произошло короткое замыкание на активном сопротивлении.
Напряжение фазы генератора, в Таблица 1
Первая цифра варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
UAB |
220 |
173 |
346 |
380 |
220 |
173 |
346 |
380 |
220 |
346 |
Сопротивление фаз нагрузки и линейных проводов, Ом Таблица 2
Вторая цифра варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
RЛ |
10 |
0 |
0 |
4 |
3 |
5 |
3 |
9 |
12 |
15 |
XЛ |
3 |
4 |
6 |
8 |
0 |
0 |
7 |
10 |
9 |
10 |
R |
20 |
18 |
10 |
12 |
15 |
16 |
20 |
22 |
25 |
30 |
XL |
5 |
15 |
8 |
0 |
10 |
0 |
12 |
10 |
0 |
20 |
XC |
15 |
5 |
0 |
6 |
2 |
10 |
2 |
0 |
15 |
5 |
Фазы короткого замыкания Таблица 3
Третья цифра варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
Короткое замыкание на фазе |
АВ |
АВ |
ВС |
СА |
АВ |
СА |
ВС |
СА |
АВ |
ВС |
ТРЕБУЕТСЯ:
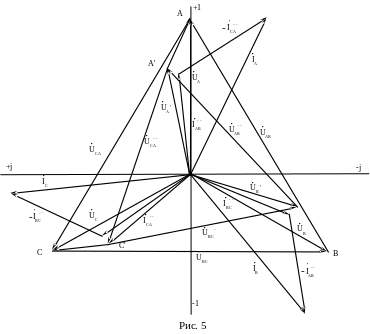
Рассчитать фазные токи нагрузки, линейные токи, напряжения на фазах нагрузки, активную мощность, развиваемую генератором и потребляемую нагрузкой, КПД системы и начертить топографическую диаграмму.
Произвести расчеты и построения по п. 1, считая, что произошло короткое замыкание на активном сопротивлении фазы, указанной в табл.3.
Найти аналитическим и графическим путем симметричные составляющие несимметричных линейных токов, полученных при расчете по п.2.
Исследовать режим работы схемы при изменении нагрузки фазы
,
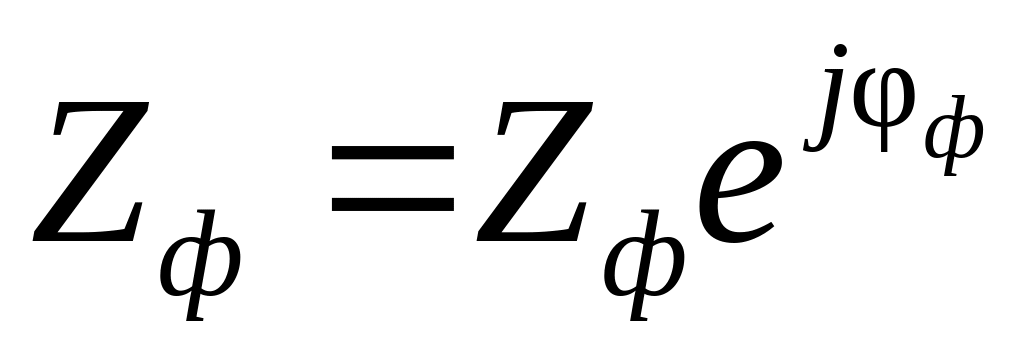указанной в табл.3, от 0 до ,
считая, что модуль нагрузки меняется
Zн = var,
а фаза постоянна
=
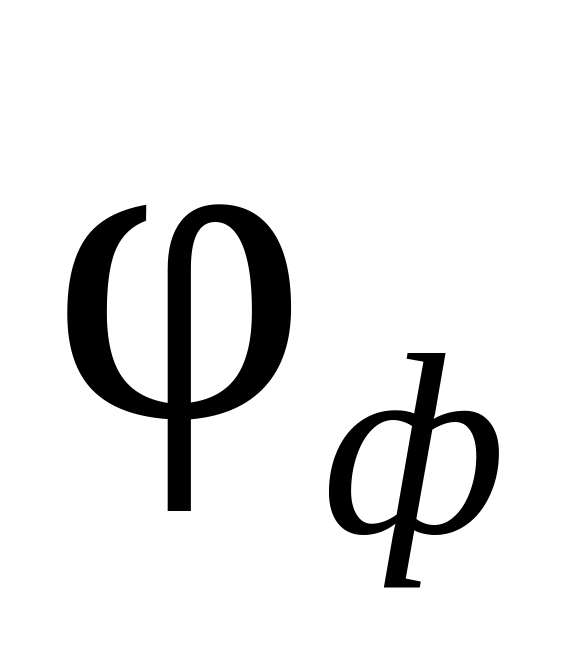const. По результатам
расчетов построить на топографической
диаграмме путь смещения нулевой точки
нагрузки.
Указание: исследования по п. 4 рекомендуется вести с использованием ЭВМ.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Симметричный режим
В симметричной трехфазной цепи комплексные сопротивления составляющих ее фаз одинаковы.
При соединении треугольником линейные и фазные напряжения и токи связаны соотношением:
;
.
Мощность в симметричной трехфазной системе составляет:
В задании к расчетно-графической работе предполагается, что генератор и приемник соединены треугольником. При наличии сопротивления в линейных проводах расчет следует начать с преобразования треугольника приемника в эквивалентную звезду.
Расчеты рекомендуется производить в следующем порядке:
О
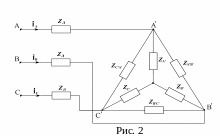пределить
сопротивления эквивалентной звезды
(рис. 2).
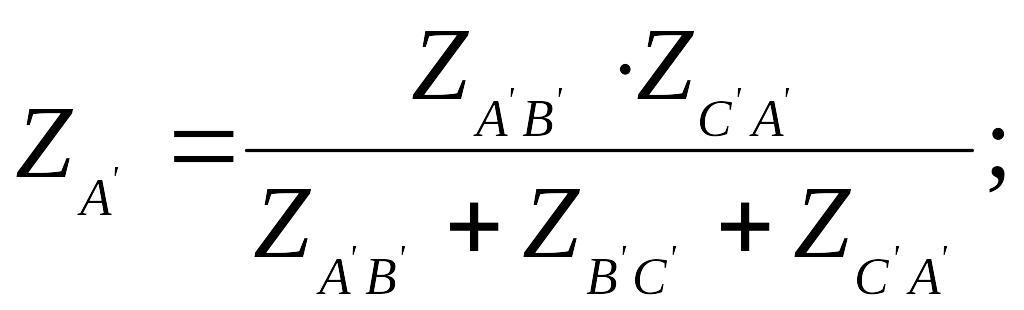
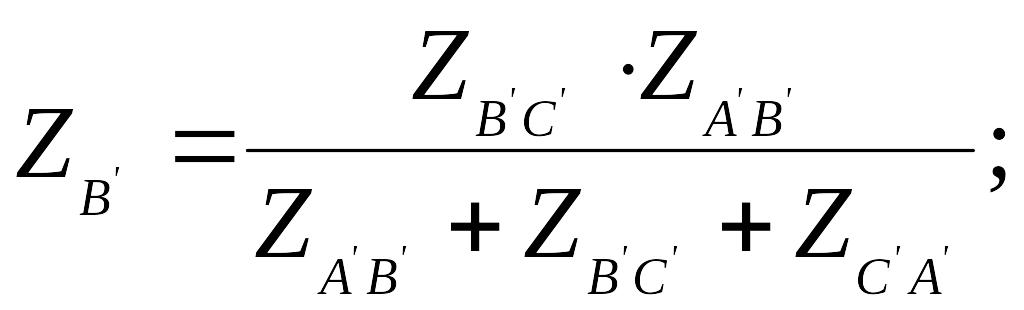
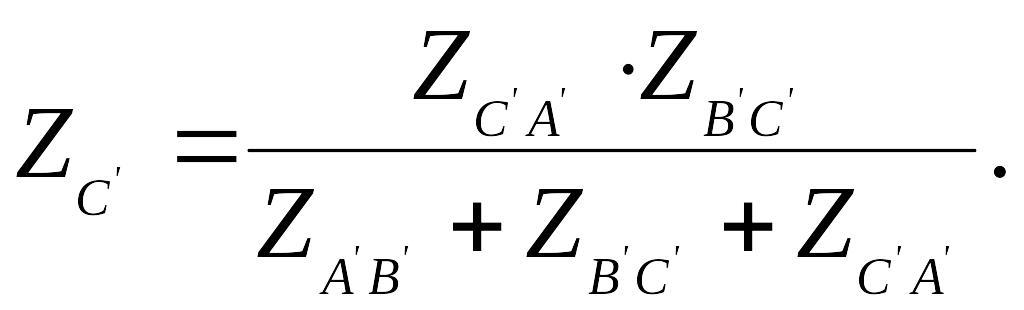
В случае симметричной системы
,
а
.
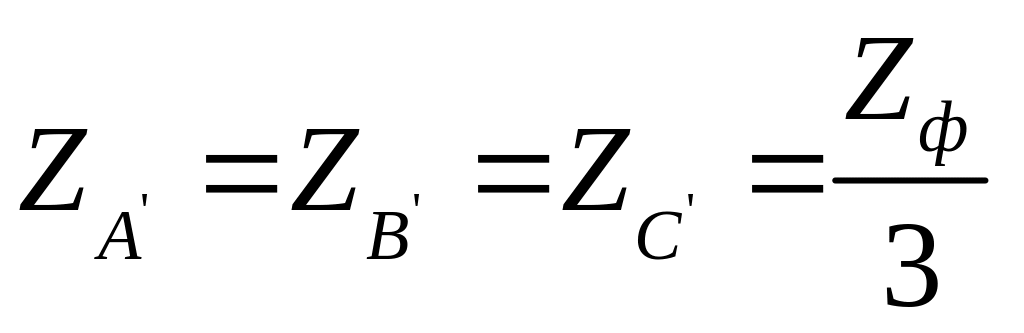Вычислить линейные токи
Фазное напряжение
эквивалентной звезды
.
Принимаем
,
тогда
и
.
В общем виде токи в линиях
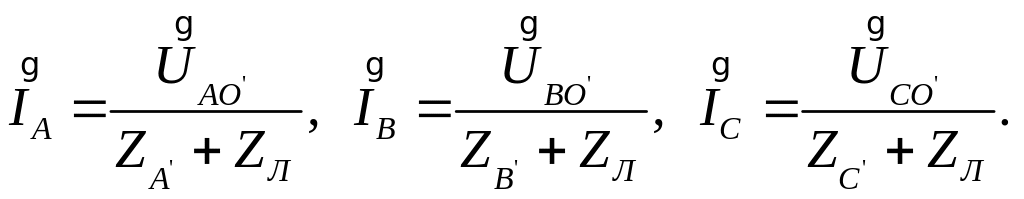
Для симметричного режима
Определить напряжение фаз треугольника
или
Найти фазные токи треугольника
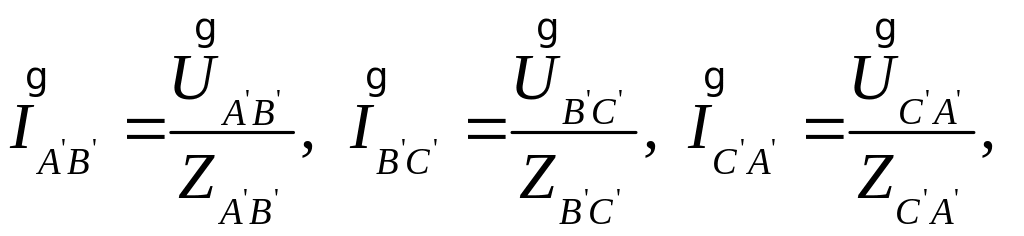
или
Для расчета кпд системы следует определить мощности генератора
,
и приемника
.
Коэффициент полезного действия трехфазной системы
.
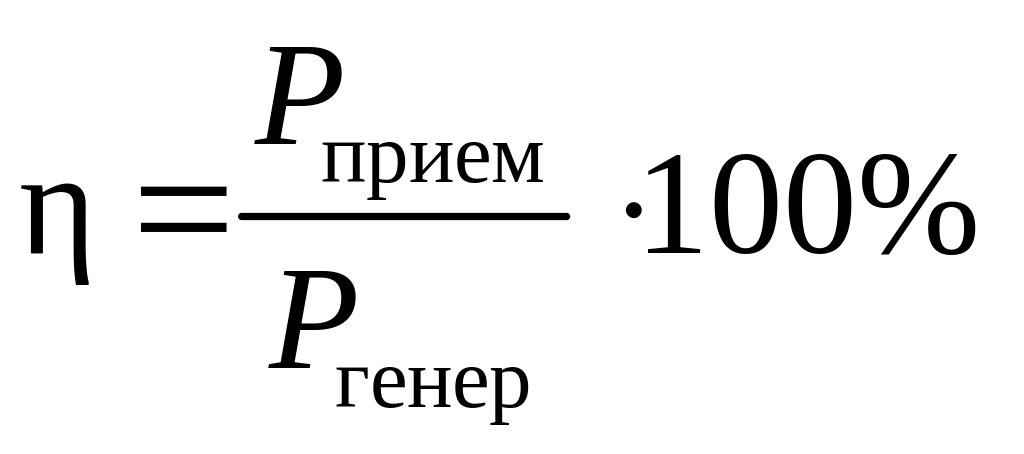Несимметричный режим
В несимметричной
трехфазной цепи комплексные сопротивления
составляющих ее фаз неодинаковы. Расчет
следует начинать с определения
сопротивлений эквивалентной звезды
(расчетные формулы приведены в подразделе
2.1).
Напряжение
между
нулевыми точками приемника и генератора
рассчитывается по формуле:
;
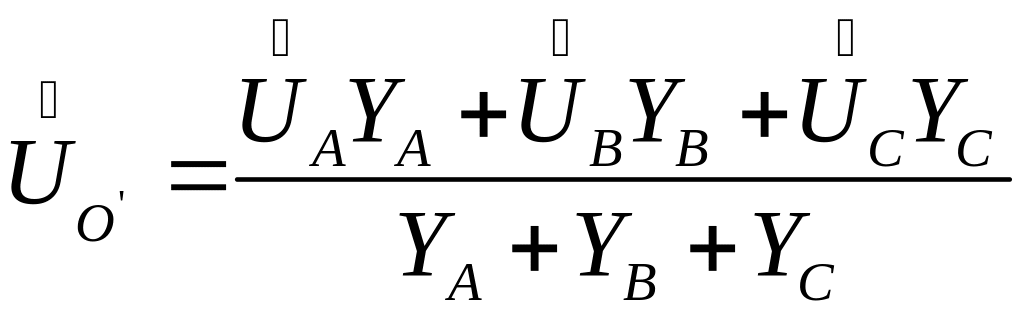где:
–
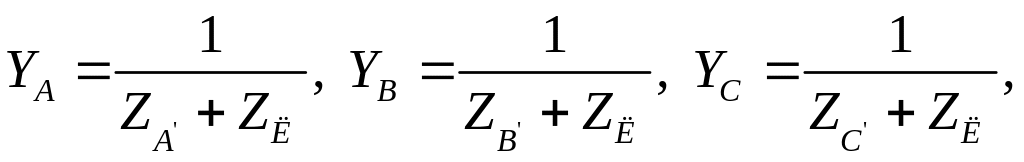
фазные напряжения
генератора.
Токи в линиях рассчитываются по формулам
Напряжения фаз треугольника составят
Сумма комплексных линейных напряжений равна нулю
Фазные токи треугольника
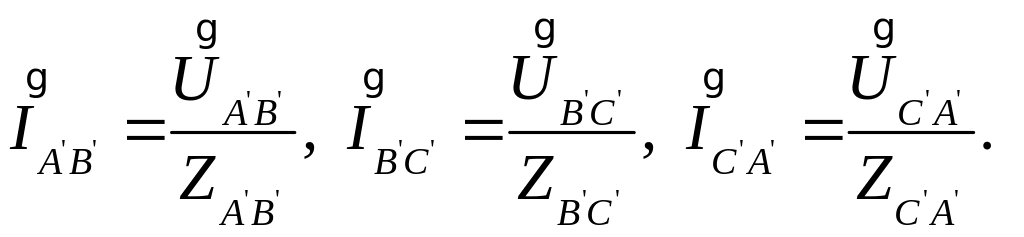
Для расчета коэффициента полезного действия системы необходимо определить мощности генератора и приемника
.
ПРИМЕР РАСЧЕТА
Рассчитать схему, представленную на рис. 3.
Д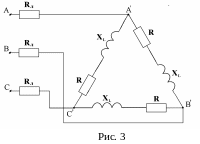
ано:
Rл = 3 Ом;
R = 15 Ом;
XL = 10 Ом;
=
300 В.
Короткое замыкание произошло в фазе АВ.
В данном примере приведены подробные расчеты для того, чтобы показать наиболее рациональный путь вычислений.
Симметричный режим
П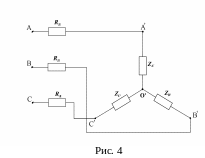
ри
наличии сопротивления линейных проводов
рассчитать схему можно только после
преобразования треугольника сопротивлений
нагрузки в эквивалентную звезду. При
этом схема приобретает вид, изображенный
на рис. 4.
Сопротивления фаз эквивалентной симметричной звезды
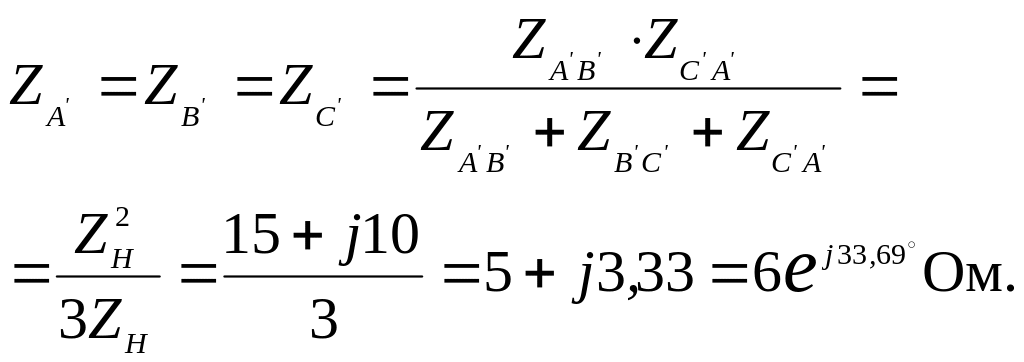
Ввиду полной симметрии системы напряжение между нулевыми точками генератора и нагрузки равно нулю. Каждую фазу можно рассматривать независимо от других фаз. Так, например, ток в фазе А может быть найден на основании закона Ома. В расчете примем
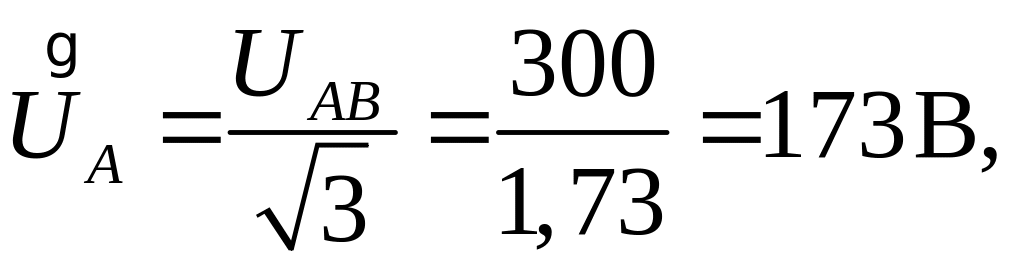
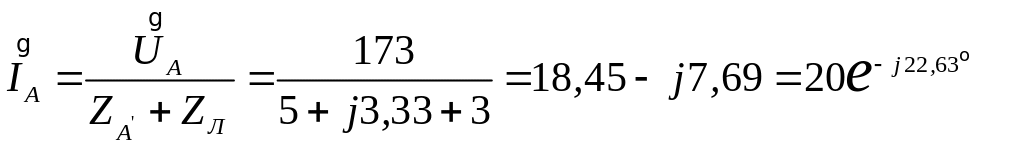А.
Напряжения и токи в других фазах сдвинуты соответственно на –120 и +120
А,
А.
Проверка
.
Фазные напряжения на эквивалентной звезде
В,
В,
В.
Линейные напряжения эквивалентной звезды и исходного треугольника
В,
В,
В.
Падения напряжения в линии
А,
А,
А.
Проверка
.
Фазные токи нагрузки (исходного треугольника)
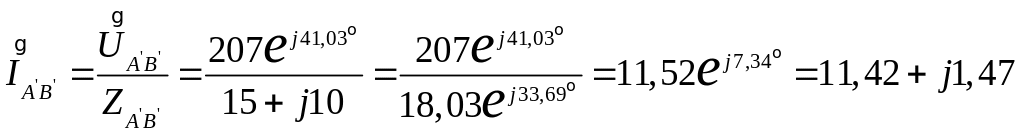A,
A,
A.
Проверка
.
Мощность, развиваемая генератором, составит
Вт,
Мощность в нагрузке
Коэффициент полезного действия системы
.
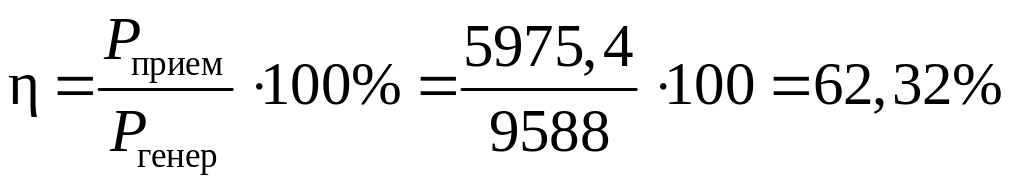Топографическая диаграмма симметричного режима представлена на рис. 5.
